Pytorch:深度学习中的Normalization
1.Normalization
深度学习中的Normalizaiton主要有以下几种方式:
- BatchNorm
- LayerNorm
- InstanceNorm
- GroupNorm
1.1.Normalization的意义
参考:ICS(internal covariate shift)问题详解
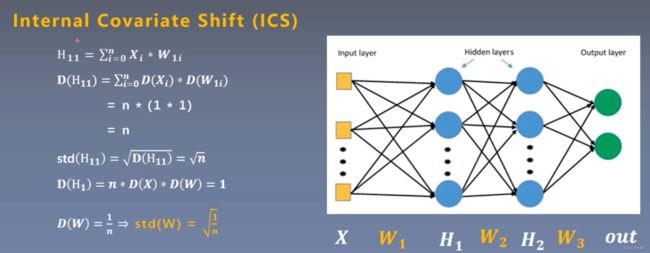
Normalization主要是解决ICS问题,我们常说深度学习神经网络学习到特征,其实学习的是一个样本数据中的数据分布,所以当训练数据和测试数据分布一致,效果是最好的。但是神经网络有多层,如果数据经过一层后都发生了数据分布的改变,就不能保证这个网络的高效性,这就是ICS问题,而深度学习中的Normalizaiton就是解决这个问题。
2.Batch Normalization
Batch Normalization:批标准化
batch normalizaiton 有m个样本的输入 x 1 − > x m x_1 -> x_m x1−>xm,同时又两个可学习参数 γ \gamma γ以及 β \beta β
- 第一步:在batch上求均值
- 第二步:在batch上求方差
- 第三步:做normalizing Transform
- 第四步:affine transfrom,做scale 和 shift,有两个可学习参数
为什么有第四步?
可以让模型容纳能力更强,模型自己判断是否对数据的分布进行改变。其实这就是算法关键之处:我们知道对网络某一层A的输出数据做归一化,然后送入网络下一层B,这样是会影响到本层网络A所学习到的特征的。打个比方,比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧,你强制把它给我归一化处理、标准差也限制在了1,把数据变换成分布于s函数的中间部分,这样就相当于我这一层网络所学习到的特征分布被你搞坏了,而引入这两个参数就可以解决这个问题。取一个特殊情况,如果γ等于标准差,βi等于均值,那激活值便于输入相同。
2.1.pytorch中的_BatchNorm
- nn.BatchNorm1d
- nn.BatchNorm2d
- nn.BatchNorm3d
以上3个实现类都继承自_BatchNorm
主要参数:
- num_features:一个样本的特征数,如下1d的图,就是5
- eps:分母修正项
- momentum:指数加权平均估计当前mean和var
- affine:是否需要affine transform
- track_running_stats:训练还是测试
主要属性:
- running_mean:均值
- running_var:方差
- weight:gamma
- bias:beta
2.1.1BatchNormxd中的数据特征
BatchNorm1d,BatchNorm2d,BatchNorm3d对数据的要求是怎么样,之间的特征有什么区别?
假设是对一个全连接的网络层的输出做batch norm,此层的输出有五个神经元五个特征,每个特征的维度是1,然后这个batch是3。
所以输入形式就是:3 * 5 * 1
4个主要参数的计算
如上图,现在有3个样本,每个样本有5个特征。先在第一个特征上求取均值方差,然后每个特征上都有自己的gamma,beta。具体验证见3.1.2通过pytorch验证BN计算方式
假设对2d卷积层的输出做batch norm,此卷积层输出的特征图是22大小,且一个层有3个卷积核,所以有3个特征图。同时也是有3个样本。
所以输入形式:33*(2*2)
假设对3d卷积层的输出做batch norm,此卷积层输出的特征图大小是322,有4个特征图。
所以输入形式:3 * 4 (3 2 * 2)
2.1.2 通过pytorch验证BN的计算方式
此部分通过1d的方式来验证BN的计算方式,batch中的数据也模拟成和上1d图一致。
代码以及运行结果验证如下:
"""
首先模拟出一个batch大小要经过BN计算的数据集
"""
batch_size = 3
num_features = 5
momentum = 0.3
features_shape = (1)
feature_map = torch.ones(features_shape) # 1D
feature_maps = torch.stack([feature_map*(i+1) for i in range(num_features)], dim=0) # 2D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 3D
print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))
""""
此priint输出如下:
input data:
tensor([[[1.],
[2.],
[3.],
[4.],
[5.]],
[[1.],
[2.],
[3.],
[4.],
[5.]],
[[1.],
[2.],
[3.],
[4.],
[5.]]]) shape is torch.Size([3, 5, 1])
可以看出模拟了一个batch,有3个样本,每个样本都是[1,2,3,4,5]
""""
# 创建一个BatchNorm1d
bn = nn.BatchNorm1d(num_features=num_features, momentum=momentum)
"""
模拟此BN层,经过了两个batch的计算。
"""
for i in range(2):
outputs = bn(feature_maps_bs)
print("\niteration:{}, running mean: {} ".format(i, bn.running_mean))
print("iteration:{}, running var:{} ".format(i, bn.running_var))
"""
第一个batch进入时,BN的结果如下
iteration:0, running mean: tensor([0.3000, 0.6000, 0.9000, 1.2000, 1.5000])
iteration:0, running var:tensor([0.7000, 0.7000, 0.7000, 0.7000, 0.7000])
以第一个维度特征的均值为例:3个样本在第一个维度特征上都是1,所以其均值是(1+1+1)/3 = 1
但是上面输出的结果为0.3,因为BN是一个加权计算,当前batch的权重的0.3,而这是此BN层第一次经过计算
则0.3 = 0.7 * pre_batch_mean + 0.3 * 1,而pre_batch_mean=0
即验证了BN是在一个batch上所有样本的每个维度特征上进行均值和方差计算。
"""
3.Layer Normalization
Layer Instance Group Normalization算法原理都和batch Normalization相同,不同之处在于求取mean和var的方式
- 起因:BN不适用与边长的网络,如RNN,一个batch中样本的特征数不一致。
- 思路:逐层计算均值和方差
- 注意事项:
- 不再有running_mean和running_var
- gamma和beta为逐元素的
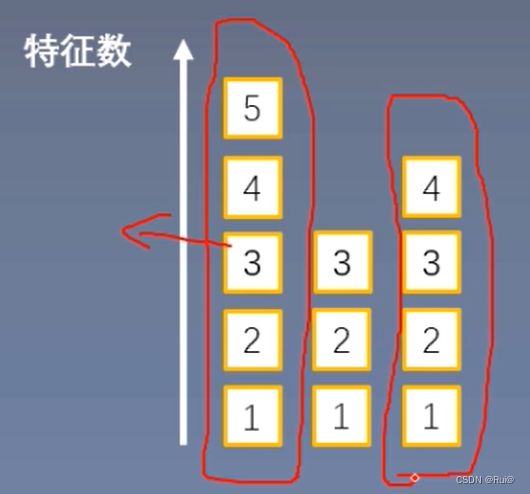
- 计算方式:对于batch中的样本,经过网络层输出后的神经元来计算均值和方差(即直接对样本中所有特征计算,如下图),并以此在每个样本中进行normalization.而不是BN中,对batch中所有样本的某个维度特征分别计算。同时每个神经元都有自己的可学习参数。
3.1.pytorch中Layer Normalizaiton
nn.LayerNorm
主要参数:
- normalized_shape:该层的形状(要接收数据的形状,不算batch_size)
- eps:分母修正项
- elementwise_affine:是否需要affine transform
3.2 通过pytorch验证其计算方式
以2D为例
代码以及结果展示推导如下:
"""
模拟出一个batch大小的要经过LN计算的数据集
"""
batch_size = 2
num_features = 3
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
print(feature_maps_bs.shape)
"""
此print输出如下:
torch.Size([2, 3, 2, 2])
模拟了一个batch,有2个样本,每个样本3个特征数(通道数),每个通道(特征图)大小是(2 * 2)
"""
"""
创建一个LN层,注意,此次第一个参数要传递,需要经过计算的样本形状大小,例如此处需要传递进(3,2,2)
本段代码用整个batch的形状下切片的方式传入样本的形状
也可ln = nn.LayerNorm([3, 2, 2])
"""
ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)
output = ln(feature_maps_bs)
print("Layer Normalization")
print(ln.weight.shape)
"""
此处输出:
torch.Size([3, 2, 2])
和样本一样大小,验证了LN中gamma和beat是逐元素的
"""
print(feature_maps_bs[0, ...])
"""
此处输出(第一个样本数据):
tensor([[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]])
"""
print(output[0, ...])
"""
此处输出LN后的结果:
tensor([[[-1.2247, -1.2247],
[-1.2247, -1.2247]],
[[ 0.0000, 0.0000],
[ 0.0000, 0.0000]],
[[ 1.2247, 1.2247],
[ 1.2247, 1.2247]]], grad_fn=)
LN中没有running_mean等属性,所以不能通过这个属性来验证其计算方式,直接通过其计算后的结果来验证。
LN中是一个样本的所有特征来计算均值和方差,
如此段代码中,第一个样本的均值为:[(4*1) + (4*2) + (4*3)] / 12 = 2
Normaliztion的计算公式如下图
而此样本中的第二个维度的特征是全为2,所以经过normalize后,全为0(x = 2 ,均值 = 2,则分子=0)。
正如上展示的输出一样,经过LN后的第一个样本数据的第二个维度的特征全是0
以上验证了LN的计算方式
"""
4.Instance Normalization
- 起因:BN在图像生成中不适用,一个batch中图像样本有不同的模式,不同的风格。
- 思路:逐Instance(channel)的计算均值和方差
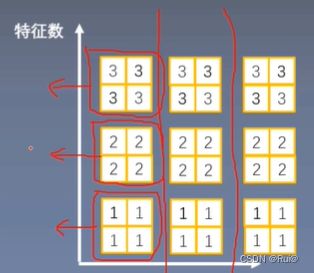
- 计算方式:对于一个batch的图像,对其每一个样本中的通道进行计算均值和方差的计算,并以此在每个通道上进行normalization
4.1.pytorch中Instance Normalization
nn.InstanceNorm
主要参数:
- num_features:一个样本特征数量(最重要,如上图就是3)
- eps:分母修正项
- momentum:指数加权平均估计当前mean/var
- affine:是否需要affine transform
- track_running_stats:是训练状态,还是测试状态
4.2 通过pytorch验证其计算方式
代码以及结果展示推导如下:
"""
模拟出一个batch的经过IN的数据集
"""
batch_size = 3
num_features = 3
momentum = 0.3
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0) # 4D
print("Instance Normalization")
print("input data:\n{} shape is {}".format(feature_maps_bs, feature_maps_bs.shape))
"""
模拟了一个batch,有3个样本,每个样本有3个通道(特征图),每个特征大小为(2,2)
具体值如下输出:
Instance Normalization
input data:
tensor([[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]],
[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]],
[[[1., 1.],
[1., 1.]],
[[2., 2.],
[2., 2.]],
[[3., 3.],
[3., 3.]]]]) shape is torch.Size([3, 3, 2, 2])
"""
"""
此处IN的创建第一个参数是输入有几个通道数(特征图)
"""
instance_n = nn.InstanceNorm2d(num_features=num_features, momentum=momentum)
for i in range(1):
outputs = instance_n(feature_maps_bs)
print(outputs)
"""
可以看到此处LN后的结果全为0
此处每个样本数据都一致,以第一个样本为例
每个通道上进行计算均值,第一个通道 (1+1+1+1) / 4 = 1,同理 第2和3通道的均值为2,3
经过normalization的公式(如下图)计算后都为0
以此验证了IN的计算方式
以下输出:
tensor([[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]],
[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]],
[[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]],
[[0., 0.],
[0., 0.]]]])
"""
5.Group Normalization
- 起因:小batch样本中,BN估计的值不准
- 思路:数据不够,通道来凑
- 注意事项:不再有running_mean和running_var,gamma和beta是逐通道的
- 计算方式:在一个样本的特征通道上(也就是特征数上)进行分组,然后每组进行均值和方差的计算
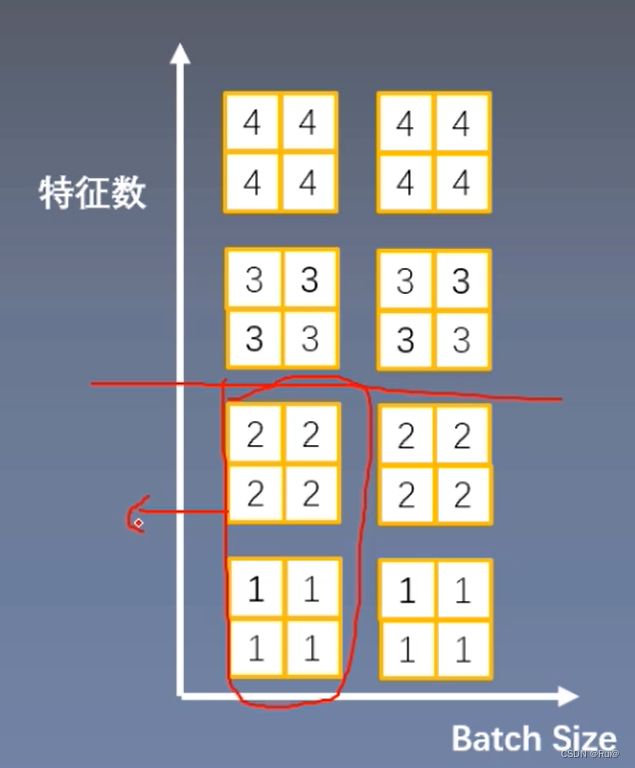
5.1.pytorch中groupNorm
nn.GroupNorm
主要参数:
- num_groups:分组数
- num_channels:通道数(特征数)
- eps:分母修正项
- affine:是否需要affine transform
5.2 通过pytorch验证其计算方式
代码以及结果展示推导如下:
"""
模拟一个batch大小的经过GN的数据集
"""
batch_size = 2
num_features = 4
num_groups = 2 # 3 Expected number of channels in input to be divisible by num_groups
features_shape = (2, 2)
feature_map = torch.ones(features_shape) # 2D
feature_maps = torch.stack([feature_map * 1 if i == 1 or i == 0 else feature_map * (i + 1) for i in range(num_features)], dim=0) # 3D
feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0) # 4D
"""
生成一个GN层,同时传参组数,和每个样本的特征图数(通道数)。注:此处必须整除
"""
gn = nn.GroupNorm(num_groups, num_features)
outputs = gn(feature_maps_bs)
print(feature_maps_bs.shape)
print(feature_maps_bs)
"""
模拟一个batch,有2个样本,每个样本4个通道(特征图),每个特征图大小(2,2)
以上输出如下:
torch.Size([2, 4, 2, 2])
下面是第一个样本的数据
tensor([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]],
[[3., 3.],
[3., 3.]],
[[4., 4.],
[4., 4.]]])
"""
print("Group Normalization")
print(gn.weight.shape)
print(outputs[0])
"""
以上输出:
torch.Size([4])
此权重大小为4,验证了可学习参数是逐通道数(特征图)的
tensor([[[ 0.0000, 0.0000],
[ 0.0000, 0.0000]],
[[ 0.0000, 0.0000],
[ 0.0000, 0.0000]],
[[-1.0000, -1.0000],
[-1.0000, -1.0000]],
[[ 1.0000, 1.0000],
[ 1.0000, 1.0000]]], grad_fn=)
GN创建时,组数为2,特征图数为4。则分为2组,一组2个特征图。
以第一个样本为例,分为2组,前2个通道为第一组
对第一组计算均值,(1+1+1+1+1+1+1+1) / 8 = 1
和LN IN同理,经过normalization计算后结果都为0
此处第一组的结果也0,以此验证了其计算方式
"""