传统机器学习介绍

传统机器学习

机器学习可以分为传统机器学习和深度学习。我先从传统机器学习的几个比较经典的方法出发，研究手写数据集的准确率。

1.1 K-近邻算法(KNN)介绍

K-近邻算法是一种惰性学习模型(lazy learning)，也称为基于实例学习模型，这与**勤奋学习模型(eager learning)**不一样。例如线性回归模型就是属于勤奋学习模型。

勤奋学习模型在训练模型的时候会很耗资源，它会根据训练数据生成一个模型，在预测阶段直接带入数据就可以生成预测的数据，所以在预测阶段几乎不消耗资源

惰性学习模型在训练模型的时候不会估计由模型生成的参数，他可以即刻预测，但是会消耗较多资源，例如KNN模型，要预测一个实例，需要求出与所有实例之间的距离。

K-近邻算法是一种非参数模型，参数模型使用固定的数量的参数或者系数去定义模型，非参数模型并不意味着不需要参数，而是参数的数量不确定，它可能会随着训练实例数量的增加而增加，当数据量大的时候，看不出解释变量和响应变量之间的关系的时候，使用非参数模型就会有很大的优势，而如果数据量少，可以观察到两者之间的关系的，使用相应的模型就会有很大的优势。

原理:存在一个样本集，也就是训练集，每一个数据都有标签，也就是我们知道样本中每个数据与所属分类的关系，输入没有标签的新数据后，新数据的每个特征会和样本集中的所有数据对应的特征进行比较，算出新数据与样本集其他数据的欧几里得距离，这里需要给出K值，这里会选择与新数据距离最近的K个数据，其中出现次数最多的分类就是新数据的分类，一般k不会大于20。

K近邻算法(knn)实现步骤：

• 计算当前点与已知类别数据集中的点的距离
• 距离递增排序，选出距离最小的k个点
• 确定前k个点类别出现的频率
• 将频率最高的类别作为当前点的预测分类

1.2 支持向量机(SVM）介绍

支持向量机（Support Vector Machine, SVM）是一类按监督学习（supervised learning）方式对数据进行二元分类（binary classification）的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane）。

SVM使用铰链损失函数（hinge loss）计算经验风险（empirical risk）并在求解系统中加入了正则化项以优化结构风险（structural risk），是一个具有稀疏性和稳健性的分类器。SVM可以通过核方法（kernel method）进行非线性分类，是常见的核学习（kernel learning）方法之一。

SVM在解决小样本、非线性及高维模式识别中表现出许多特有的优势，是迄今为止具有最小化分类错误率和最大化泛化能力的一种强有力的分类工具，已经在模式识别、回归分析等机器学习领域得到广泛应用，成为机器学习领域研究的热点。

SVM是一种最小化结构风险的机器学习算法，克服了经验风险最小化机器学习算法所带来的分类函数推广能力差，即分类器泛化能力差的缺憾。SVM 建立在统计学习理论的VC维和结构风险最小化原理基础上，能根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，获得最好的推广能力也即泛化能力。

对于线性可分的两类样本，SVM算法可以学习得到一个将这两类样本分开的最优分类超平面f(x)=+b=0。该最优分类超平面只需要少数几个样本就可以确定，这几个样本构成支持向量。该最优分类超平面是具有最大几何间隔的超平面，即样本集到该最优分类超平面的欧氏距离最大，就是样本集中距离超平面最近的样本到超平面的欧氏距离达到最大，因此这个最优分类超平面一定在两类中间，使得两类样本集到超平面的距离相等。此时，样本被误分的次数≤(2R/γ)2，γ是几何间隔，R是样本的最长向量长度值，R代表了样本的分布广度。因此，最大化几何间隔作为SVM 学习的目标，就是最小化样本错分率。

对于线性不可分的两类样本，SVM通过核函数将低维输入空间线性不可分的样本映射到高维特征空间成为线性可分的样本，在高维特征空间求解线性可分的两类样本的最优分类超平面。

常用的核函数有：线性核函数K(x,x)=x·x，多项式核函数函数K(x,x)=(x·x+1)d，径向基核函数，S型核函数等。其中径向基核函数几乎可以解决所有的分类问题。但是在具有高维特征的问题中，比如基因选择、文本分类等，线性核函数经常被使用。

对于带有噪音的近似可分两类样本，SVM通过引入松弛变量得到一阶或二阶的软间隔分类器，并通过惩罚因子调控噪音点对最优分类超平面的影响，惩罚因子越大噪音点的影响越强。

1.3 朴素贝叶斯法介绍

朴素贝叶斯

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。简单来说，朴素贝叶斯分类器假设样本每个特征与其他特征都不相关。举个例子，如果一种水果具有红，圆，直径大概4英寸等特征，该水果可以被判定为是苹果。尽管这些特征相互依赖或者有些特征由其他特征决定，然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。尽管是带着这些朴素思想和过于简单化的假设，但朴素贝叶斯分类器在很多复杂的现实情形中仍能够取得相当好的效果。朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数（离散型变量是先验概率和类条件概率，连续型变量是变量的均值和方差）。

1.3.1 贝叶斯分类模型

$$P(Y|X）=\frac{P(Y）P(X|Y）}{P(X）}$$
其中，X表示属性集，Y表示类变量，P(Y)为先验概率，P(X|Y)为类条件概率，P(X)为证据，P(Y|X)为后验概率。贝叶斯分类模型就是用先验概率P(Y)、类条件概率P(X|Y)和证据P(X)来表示后验概率。在比较Y的后验概率时，分母中的证据P(X)总是常数，因此可以忽略不计。先验概率P(Y)可以通过计算训练集中属于每个类的训练记录所占的比例很容易估计。对类条件概率P(X|Y)的估计，不同的实现决定不同的贝叶斯分类方法，常见的有朴素贝叶斯分类法和贝叶斯信念网络。

1.3.2 朴素贝叶斯分类模型

朴素贝叶斯分类法在估计类条件概率P(X|Y)时假设属性之间条件独立，条件独立假设可以表示如下：
$$P(X|Y=y）=\prod _{i=1}^{d}P(X_i|Y=y）$$
其中，d为每条记录的属性个数

朴素贝叶斯分类法模型如下：
$$P(Y=y_j|X）=\frac{P(Y=y_j){\prod }_{i=1}^{d}P(X_i|Y=y_j)}{P(X)}$$
模型中，对于所有的Y,P（X）是固定的，所以上述模型等价于：
$$P(Y=y_j|X）=argma{x}_{y_j}P(Y=y_j)\prod _{i=1}^{d}P(X_i|Y=y_j)$$
当属性是离散型时，类的先验概率可以通过训练集的各类样本出现的次数来估计，例如：A类先验概率=A类样本的数量/样本总数。类条件概率$ P(X_i = x_i|Y_j = y_j）$可以根据类$y_j$中属性值等于$x_i$的训练实例的比例来估计。\ast \ast 当属性是连续型时\ast \ast ，有两种方法来估计属性的类条件概率。第一种方法是把每一个连续的属性离散化，然后用相应的离散区间替换连续属性值，但这种方法不好控制离散区间划分的粒度。如果粒度太细，就会因为每一个区间中训练记录太少而不能对$P(X|Y)$做出可靠的估计，如果粒度太粗，那么有些区间就会含有来自不同类的记录，因此失去了正确的决策边界。第二种方法是，可以假设连续变量服从某种概率分布，然后使用训练数据估计分布的参数，高斯分布通常被用来表示连续属性的类条件概率分布。

高斯分布有两个参数，均值$u$和方差${\sigma }^2$,对于每个类$y_i$,属性$X_i$的类条件概率等于：
$$P(X_i=x_i|Y=y_j）=\frac{1}{\sqrt{2\pi }{{\sigma }_{ij}}^2}{e}^{-\frac{{(x_i-u_{ij})}^2}{2{\sigma }_{ij}^2}}$$
参数$u_{ij}$可以用类$y_j$的所有训练记录关于$X_i$的样本值来估计，同理，${\sigma }_{ij}^2$可以用这些训练记录的样本方差来估计

1.4 决策树介绍

决策树(Decision Tree）是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干，故称决策树。

决策树是一种树形结构，其中每个内部节点表示一个属性上的测试，每个分支代表一个测试输出，每个叶节点代表一种类别。

机器学习中，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术，可以用于分析数据，同样也可以用来作预测。

决策树实际上是一个if-then规则的集合。例如，现在要做一个决策：周末是否要打球，我们可能要考虑下面几个因素。第一，天气因素，如果是晴天，我们就打球，如果是雨天我们就不打球。第二，球场是否满员，如果满员，我们就不打球，如果不满员我们就打球。第三，是否需要加班，如果加班则不打球，如果不需要加班则打球。这样我们就形成了一个决策树，如图 1 所示。

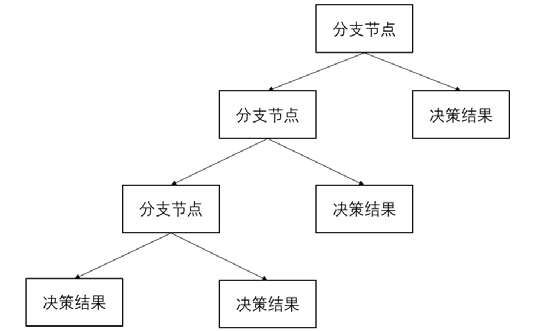
可以将这个决策过程抽象一下，每个决策点称为分支节点，如图 2 所示。

1.5 AdaBoost介绍

AdaBoost

AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写，是一种机器学习方法，由Yoav Freund和Robert Schapire提出。AdaBoost方法的自适应在于：前一个分类器分错的样本会被用来训练下一个分类器。AdaBoost方法对于噪声数据和异常数据很敏感。但在一些问题中，AdaBoost方法相对于大多数其它学习算法而言，不会很容易出现过拟合现象。AdaBoost方法中使用的分类器可能很弱（比如出现很大错误率），但只要它的分类效果比随机好一点（比如两类问题分类错误率略小于0.5），就能够改善最终得到的模型。而错误率高于随机分类器的弱分类器也是有用的，因为在最终得到的多个分类器的线性组合中，可以给它们赋予负系数，同样也能提升分类效果。

AdaBoost方法是一种迭代算法，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率。每一个训练样本都被赋予一个权重，表明它被某个分类器选入训练集的概率。如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它被选中的概率就被降低；相反，如果某个样本点没有被准确地分类，那么它的权重就得到提高。通过这样的方式，AdaBoost方法能“聚焦于”那些较难分（更富信息）的样本上。在具体实现上，最初令每个样本的权重都相等，对于第k次迭代操作，我们就根据这些权重来选取样本点，进而训练分类器Ck。然后就根据这个分类器，来提高被它分错的的样本的权重，并降低被正确分类的样本权重。然后，权重更新过的样本集被用于训练下一个分类器Ck。整个训练过程如此迭代地进行下去。

• 预设条件
  假设我们的训练集样本是： $X=(x_1,y_1)，(x_2,y_2)，...，(x_m,y_m)$
  训练集的在第k个弱学习器的样本权重系数为：$$D(k)=(w_{k1},w_{k2},...,w_{km});\sum _{i=1}^m{w}_{ki}=1;w_{1i}=\frac{1}{m};i=1,2,..,m$$

• 分类误差率
  分类问题的误差率很好理解和计算。由于多元分类是二元分类的推广，这里假设我们是二元分类问题，输出为{-1，1}，则第k个弱分类器$G_k(x)$在训练集上的分类误差率为：
  $$e_k=P(G_k(x_i)\ne y_i)=\sum _{i=1}^m{w}_{ki}I(G_k(x_i)\ne y_i)$$

• 样本权重
  如何更新样本权重D。假设第k个弱分类器的样本集权重系数为 $D(k)=(w_{k1},w_{k2},...,w_{km})$ ，则对应的第k+1个弱分类器的样本权重系数为：
  $$w_{k+1,i}=\frac{w_{ki}}{Z_K}exp(-{\alpha }_k{y}_i{G}_k(x_i))$$
  这里$Z_k$是规范化因子：
  $$Z_k=\sum _{i=1}^m{w}_{ki}exp(-{\alpha }_k{y}_i{G}_k(x_i))$$
  从$w_{k+1,i}$计算公式可以看出，如果第i个样本分类错误，则 $y_i{G}_k(x_i)<0$ ，导致样本的权重在第k+1个弱分类器中增大，如果分类正确，则权重在第k+1个弱分类器中减少.不改变所给的训练集数据，通过不断的改变训练样本的权重，使得训练集数据在弱分类器的学习中起不同的作用。

• 弱学习器的权重系数
  接着我们看弱学习器权重系数,对于二元分类问题，第k个弱分类器$G_k(x)$的权重系数为：
  $${\alpha }_k=\frac{1}{2}log\frac{1-e_k}{e_k}$$
  （注意这个权重系数的定义，指数损失的由来）

为什么这样计算弱学习器权重系数？从上式可以看出，如果分类误差率$e_k$越大，则对应的弱分类器权重系数${\alpha }_k$越小。也就是说，误差率小的弱分类器权重系数越大。

• 结合策略
  Adaboost分类采用的是加权平均法，最终的强分类器为：
  $$f(x)=sign(\sum _{k=1}^K{\alpha }_k{G}_k(x))$$
  系数${\alpha }_k$表示了弱分类器$G_k(x)$的重要性，这里所有$\alpha$之和并不为1，$f(x)$的符号决定实例$x$的类，$f(x)$的绝对值表示分类的置信度。

1.6 python实现

传统机器学习

# 1.导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.datasets import load_digits
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import MultinomialNB
from sklearn.ensemble import AdaBoostClassifier

from sklearn.metrics import accuracy_score

# 2.加载数据并探索

# 加载数据
digits = load_digits()
data = digits.data

# 数据探索
print(data.shape)
# 查看第一幅图像
print(digits.images[0])
# 第一幅图像代表的数字含义
print(digits.target[0])

# 将第一幅图像显示出来
plt.imshow(digits.images[0])
plt.show()

# 3.分割数据集并规范化

# 数据及目标
data1 = digits.data
target1 = digits.target

# # 数据增广
# data2 = np.vstack((data1, data1))
# target2 = np.hstack((target1, target1))
data2 = np.vstack((data1, data1, data1))
target2 = np.hstack((target1, target1, target1))
# 分割数据，将25%的数据作为测试集，其余作为训练集（你也可以指定其他比例的数据作为训练集）
# train_x, test_x, train_y, test_y = train_test_split(data1, target1, test_size=0.25)
train_x, test_x, train_y, test_y = train_test_split(data2, target2, test_size=0.25)

# 采用z-score规范化
ss = StandardScaler()
train_ss_scaled = ss.fit_transform(train_x)
test_ss_scaled = ss.transform(test_x)
# 采用0-1归一化，有分类器不能为负数，如多项式朴素贝叶斯分类
mm = MinMaxScaler()
train_mm_scaled = mm.fit_transform(train_x)
test_mm_scaled = mm.transform(test_x)
# 4.建立模型，并进行比较
models = {}
models['knn'] = KNeighborsClassifier()
models['svm'] = SVC()
models['bayes'] = MultinomialNB()
models['tree'] = DecisionTreeClassifier()
models['ada'] = AdaBoostClassifier(base_estimator=models['tree'], learning_rate=0.1)

for model_key in models.keys():
    if model_key == 'knn' or model_key == 'svm' or model_key == 'ada':
        model = models[model_key]
        model.fit(train_ss_scaled, train_y)
        predict = model.predict(test_ss_scaled)
        print(model_key, "准确率：", accuracy_score(test_y, predict))
    else:
        model = models[model_key]
        model.fit(train_mm_scaled, train_y)
        predict = model.predict(test_mm_scaled)
        print(model_key, "准确率: ", accuracy_score(test_y, predict))

分析以上结果，可以看到，除朴素贝叶斯模型的准确率只有0.90，KNN的准确率只有0.97，预测效果不是特别好以外，其他模型的准确率都已经高达0.993以上了