AICS188-Project6-Q1-Q3
一、问题描述
1.总述
本项目的任务是实现价值迭代和 Q-learning。首先在 Gridworld(值迭代)上测试智能体,然后将它们应用到模拟机器人控制器 (Crawler) 和 Pacman。
2.Q1:值迭代
本题要求在valueIterationAgents.py 的ValueIterationAgent 中实现一个值迭代的智能体,它是一个离线规划器而非强化学习智能体,因此相关的训练选项是它在初始规划阶段应该运行的值迭代的迭代次数(-i)。 ValueIterationAgent 在构造时采用 MDP 并在构造函数返回之前运行指定迭代次数的值迭代。值迭代计算最优值的 k 步估计Vk,除了 runValueIteration 之外,还要实现以下方法为 ValueIterationAgent 使用Vk:
computeActionFromValues(state):根据 self.values 给出的值函数计算最佳行动;
computeQValueFromValues(state, action) :返回由 self.values 给出的值函数给出的 (state, action) 对的 Q 值。
注意:
1.值是平方数,Q 值是四分之一平方数,策略是每个方块中的箭头。
2.用值迭代的“批处理”版本,其中每个向量Vk 从固定向量Vk-1计算的而不是一个单独的权重向量就地更新的“在线”版本。这意味着当一个状态的值在迭代k中更新时基于其后继状态的值,值更新计算中使用的后继状态值应该是来自迭代k-1中的值,即使某些后继状态已经在迭代k中更新 。
3.从深度k的值合成的策略实际上反映了k+1的奖励,同样,Q 值也将反映比值多一个奖励。
3.Q2: 政策
DiscountGrid的布局如下,该网格有两个具有正收益的终端状态(在中间行),一个收益为 +1 的关闭退出和收益为 +10 的远程退出。网格的底行由具有负收益的终端状态组成(以红色显示);这个“悬崖”区域中的每个州的收益为 -10。起始状态是黄色方块。我们区分两种类型的路径:(1)“冒险悬崖”并在网格底行附近行进的路径;这些路径较短,但有可能获得较大的负收益,并由下图中的红色箭头表示。(2)“避开悬崖”并沿着网格的顶部边缘行进的路径。这些路径更长,但不太可能产生巨大的负收益。这些路径由下图中的绿色箭头表示。

在这个问题中,我们将为此 MDP 选择折扣、噪声和生活奖励参数的设置,以生成几种不同类型的最佳策略。为每个部分设置的参数值应该具有以下属性:如果智能体在 MDP 中遵循其最佳策略,它将表现出给定的行为。如果参数的任何设置都没有实现特定行为,则通过返回 string 断言该策略是不可能的’NOT POSSIBLE’。
以下是您应该尝试生成的最佳策略类型:
1.更喜欢关闭退出(+1),冒着悬崖的风险(-10)
2.更喜欢关闭出口(+1),但要避开悬崖(-10)
3.偏爱远处出口(+10),冒着悬崖(-10)
4.喜欢远处的出口(+10),避开悬崖(-10)
5.避免出口和悬崖(因此一集永远不应该终止)
4.Q3:Q-Learning
前面值迭代代理实际上并未从经验中学习。相反,它会在与真实环境交互之前考虑其 MDP 模型以得出完整的策略。当它确实与环境交互时,它只是遵循预先计算好的策略(例如,它成为一个反射代理)。这种区别在像 Gridword 这样的模拟环境中可能很微妙,但在真实 MDP 不可用的现实世界中非常重要。所以本题要编写一个 Q-learning 智能体,它在构造方面做的很少,而是通过它的update(state, action, nextState, reward)方法从与环境的交互中反复试验来学习。本题必须实现computeValueFromQValues,computeActionFromQValues,update,getQValue方法。对于computeActionFromQValues,应该随机打破关系以获得更好的行为。该random.choice()功能会有所帮助。在一个特定的状态,动作,智能体还没有见过还有Q值,特别是零Q值,如果一切,智能体的行动已经见过有一个负的Q值,一个看不见的行动可能是最佳的。
注意:确保在computeValueFromQValues和computeActionFromQValues函数中,只能通过调用来访问 Q 值getQValue。重写getQValue以使用状态-动作对的特征而不是直接使用状态-动作对。
二、知识储备
1.强化学习:
强化学习可以看做是“摸黑探索”,在第一次从Start出发的时候,智能体完全不知道如何才能到达“奖励”的位置,可能一脚就踏入了惩罚。但经过一次又一次的尝试走向终点,他就会发现有些路会通向惩罚,不能走,并逐渐找到Reward最大的路径。
2.值迭代:
什么是值迭代(Gridworld):如下图,智能体在蓝点位置,灰色的格子表示不能走的障碍,右上角的+1,-1表示的是格子世界的终点,我们只要走到这里就算完成了目标,+1的部分表示的是“奖励”,而-1的部分表示的是“惩罚”。

与值迭代有关的概念:
State:状态,即智能体在Grid World的哪个格子;
Action:行为,即智能体会朝上下左右(东南西北)的格子移动;
Reward:奖励值(不同于终点的+1那个奖励),即智能体在当前State下能得到的奖励;
GAMMA:奖励折扣。越远的节点影响越小。
注意:由于是马尔科夫模型,因此是越靠近当前节点的值对其影响越大,越远的影响越小。
3.马尔可夫决策过程(MDP):
马尔科夫决策过程(Markov Decision Process,MDP):它提供了一套为在结果部分随机、部分在决策者的控制下的决策过程建模的数学框架。
MDP形式化地描述了一种强化学习环境,它的特点是环境完全可观测,即马尔科夫性质(当前状态可以完全表征过程,即根据当前状态,即可推演接下来的状态)
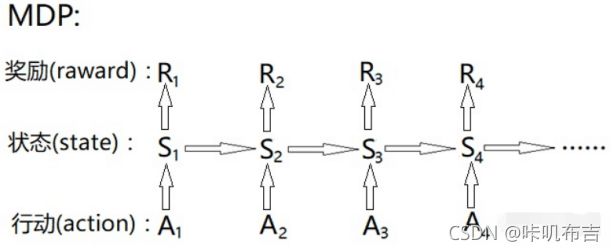
过程:
(1)从状态s0开始;
(2)智能体选择某个动作a0∈A;
(3)智能体得到奖励R(s0,a0);
(4)MDP随机转移到下一个状态s1~Ps0a0,即s0通过Ps0a0的状态概率分布,转移到下一个状态s1;
寻找最优化策略的两种方法:值迭代和策略迭代,对应一二问。
三、解答过程
1.Q1:值迭代
值迭代伊始只能得到起点和终点的值,对其他信息一无所知;
二次迭代分三步:1.得到所有action列表; 2.计算每个action可能获得的奖励之和;3.计算当前格子的最优方向选择。
步骤:
1.遍历每一个state(格子)
2.遍历当前state的每一个合法action(上下左右)
3.对执行action移动到的所有state’的reward进行求和
4.保存能获得最大reward的action,并将reward值记录在格子(state)上
代码如下:
def runValueIteration(self):
# Write value iteration code here
#Q1:值迭代
for i in range(self.iterations):
new_counter = util.Counter()
for state in self.mdp.getStates():
if not self.mdp.isTerminal(state):
best_q = float(’-inf’)
#找到最优选择即奖励值大的一个
for action in self.mdp.getPossibleActions(state):
curr_q = self.computeQValueFromValues(state, action)
best_q = max(best_q, curr_q)
new_counter[state] = best_q
self.values = new_counter
#计算最佳行动
def computeQValueFromValues(self, state, action):
“”"
Compute the Q-value of action in state from the
value function stored in self.values.
“”"
#初值为0
q = 0
for next, t_prob in self.mdp.getTransitionStatesAndProbs(state, action):
#按照提示来的计算公式
q += t_prob * (self.mdp.getReward(state, action, next) + (self.discount * self.values[next]))
return q
#返回 (state, action) 对应的 Q 值
def computeActionFromValues(self, state):
“”"
The policy is the best action in the given state
according to the values currently stored in self.values.
You may break ties any way you see fit. Note that if
there are no legal actions, which is the case at the
terminal state, you should return None.
“”"
best_action = None
best_q = float(’-inf’)
for action in self.mdp.getPossibleActions(state):
curr_q = self.computeQValueFromValues(state, action)
best_q = max(best_q, curr_q)
if best_q == curr_q:
best_action = action
return best_action
2.Q2:政策
按照它的提示即可:
1.更喜欢关闭退出(+1),冒着悬崖的风险(-10)
def question2a():
answerDiscount = 0.1
answerNoise = 0
answerLivingReward = -0.1
return answerDiscount, answerNoise, answerLivingReward
# If not possible, return ‘NOT POSSIBLE’
2.更喜欢关闭出口(+1),但要避开悬崖(-10)
def question2b():
answerDiscount = 0.1
answerNoise = 0.1
answerLivingReward = -0.1
return answerDiscount, answerNoise, answerLivingReward
# If not possible, return ‘NOT POSSIBLE’
结果分析:
3.偏爱远处出口(+10),冒着悬崖(-10)
def question2c():
answerDiscount = 0.9
answerNoise = 0
answerLivingReward = -0.1
return answerDiscount, answerNoise, answerLivingReward
# If not possible, return ‘NOT POSSIBLE’
4.喜欢远处的出口(+10),避开悬崖(-10)
def question2d():
answerDiscount = 0.9
answerNoise = 0.1
answerLivingReward = -0.1
return answerDiscount, answerNoise, answerLivingReward
# If not possible, return ‘NOT POSSIBLE’
5.避免出口和悬崖(因此一集永远不应该终止)
def question2e():
answerDiscount = 0
answerNoise = 1
answerLivingReward = 1
return answerDiscount, answerNoise, answerLivingReward
# If not possible, return ‘NOT POSSIBLE’
3.Q3:Q-Learning
QLearning是强化学习算法中value-based的算法,Q即为Q(s,a)就是在某一时刻的 s 状态下(s∈S),采取 动作a (a∈A)动作能够获得收益的期望,环境会根据agent的动作反馈相应的回报reward r,所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作。
计算公式:
![]()
def init(self, **args):
“You can initialize Q-values here…”
#初始化Q
ReinforcementAgent.init(self, **args)
self.q = util.Counter()
def getQValue(self, state, action):
“”"
Returns Q(state,action)
Should return 0.0 if we have never seen a state
or the Q node value otherwise
“”"
# 将参数指定的Q值返回
return self.q[(state, action)]
#根据 self.values 给出的值函数计算最佳行动
def computeValueFromQValues(self, state):
“”"
Returns max_action Q(state,action)
where the max is over legal actions. Note that if
there are no legal actions, which is the case at the
terminal state, you should return a value of 0.0.
“”"
max_q = float(’-inf’)
# 获取所有可行的action
for action in self.getLegalActions(state):
curr_q = self.getQValue(state, action)
max_q = max(max_q, curr_q)
#max_q没有更新,则返回0,否则返回max_q
if max_q == float(’-inf’):
return 0.0
else:
return max_q
#返回由 self.values 给出的值函数给出的 (state, action) 对的 Q 值
def computeActionFromQValues(self, state):
“”"
Compute the best action to take in a state. Note that if there
are no legal actions, which is the case at the terminal state,
you should return None.
“”"
best_action = None
best_q = float(’-inf’)
for action in self.getLegalActions(state):
curr_q = self.getQValue(state, action)
best_q = max(best_q, curr_q)
if best_q == curr_q:
best_action = action
return best_action
def getAction(self, state):
“”"
Compute the action to take in the current state. With
probability self.epsilon, we should take a random action and
take the best policy action otherwise. Note that if there are
no legal actions, which is the case at the terminal state, you
should choose None as the action.
HINT: You might want to use util.flipCoin(prob)
HINT: To pick randomly from a list, use random.choice(list)
“”"
# Pick Action
legalActions = self.getLegalActions(state)
action = None
“*** YOUR CODE HERE ***”
util.raiseNotDefined()
return action
def update(self, state, action, nextState, reward):
“”"
The parent class calls this to observe a
state = action => nextState and reward transition.
You should do your Q-Value update here
NOTE: You should never call this function,
it will be called on your behalf
“”"
curr_q = self.getQValue(state, action)
rhs = (self.discount * self.getValue(nextState)) + reward
self.q[(state, action)] = (1-self.alpha) * curr_q + self.alpha * rhs
结果如下:
四、思考感悟
- 为什么智能体的行为不总是按照计划走的,当发出向上走的指令时,他只有80%的可能会正确执行向左或者向右走的概率各占10%。同样,发出向右走的指令时,也会各有10%的几率向上或者向下走?
因为如果智能体严格按照规定来的话,那就是普通的搜索问题,可以用DFS或者BFS求解;但这样就有弊端:1、前提得知道全部信息;2、假如出口无法用单纯的搜索发现,只有在智能体移动到出口那个位置,才知道这里是出口,就无法解决。所以当我们掌握的信息很少的时候,做出抉择就只能依靠概率。这也就是值迭代的的目的,即通过不断的学习,最终迭代出在当前状态下,执行哪个行动能更高概率的获得奖励。
2.值迭代与Q-Learning?
值迭代靠概率工作,依照固定公式计算,有弊端:
1.现实世界中,你不可能获得所有的状态;
2.现实世界中,到下一个状态的概率不可能是一个固定值;
3.现实世界中,行动也不是固定值。
Q-Learning:Q Learning采用的是一种不断试错方式学习,针对不能得到所有状态和概率不固定的问题,Q Learning使用了下面的解决办法:
1.计算的时候不会遍历所有的格子,只管当前状态,当前格子的reward值
2.不会计算所有action的reward,每次行动时,只选取一个action,只计算这一个action的reward值迭代在计算reward的时候,会得到每个action的reward,并保留最大的。而Q Learning在计算reward的时候,虽然也会每个action的reward,但会全部都保留下来。
3.运行时遇到一个错误:错误和解决方法参考了如下链接:
https://www.jianshu.com/p/c8f265174570
