数字图像直方图匹配或规定化Histogram Matching (Specification)处理
☞ ░ 前往老猿Python博文目录 https://blog.csdn.net/LaoYuanPython ░
一、引言
在《数字图像处理:直方图均衡(Histogram Equalization)的原理及处理介绍》了直方图均衡,直方图均衡能自动地确定均衡需要的变换函数,该函数能产生有灰度值均匀直方图的输出图像。当需要对一副图像自动增强时,这是一种好方法,因为这种处理结果可以预知(predictable)、实现简单。但是对某些应用,基于统一的直方图的基础增强(base enhancement)并不是最好的方法,特别地有时处理人员希望能指定结果图像的直方图形状(specify the shape of the histogram),这时就需要用到直方图匹配(规定化)。
本文是《数字图像处理》第三章直方图处理中的直方图匹配或规定化相关章节的内容,阅读本文需要具备导数和微积分相关知识。如果需要复习或学习相关高数知识,请参考《人工智能数学基础》。
二、知识概要:直方图匹配或规定化
2.1、概述
直方图匹配(Histogram Matching ),又称为直方图规定化(Histogram Specification),是指在处理图像时,由处理人员指定输出图像的直方图形状。
老猿注:
- 指定直方图形状应该是通过指定直方图的PDF函数来实现的;
- 本部分的原理没有采用原文相同的方式介绍,因为原文比较拗口,乍一看有点难以理解,老猿按自己的理解来介绍。
2.2、连续灰度值的非数字图像直方图匹配或规定化
2.2.1、相关原理
在《数字图像处理:直方图均衡(Histogram Equalization)的原理及处理介绍》介绍了对于非数字图像的灰度值连续图像,对于灰度值为r的图像到直方图均衡后灰度为s的图像有如下公式:

现假设针对该输入图像,存在另一个灰度值集合z的图像,其图像内容与灰度值集合为r的图像是同一副图像,只是灰度值不同(这里的r、z、s在公式内是表示单个像素的灰度值,适用于图像的每个像素,同时在描述时r、z、s又表示了同一个图像所有像素的灰度集合的阵列)。
类似式(3.3-10),z对应的灰度图像通过如下函数G(z)可以转换为s对应的图像:
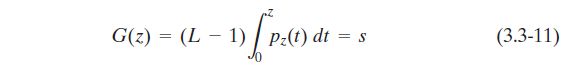
即可得:
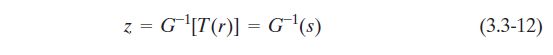
这是因为针对同一图像有不同灰度分布的情况,都可以通过直方图均衡化为灰度值均衡的图像,这就意味着两副不同灰度值的同样内容的图像都可以通过直方图均衡后的结果图像关联起来,并以此为中介求得两副相同内容但灰度值不同的图像之间的灰度的映射关系。
由式(3.3-12) z = G-1|T(r)|可知:z和r的映射只需要z和r对应的两副图像的灰度值的概率密度函数经过定积分以及四则运算就可以求出。
这就是说,两副内容相同灰度值不同的图像,可以很方便地找到两副图像的灰度映射关系。这也就是为什么该灰度变换被称为直方图匹配或直方图规定化的原因,它们的目的就是给定两副相同内容不同灰度分布图像,通过这两副图像本身的灰度概率密度函数就可以找到二者的映射关系。
2.2.2、连续灰度图像的直方图规定化处理步骤
通过以上三个式子可知,使用下列步骤,可由一幅给定图像得到一幅其灰度级具有指定概率密度函数的图像:
- 首先由输入图像的概率密度函数PDF使用式(3.3-10)对输入图像进行均衡得到像素值为s的输出图像;
- 使用式(3.3-11)结合输出图像的PDF求得输出图像到直方图均衡像素值为s的图像的映射函数G(z);
- 对均衡后的图像像素值s进行G(z)的反变换G-1(s),就可以得到输出图像的像素值。
当所有像素都转换后,就可以得到PDF等于指定函数的输出图像。
2.2.3、连续灰度图像的直方图规定化案例
例:假设采用连续灰度值的一幅图像的灰度 PDF 为pr(r)= 2r/(L-1)²,0≤r≤(L-1),对于其他r值有pr(r)=0。寻找一个变换函数,使得产生的图像的灰度PDF是pz(z)=3z²/(L-1)³,0≤z≤(L-1),而对于其他z值有pz(z)=0。
注:上面pr、pz的字母r和z都是下标,表示不同的概率密度函数,为了输入方便就写成了pr、pz,下同。
解:
首先,我们对区间[0,L-1]寻找直方图均衡变换:
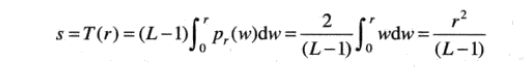
由定义可知,对于范围[0,L-1]外的值,该变换为0。按直方图均衡变换的处理可知,输人灰度值的平方除以(L-1)(老猿注:原文和译本这里都说是(L-1)²,经笔者仔细核实应该没有平方)将产生一幅灰度为s并具有均匀PDF的图像。
为了得到pz(z)=3z²/(L-1)³指定直方图的输出图像,在[0,L-1]区间上,pz(z)对应的直方图均衡变换公式为:

由定义可知在该区间外这个函数也为0。最后,我们要求G(z)=s. 但G(z)=z³/(L-1)²;因此z³/(L-1)²=s,可得:

这表明如果我们用(L-1)²乘以直方图均衡过的每一个像素,取该乘积的 1/3 次幂,结果将是一幅我们所期望的图像,该图像在区间[0,L-1]内z的灰度的PDF为pz(z)=3z²/(L-1)³。
因为s=r²/(L-1),我们可以直接由输入图像的灰度r生成z:

这样原图像中每一个像素值的平方与(L-1)相乘,然后再取该乘积的1/3次幕,将得到其灰度级z具有规定 PDF 的图像。
2.2.4 、连续灰度图像的直方图规定化小结
通过前面的原理及案例介绍,我们看到,连续灰度值的非数字图像的直方图规定化是很容易理解的,并且均衡输人图像的中间一步可以跳过;我们需要的是得到将r映射为s的变换函数T(r)。然后,这两步可以合并为从r到z的一步变换。即由:
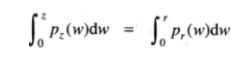
就可以求出T(r)。
但实际中,比较困难的是寻找T(r)和G的反函数形式,老猿认为由于输出图像的PDF是指定的,要找T(r)和G的反函数其实最困难的是一副输入图像的pr(r)怎么求得,因为输入图像只有各个图像元素的灰度值。
2.3、数字图像的直方图匹配或规定化
2.3.1、相关原理
连续灰度非数字图像求其映射到结果图像的映射函数比较困难(老猿认为主要是输入图像的PDF函数不好求),但幸运的是,计算机处理的是数字图像,因此相关解决方案可以大大简化。
在《数字图像处理:直方图均衡(Histogram Equalization)的原理及处理介绍》中介绍了数字图像直方图均衡变换的公式:

它是式(3.3-10)的离散形式,其中MN是图像像素的行数M与列数N的乘积,L为该表示图像灰度所在数字区间的上限,即图像中可能的灰度级数(intensity levels),如8bit图像为256,nj表示灰度值=j的像素个数,sk为输入图像灰度值为rk经过变换后映射到目标图像的灰度值,T(rk)表示将输入灰度值rk映射到sk的变换函数。
假设有一幅与输入图像内容相同灰度值不同的数字图像,假设其所有灰度值为Z0–Zq,每个灰度值zi出现的概率为pz(zi),那么对其进行直方图均衡对应的公式为式(3.3-11)对应的离散形式:

由于G(Zq)=Sk,因此有:
![]()
也就是说,对于灰度值为Sk的输入图像,对任意给定了输出图像的灰度值Zq,能找到一个从输入图像的灰度值映射到输出图像灰度值的变换函数,从而实现将输入图像映射到指定灰度值的输出图像。注意这里的Sk对应的灰度值为输入图像灰度为rk的灰度经直方图均衡变换后的灰度值。
实践中使用该方法处理数字图像时,由于数字图像灰度值的有限性,我们可以通过式(3.3-14)计算出指定灰度值的输出图像的直方图均衡后的近似灰度值(因为数字图像灰度值为整数,因此对式(3.3-14)的计算结果要进行四舍五入),从而我们就构建了一个Zq到Sk的映射表,这样无需求出G函数的反函数,直接通过映射表的Sk的取值查到Zq的取值。例如表中第64行记录的Sk值最接近给定的Sk值,则Zq的q值=63(注意是从0开始计数),故Z63是G(Zq)=Sk最近似解。
注意:使用式(3.3-14)计算出来的映射表,其数据源值为Z0-Zn,即对应灰度值范围为[0,L-1]的所有升序排列的整数,即Z0=0、Z1=1、…、n=l-1,其结果值为Sk对应的值。由于直方图均衡变换四舍五入取整后有可能Sk值组成的集合不包含[0,L-1]内所有整数。
2.3.2、数字图像直方图规定化处理步骤
假设Sk是直方图均衡后图像的灰度值,可以总结直方图规定化过程如下:
- 计算给定图像的直方图pr(r),并用它寻找式(3.3-13)的直方图均衡变换,把变换后图像的灰度sk四舍五入为范围[0,L-1]内的整数;
- 用式(3.3-14)对q=0、1、2、…、L-1计算变换函数G的所有值,其中pz(zi)是规定的直方图的值。把G的值四舍五入为范围[0,L-1]内的整数,并将G的输入和结果值存储在一个表中。注意式(3.3-14)是对规定的直方图进行直方图均衡变换,其结果为均衡化后直方图的灰度值,其值与步骤1中的sk一致,而输入是zi,zi的灰度值为i;
- 对每一个值sk,k=0、1、2、…、L-1,使用步骤2存储的G值寻找相应的zq值,以使G(zq)最接近sk,并存储这些从s到z的映射。当满足给定sk的zq值多于一个时(即映射不唯一时),按惯例选择最小的值;
- 首先对输入图像进行均衡,然后使用步骤 3 找到的映射把该图像中的每个均衡后的像素值sk映射为直方图规定化后的图像中的相应zq值,形成直方图规定化后的图像。正如连续情况那样,均衡输入图像的中间步骤是概念上的。它可以用合并两个变换函数T和G的反函数跳过这一步。
如早些时候提到的那样,对于满足条件(a’)严格单调和(b)函数值属于[0,L-1]范围的G的反函数,G必须是严格单调的,根据式(3.3-14),它意味着规定直方图的任何pz(zi)值都不能为零。当工作在离散数值的情况时,该条件可能不满足的事实并不是一个严重的实现问题,采用步骤3中取最小值的方式就可以解决。
注意:步骤4前面几句的翻译有问题,看起来莫名其妙,其对应英文原文如下:
Form the histogram-specified image by first histogram-equalizing the input image and then mapping every equalized pixel value, sk,of this image to the corresponding value zq in the histogram-specified image using the mappings found in step 3.
老猿将其翻译在付费文章《数字图像处理:直方图匹配或规定化Histogram Matching (Specification)原理及感悟》中进行了修改。上述处理步骤实际上还是不怎么好理解,老猿也在该文中按自己的理解进行了介绍。
2.3.3、数字图像的直方图规定化案例
假设一幅大小为64x64像素(MN=4096)的3比特图像(L=8)的灰度分布如表3.1所示,其中灰度级是范围[0,L-1]=[0,7]中的整数。其灰度分布和直方图值如下:

现要求变换该直方图,以便使其具有表3.2第2列规定的值:

第一步,利用式(3.3-13)计算该输入图像均衡后的sk值,四舍五入后可以得到输入图像和均衡化图像的映射关系,sk中的k即为输入图像的对应灰度值:

第二步,利用式(3.3-14)计算表3.2中第2列的值计算规定直方图与均衡化后图像灰度值sk的映射关系,四舍五入后可以得到:

即得到sk(G(zq))和zq的映射关系:
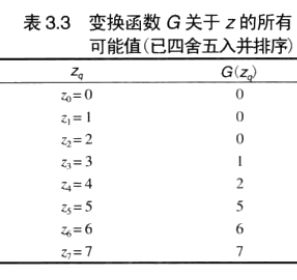
这儿有个问题,为什么sk为2的值被替换为了3?老猿才开始以为是印刷问题,看了英文原版也是3。仔细思考了下,终于理解了,相关介绍老猿在《数字图像处理:直方图匹配或规定化Histogram Matching (Specification)原理及感悟》中进行了介绍。
得到表3.4以后,我们使用表中的映射把直方图均衡后的图像中的每个像素映射为新创建的直方图规定化图像中的相应像素,这样得到的结果直方图的值列在表3.2的第三列。由于sk值为2的值被替换为了3,导致最终结果并不完全与规定直方图匹配,但达到了将输入图像灰度朝指定灰度高度近似的效果。
上述处理步骤中,得到直方图均衡后图像的中间步骤有助于解释该匹配过程,但这个步骤不是必须的,只需要得到r到s的映射和s到z的映射,然后用这些映射把原始像素直接映射到直方图规定化后的图像像素即可。
2.3.4、直方图均衡与直方图匹配案例对比

上图3.23(a)显示了火星卫星(Phobos)图像,该图像由 NASA 的火星表面探测器拍摄。图3.23(b)显示了图3.23(a)的直方图。图像的大部分是暗色区域,产生了像素集中于灰度级暗端的直方图的特点。乍看之下,会得到直方图均衡化是增强该图像的一个好办法的结论,以便使暗区域的细节更清楚。下面的讨论将证明事实并非如此。

上图3.24(a)显示了由图3.23(b)所示直方图得到的直方图均衡变换[式(3.3-8)或式(3.3-13)]。这个变换函数最相关的特征是它从灰度0快速上升到接近190。这是因为输人直方图中有大量的像素灰度接近0。当这种变换应用于输入图像的灰度,以获得直方图的均衡效果时,最终结果是把非常窄的暗像素区间映射到输出图像灰度级的高端。因为输入图像的大量像素在此暗像素区间有精确的灰度值,所以我们希望结果是具有明亮、“冲淡”(washed-out)外观的图像。如图3.24(b)所示,情况确实如此。该图像的直方图示于图3.24©。注意,所有灰度级基本上都偏向了灰度范围的上半部。
由于图3.24(a)中变换函数的问题是由原图像中大量灰度接近于0的像素引起的,一种合理的方法是修改图像的直方图,以便使其不再有这一属性。

图3.25(a)显示了一个人为规定的函数,该函数保持了原有直方图(图3.23(b))的基本形状,但在图像灰度暗区的灰度值却有更平滑的过渡。将这个函数取样为256个等间隔
的离散值,就生成了所需的规定的直方图。
使用式(3.3-14)从这一直方图得到的变换函数G(z),该变换在图3.25(b)中标注为变换(1)。类似地,由式(3.3-16)(使用前面讨论的逐步过程得到)导出的反变换函数G-1(s)在图3.25(b)中标注为变换(2)。
图3.25©中增强后的图像是把变换(2)用于图3.24(b)中直方图均衡化后的图像的像素得到的。比较这两幅图像可以看出,在使用直方图均衡得到的结果的基础上,直方图规定化图像的改进是很明显的。
注意,原始直方图的细小改变会使图像的外观得到显著改进。图3.25(d)显示了图3.25©的直方图。该直方图最容易辨别的特征是其低端已向右移向灰度级的较亮区域(但并不过分),这正是我们所希望的。
三、小结
本文介绍了连续图像和数字图像直方图匹配(直方图规定化)的原理、处理过程,并提供了案例进行了讲解。可以看到,直方图均衡处理是直方图匹配的一个重要桥梁。
到目前为止,虽然我们对直方图规定化已经很清楚了,但在结束这一节之前,我们要强调直方图规定化在大多数时候都是试错(trial-and-error)过程。这正像前边的例子中我们所做的那样,一个可用的指导路线是用手边的问题学习。但是,有时可能会遇到这样的情况,即定义“平均”直方图的外观,并把它作为规定的直方图。在这种情况下,直方图规定化就变成了一种直接的处理。然而,一般来说,并没有规定直方图的规则,对于任何一个给定的增强任务都必须借助于实际分析。
最后,对于直方图规定化这个翻译个人觉得很low,个人感觉叫指定直方图更好理解,但Histogram Specification怎么翻译确实不太好把握,因此还是叫Histogram Matching直方图匹配最好。
更多直方图处理相关知识请参考《《数字图像处理》第三章学习总结感悟2:直方图处理》。
更多图像处理请参考专栏《OpenCV-Python图形图像处理》及《图像处理基础知识》的介绍。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《 专栏:Python基础教程目录》从零开始学习Python。
如对文章内容存在疑问或需要相关资料,可在博客评论区留言,或关注:老猿Python 微信公号发消息咨询,可通过扫描二维码加微信公众号。
![]()
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
关于老猿的付费专栏
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_9607725.html 使用PyQt开发图形界面Python应用》专门介绍基于Python的PyQt图形界面开发基础教程,对应文章目录为《 https://blog.csdn.net/LaoYuanPython/article/details/107580932 使用PyQt开发图形界面Python应用专栏目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10232926.html moviepy音视频开发专栏 )详细介绍moviepy音视频剪辑合成处理的类相关方法及使用相关方法进行相关剪辑合成场景的处理,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/107574583 moviepy音视频开发专栏文章目录》;
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10581071.html OpenCV-Python初学者疑难问题集》为《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的伴生专栏,是笔者对OpenCV-Python图形图像处理学习中遇到的一些问题个人感悟的整合,相关资料基本上都是老猿反复研究的成果,有助于OpenCV-Python初学者比较深入地理解OpenCV,对应文章目录为《https://blog.csdn.net/LaoYuanPython/article/details/109713407 OpenCV-Python初学者疑难问题集专栏目录 》
- 付费专栏《https://blog.csdn.net/laoyuanpython/category_10762553.html Python爬虫入门 》站在一个互联网前端开发小白的角度介绍爬虫开发应知应会内容,包括爬虫入门的基础知识,以及爬取CSDN文章信息、博主信息、给文章点赞、评论等实战内容。
前两个专栏都适合有一定Python基础但无相关知识的小白读者学习,第三个专栏请大家结合《https://blog.csdn.net/laoyuanpython/category_9979286.html OpenCV-Python图形图像处理 》的学习使用。
对于缺乏Python基础的同仁,可以通过老猿的免费专栏《https://blog.csdn.net/laoyuanpython/category_9831699.html 专栏:Python基础教程目录)从零开始学习Python。
如果有兴趣也愿意支持老猿的读者,欢迎购买付费专栏。
