【论文阅读】GRACE:Deep Graph Contrastive Representation Learning
代码链接:https://github.com/CRIPAC-DIG/GRACE
目录
- 摘要
- 1 引言
- 2 GRACE
-
- 2.1 准备工作
- 2.2 节点表示的对比学习
-
- 2.2.1 对比学习框架
- 2.2.2 视图生成
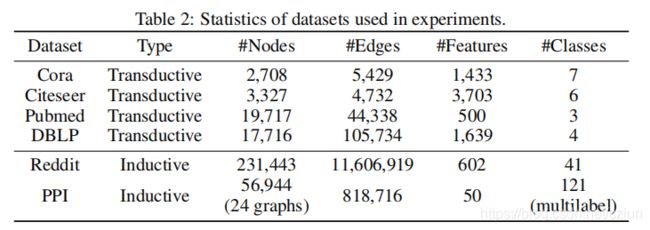
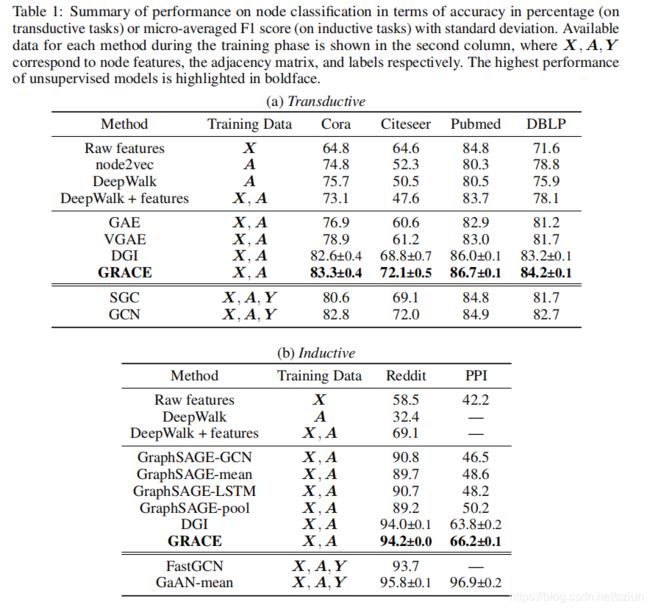
- 3 实验
摘要
本文提出了一个利用节点级对比目标的无监督图表示学习框架。
具体来说,我们通过corruption生成两个视图,并通过最大化这两个视图中节点表示的一致性来学习节点表示。
为了为对比目标提供不同的节点上下文,我们提出了一种在结构和属性层次上生成视图的混合方案。
此外,我们从互信息和三元组损失( triplet loss)两个角度提供了理论证明。
我们使用真实的数据集对transductive和inductive学习任务进行了实验。
1 引言
- DGI使用 mean-pooling readout 函数,不能保证图嵌入可以从节点中提取有用的信息,因为它不足以从节点级嵌入中保存独特的特征。
- DGI使用特征变换来生成损坏视图。然而,该方案在生成负节点样本时,在粗粒度级别考虑损坏节点特征。当特征矩阵稀疏时,只执行特征变换不足以为损坏图中的节点生成不同的邻域(即上下文),导致对比目标的学习困难。
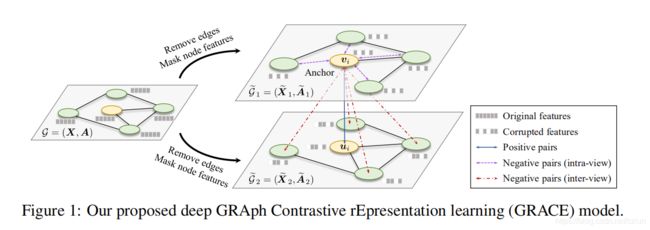
在GRACE中,我们首先通过随机执行损坏来生成两个相关的视图。
然后,我们使用对比损失来训练模型,以最大限度地提高这两个视图中节点嵌入之间的一致性。在我们的工作中,我们共同考虑拓扑和节点属性级别的损坏,即去除边和掩蔽特征,为不同视图中的节点提供不同的上下文,从而促进对比目标的优化。
最后,我们提供了理论分析,揭示了从我们的对比目标与互信息和经典的三元组损失的联系。
2 GRACE
2.1 准备工作
G = ( V , E ) \mathcal{G}=(\mathcal{V},\mathcal{E}) G=(V,E), V = { v 1 , v 2 , . . . , v N } \mathcal{V}=\{v_1,v_2,...,v_N\} V={v1,v2,...,vN}, E ⊆ V × V \mathcal{E} ⊆\mathcal{V}×\mathcal{V} E⊆V×V。
特征矩阵: X ∈ R N × F \pmb{X}∈\mathbb{R}^{N×F} XXX∈RN×F,其中 x i ∈ R F \pmb{x}_i∈\mathbb{R}^F xxxi∈RF。
邻接矩阵: A ∈ { 0 , 1 } N × N \pmb{A}∈\{0,1\}^{N×N} AAA∈{0,1}N×N,当 ( v i , v j ) ∈ E (v_i,v_j)∈\mathcal{E} (vi,vj)∈E时, A i j = 1 \pmb{A}_{ij}=1 AAAij=1。
在训练过程中,没有给 G \mathcal{G} G的节点类别信息。
我们的目标是学习一个GNN编码器 f ( X , A ) ∈ R N × F ′ f(\pmb{X},\pmb{A})∈\mathbb{R}^{N×F'} f(XXX,AAA)∈RN×F′,输入图的特征和结构,输出低维节点嵌入,即 F ′ < < F F'<
将 H = f ( X , A ) \pmb{H}=f(\pmb{X},\pmb{A}) HHH=f(XXX,AAA)作为节点学习到的表示,其中 h i \pmb{h}_i hhhi是节点 v i v_i vi的嵌入。这些表示可以用于下游任务中,如节点分类。
2.2 节点表示的对比学习
2.2.1 对比学习框架
在GRACE模型中,每次迭代生成两个视图,分别为 G 1 G_1 G1和 G 2 G_2 G2,生成的两个视图中的节点嵌入为 U = f ( X ~ 1 , A ~ 1 ) \pmb{U}=f(\widetilde{\pmb{X}}_1,\widetilde{\pmb{A}}_1) UUU=f(XXX 1,AAA 1)和 V = f ( X ~ 2 , A ~ 2 ) \pmb{V}=f(\widetilde{\pmb{X}}_2,\widetilde{\pmb{A}}_2) VVV=f(XXX 2,AAA 2),其中 X ~ ∗ \widetilde{\pmb{X}}_* XXX ∗和 A ~ ∗ \widetilde{\pmb{A}}_* AAA ∗是这些视图的特征矩阵和邻接矩阵。
然后,我们使用一个对比目标(即一个鉴别器),来区分这两个不同视图中同一节点的嵌入和其他节点的嵌入。对于任何节点 v i v_i vi,它在一个视图中生成的嵌入 u i \pmb{u}_i uuui被视为anchor,在另一个视图中生成的节点嵌入 v i \pmb{v}_i vvvi为正样本,在两个视图中除 v i v_i vi以外的节点的嵌入【假设有 M M M个节点,则负样本为 ( 2 M − 2 ) (2M-2) (2M−2)个】自然被视为负样本。定义 θ ( u , v ) = s ( g ( u ) , g ( v ) ) \theta(\pmb{u},\pmb{v})=s(g(\pmb{u}),g(\pmb{v})) θ(uuu,vvv)=s(g(uuu),g(vvv)),其中 s s s为余弦相似度, g g g是一个非线性映射——两层的MLP,以增强表达能力。
我们将每个正对 ( u i , v i ) (\pmb{u}_i,\pmb{v}_i) (uuui,vvvi)的成对目标定义为:

其中, 1 [ k ≠ i ] ∈ { 0 , 1 } 1_{[k≠i]}∈\{0,1\} 1[k=i]∈{0,1},当 k ≠ i k≠i k=i时,它等于 1 1 1。 τ τ τ是一个温度参数。
另一个视图的loss表示为 l ( v i , u i ) \mathcal{l} (\pmb{v}_i,\pmb{u}_i) l(vvvi,uuui)。
最终要最大化的总体目标定义为所有正对的平均值:
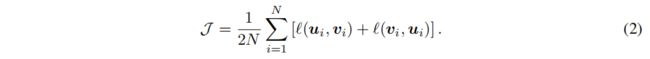
学习算法总结如下:

2.2.2 视图生成
我们设计了两种图损坏的方法——去除拓扑的边和掩盖节点属性的特征。
(1)Removing edges (RE)
我们在原始图中随机地删除一部分边。
形式上,由于我们只删除现有的边,我们首先采样一个随机掩蔽矩阵 R ~ ∈ { 0 , 1 } N × N \widetilde{\pmb{R}}∈\{0,1\}^{N×N} RRR ∈{0,1}N×N,如果原始图 A i j = 1 \pmb{A}_{ij}=1 AAAij=1,则它的值来自伯努利分布 R ~ i j ∼ B ( 1 − p r ) \widetilde{\pmb{R}}_{ij}∼\mathcal{B}(1-p_r) RRR ij∼B(1−pr),否则 R ~ i j = 0 \widetilde{\pmb{R}}_{ij}=0 RRR ij=0。这里的 p r p_r pr是每条边被删除的概率。所得到的邻接矩阵可以计算为
![]()
其中, ( x ◦ y ) i = x i y i (x ◦y)_i=x_iy_i (x◦y)i=xiyi是哈达玛积(Hadamard product)。
(2)Masking node features (MF)
除了去除边外,我们还在节点特征中用零随机屏蔽部分维度。
形式上,我们首先对随机向量 m ~ ∈ { 0 , 1 } F \widetilde{\pmb{m}}∈\{0,1\}^F mmm ∈{0,1}F进行采样,其中它的每个维度都独立地从概率为 1 − p m 1-p_m 1−pm的伯努利分布中提取,即 m ~ i ∼ B ( 1 − p m ) \widetilde{m}_i∼\mathcal{B}(1-p_m) m i∼B(1−pm)。然后,生成的节点特征 X ~ \widetilde{\pmb{X}} XXX 为:
![]()
其中, [ ⋅ ; ⋅ ] [ ·; ·] [⋅;⋅]是连接操作。
请注意,虽然我们提出的RE和MF方案在技术上与Dropout和DropEdge相似,但我们的GRACE模型和这两种方法的目的存在根本不同。Dropout是一种通用的技术,它在训练期间随机屏蔽神经元,以防止大规模模型的过拟合。在图域中,提出了DropEdge来防止GNN体系结构过深时的过拟合和缓解过平滑。然而,我们的GRACE框架随机应用RE和MF生成图拓扑和节点特征层次的对比学习图。此外,在GRACE中使用的GNN编码器是一个相当浅的模型,通常只包含两到三层。
在我们的实现中,我们共同利用这两种方法来生成视图。 G ~ 1 \widetilde{\mathcal{G}}_1 G 1和 G ~ 2 \widetilde{\mathcal{G}}_2 G 2的生成由两个超参数 p r p_r pr和 p m p_m pm控制。为了在这两个视图中提供不同的上下文,这两个视图的生成过程使用了两组不同的超参数 p r , 1 p_{r,1} pr,1、 p m , 1 p_{m,1} pm,1和 p r , 2 p_{r,2} pr,2、 p m , 2 p_{m,2} pm,2。实验表明,我们的模型在温和的条件下对 p r p_r pr和 p m p_m pm的选择不敏感,因此原始图没有过度损坏,例如, p r ≤ 0.8 p_r≤0.8 pr≤0.8和 p m ≤ 0.8 p_m≤0.8 pm≤0.8。