空间分析（二）——统计进阶

格局分析

Join count统计

当空间随机变量是类型变量的时候，用Join-count方法来计算空间自相关，即评价空间离散/聚集程度。
Join-count是全局统计方法

• 理论依据：
  考虑只有两种类型的变量，绿色出现的概率为$P_1$，则白色出现的概率为$1-P_1$
  绿绿连在一起的概率：$P_{GG}=P_1{P}_1=P_1^2$
  白白连在一起的概率：$P_{WW}=\left(1-P_1\right)\left(1-P_1\right)={\left(1-P_1\right)}^2$
  白绿交叉出现的概率：$P_{GW}=P_B\left(1-P_1\right)+\left(1-P_1\right)P_1=2P_1\left(1-P_1\right)$
  理论随机值： 概率乘上邻接矩阵并加权求和，得到的结果即为在随机情况下这表现出某种关系的单元在空间中出现的期望。
  $E=\frac{1}{2}{\sum }_i{\sum }_j{w}_{ij}P$

  实际值：$GG=\frac{1}{2}{\sum }_i{\sum }_j{w}_{ij}{y}_i{y}_j$ （Green）
  $y_j$：为绿色时记为 1，为白色时记为 0。

  然后通过Z-Scores检验实际值是否显著高于/低于随机下的期望值，从而来判断是否存在空间自相关。
  

Lacunarity analysis

定义： 孔隙分析是一种描述空间离散模式的多尺度方法。用来判别与空间纹理相关的对象的分布模式，计算结果具有尺度依赖性。
基本思想： 利用 ”gliding box” 扫描目标研究区域，并计算 Lacunarity统计量，然后通过分析Lacunarity统计量随之gliding box大小的变化情况，得出研究区某随机变量的空间分布随着观测尺度变化的特征。

Lacunarity统计量：
$r$：box的大小（观测尺度）；
$s$：box里变量的数目
$n(s,r)$：frequency distribution of the box masses（计数序列）
$N(r)$：total number of boxes of size $r$（总数）
$Q(s,r)$：$=n(s,r)/N(r)$，概率分布

该分布的一阶和二阶原点矩：
$Z(1)=\Sigma sQ(s,r)$，=均值：$\bar{s}(r)$
$Z(2)=\Sigma s^{2}Q(s,r)$，=方差+均值平方：$s_s^2(r)+{\bar{s}}^2(r)$

根据上述内容，将Lacunarity统计量定义为：
$$\Lambda (r)=s_s^2(r)/{\bar{s}}^2(r)+1$$
解释：
当窗口 $r$ 的大小固定时，分布的越聚集（sparse），方差越大，均值越小，Lacunarity值越大。所以，越高的值意味着越强的聚集效应存在。
观测尺度增大，或是观测对象的聚集程度减少，Lacunarity降低，极值趋向1
与随机模式下的尺度-值的变化相比，得出是否存在特殊的分布模式，以及是否显著的结论

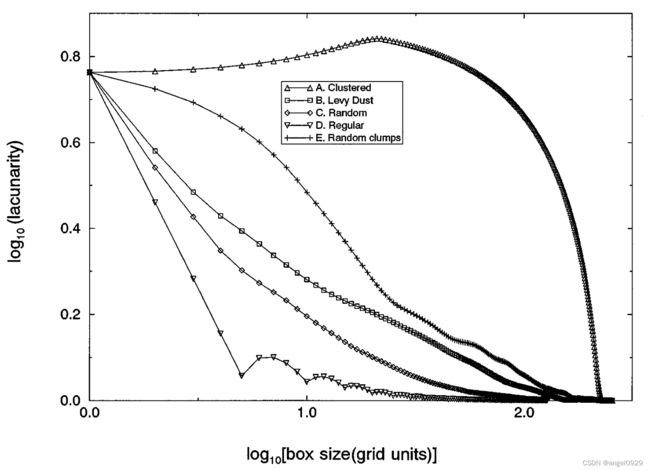
Set A： 当box远远小于序列长度（M）的时候，大部分的box要么被元素完全充满，要不然是全空状态。所以方差很大，Lacunarity值很大。当box大小达到聚集块的大小时，Lacunarity值快速下降。
Set D： 完全均匀分布的状态，元素之间的间隔固定，大小为M/S，所以每一个box中的元素数目 $s$ 的值是恒定的。所以方差趋于0，同时，当box的大小超过M/S时，Lacunarity的值趋于1。
Set C： 随机分布形成了一个向上的凹曲线，在box大小很小时急剧下降。在box变大后方差趋于平稳，Lacunarity值平稳下降。这是因为随机模式在更大范围内具有统计不变性。
Set B： Levy dust的值在所有box的情况下都高于随机序列。是因为它具有层次聚集性（hierarchically clumped）<我理解的是在一定的尺度下，Levy dust分布呈现聚集>。这种分布又被称为分形分布（fractal distribution）
Set E： 曲缓慢下降到约Lacunarity值约为0.6的点，这一点对应的box size与聚集块的大小相近。之后曲线迅速下降，曲线走势与随机分布模式相似。

Centrography 点模式分析

点分析的内容：

• 点的数量，多少
• 点的疏密，分布是均匀、随机、聚集？
• 点的方位，点分布的方向和范围
• 点的属性：有哪些性质
• 其它：如动态变化等

密度分析

• 分布密度：
  $\hat{\lambda }=\frac{n}{a}=\frac{\#(S\in A)}{a}$
  $n$ 为选定尺度下分布对象的计量；$a$ 为分布区域的计量。

• 样方分析
  该方法通过检查其密度(每个样方的点数)在空间上的变化来评估点分布。
  步骤：
  （1）将研究区域划分为规则的正方形格网
  （2）统计待评价模式下各样方中的点数目，得到相应的频率分布
  （3）将该频率分布与已知模式（通常是构造得到的随机分布）的频率分布进行比较，来待评价的模式与随机模式相比是更分散还是更聚集。

  用${\chi }^2$检验法对这些数据进行估计，其公式表示为：${\chi }^2=\sum (Q-E{)}^2/E$
  $Q$为每个样方中实际点数量；$E$为已知模式（均匀分布、随机分布）下的期望值。
  ${\chi }^2$越大，待评价分布与已知分布相符的可能性越小

方位分析

中心位置

标准差椭圆

绘制方法：
（1）确定圆心

$\begin{array}{rl}SD{E}_x& =\sqrt{\frac{{\sum }_{i=1}^n{\left(x_i-\bar{X}\right)}^2}{n}}\\ SD{E}_y& =\sqrt{\frac{{\sum }_{i=1}^n{\left(y_i-\bar{Y}\right)}^2}{n}}\end{array}$

$X_i$ 和 $Y_i$ 是每个要素的空间位置坐标，$\bar{X}$ 和 $\bar{Y}$是算数平均中心。

$SD{E}_x$ 和 $SD{E}_y$就是计算出来的椭圆的方差。
椭圆的大小取决于方差大小，长半轴表示最大方差，短半轴表示最小方差，在空间统计上面，用X、Y的方差进行计算，得到长短半轴。

（2）确定椭圆的方向

$\begin{array}{rl}\tan \theta & =\frac{A+B}{C}\\ A& =\left(\sum _{i=1}^n{\tilde{x}}_i^2-\sum _{i=1}^n{\tilde{y}}_i^2\right)\\ B& =\sqrt{{\left(\sum _{i=1}^n{\tilde{x}}_i^2-\sum _{i=1}^n{\tilde{y}}_i^2\right)}^2+4{\left(\sum _{i=1}^n{\tilde{x}}_i{\tilde{y}}_i\right)}^2}\\ C& =2\sum _{i=1}^n{\tilde{x}}_i{\tilde{y}}_i\end{array}$

${\tilde{x}}_i$、${\tilde{y}}_i$是平均中心和(x, y)坐标的差

（3）确定椭圆方程

${\sigma }_x=\sqrt{2}\sqrt{\frac{{\sum }_{i=1}^n{\left({\tilde{x}}_i\cos \theta -{\tilde{y}}_i\sin \theta \right)}^2}{n}}$
${\sigma }_y=\sqrt{2}\sqrt{\frac{{\sum }_{i=1}^n{\left({\tilde{x}}_i\sin \theta +{\tilde{y}}_i\cos \theta \right)}^2}{n}}$

${\left(\frac{x}{{\sigma }_x}\right)}^2+{\left(\frac{y}{{\sigma }_y}\right)}^2=s$

${\sigma }_x$、${\sigma }_y$分别是X、Y轴的标准差
$s$ 是置信度的值

结果解读：
（1）椭圆的长半轴表示的是数据分布的方向，短半轴表示的是数据分布的范围，长短半轴的值差距越大（扁率越大），表示数据的方向性越明显。
（2）短半轴表示数据分布的范围，短半轴越短，表示数据呈现的向心力越明显；反之，短半轴越长，表示数据的离散程度越大。
（3）若长短半轴相等，则表示数据没有任何的分布和方向特征。

标准差的体现：
三个级别的椭圆，分别表示生成的椭圆能够包含68%，95%和99%的数据，对应着标准正态分布中的$1\sigma$，$2\sigma$，$3\sigma$。

属性分析

• 空间插值
• 空间聚类
• 空间相关性分析
• ……

其它

• 趋势变化
• 轨迹追踪
• ……

完全空间随机性（Compete Spatial Randomness -CSR）

两个特征：
1、空间一致性：
每一个位置发生某一件事情具有相同的概率，事件的强度在平面上并不发生变化
2、独立性：
两个地点是否发生某一事件不相互影响

The events of a pattern are independently and uniformly distributed over space; in other words, the events are equally likely to occur anywhere and do not interact with each other.

数学定义：
考虑一个区域S及其子区域C。S中有n个随机点，$N(C)$表示落在区域C内的点个数。

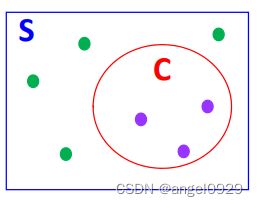
则$N(C)$在随机下的期望为：

$E[N(C)]=n\frac{a(C)}{a(S)}$

将S的点落在C内视作一个随机实验，则落在C内的点的个数的概率分布满足二项分布，即某件事情发生概率为$p,p=\frac{a(C)}{a(S)}$，那么

$P(\mathrm{X}=k)=C_n^k{p}^k(1-p{)}^{n-k}$
带入$p$可进一步计算出有k个点落在区域C中概率

当$n$趋于∞时，上时采用泊松分布近似，另$\lambda =\frac{n}{a(S)}$，则：

$P[N(C)=k\mid \lambda ]=\frac{[\lambda a(\mathrm{C}){]}^k}{k!}{e}^{-\lambda a(\mathrm{C})}$

应用：
（1）用作零假设，来判断点分布是否为随机的

检验方法：${\chi }^2$检验（O为实际值，E为CSR模式下的期望值）

因为泊松分布的方差和均值相等，所以在CSR的情况下，方差均值之比为1。所以>1：离散分布；<1：聚集分布。

（2）判断当处在在某一位置上时，下一个有事件发生的点与该位置的距离是多少

记随机变量D为给定点到离其最近点的距离，则D在CSR下的分布为：

$P\{D<d\}=P\left\{N\left[a\left(C_d\right)\right]=k=0\right\}=e^{-\lambda a\left(C_d\right)}=e^{-\lambda \pi d^2}$
$P\{D=d\}=p(d)=F^{\prime }(d)=2\pi \lambda d\cdot e^{-\pi \lambda d^2}$

再根据大数定理构造标准正态分布，进行Z-test检验。
$Z_m=\frac{{\bar{D}}_m-1/(2\sqrt{\lambda })}{\sqrt{(4-\pi )/(m4\pi \lambda )}}$

点过程的协变量效应

趋势分析

趋势分析是分析地理现象沿着时间/空间变化的规律
常见的模型分类：

• 线性 or 非线性
• 参数 or 非参数

线性趋势

一般用简单线性回归拟合
拟合方程： $y_t=a+bt$
用最小二乘法拟合求解未知参数$a$、$b$

线性显著性检验：

（t分布的自由度为n-2）

单调趋势

随着时间/空间存在上升/下降的改变, 通常只关心相对大小，并且对异常值不敏感，

判断平均变化趋势的大小：（Sen‘’s估计法）
$\beta =\mathrm{Median}\left(\frac{x_{\mathrm{j}}-x_{\mathrm{i}}}{\mathrm{j}-\mathrm{i}}\right),\mathrm{j}>\mathrm{i}$

显著性检验：
Mann-Kendall趋势检验： 一种非参数检验方法，能检验某一自然过程是处于随机波动还是存在确定的单调改变
趋势。不需要样本遵从一定的分布，只关心观测值的相对大小。

统计量：
$S={\sum }_{k=1}^{n-1}{\sum }_{j=k+1}^n\mathrm{sign}\left(x_j-x_k\right)$
随机情况下的期望和方差：
$\mathrm{E}(\mathrm{S})=0$
$Var(\mathrm{S})=\mathrm{n}(\mathrm{n}-1)(2\mathrm{n}+5)/18$
检验统计量：
n>10的时候根据大数定理转换为标准正态分布。
$\mathrm{Z}=\{\begin{array}{cl}\frac{\mathrm{S}-1}{\sqrt{\mathrm{Var}(\mathrm{S})}}& \mathrm{S}>0\\ 0& \mathrm{S}=0\\ \frac{\mathrm{S}+1}{\sqrt{\mathrm{Var}(\mathrm{S})}}& \mathrm{S}<0\end{array}$

随机性和断点检验

随机性检验

方法

• Wallis-Moore Phase Frequency Test
• Bartels rank von Neumann’s ratio test
• Wald-Wolfowitz Test
• ……

Wald-Wolfowitz Test：
统计量：
$R={\sum }_{i=1}^{n-1}{x}_i{x}_{i+1}+x_1{x}_n$
随机情况下的期望和方差：
$E(R)=\frac{s_1^2-s_2}{n-1}$
$V(R)=\frac{s_2^2-s_4}{n-1}-E(R{)}^2+\frac{s_1^4-4s_1^2{s}_2+4s_1{s}_3+s_2^2-2s_4}{(n-1)(n-2)}$

$s_t={\sum }_{i=1}^n{x}_i^t,t=1,2,3,4$

检验统计量
n>10的时候根据大数定理，可以用正态分布近似拟合。

$Z=\frac{R-E(R)}{\sqrt{V(R)}}$

突变点检测

方法

• Lanzante’s test procedures
• Pettitt’s test, Buishand Range Test
• Buishand U Test
• Standard Normal Homogeneity Test
• ……

Buishand U Test：
步骤：
（1）将样本分成两段：
$x_i=\{\begin{array}{ll}\mu +{ϵ}_i,& i=1,\dots ,m\\ \mu +\Delta +{ϵ}_i& i=m+1,\dots ,n\end{array}$

（2）$H_0：\Delta =0$

（3）构造统计量：
$U=$ $\frac{1}{n(n+1)}$ ${\sum }_{k=1}^{n-1}{\left(S_k/D_x\right)}^2$

$S_k={\sum }_{i=1}^k\left(x_i-\bar{x}\right)1\le i\le n$， $D_x=\sqrt{n^{-1}{\sum }_{i=1}^n{\left(x_i-\bar{x}\right)}^2}$

P-value由Monte Carlo模拟求得
$\hat{S}=\max \left(\left|S_k\right|\right)$，突变点K为$\left|S_k\right|$最大时对应的 k 值

空间插值

暂略

描述统计量

距离与相似性

（Comprehensive Survey on Distance/Similarity Measures between Probability Density Functions）

1. 连续数值变量

   ${\left({\sum }_{i=1}^n{\left|x_i-y_i\right|}^p\right)}^{1/p}$
   $p=2$，欧式距离
   $p=1$，曼哈顿距离
   ……

2. 二值变量
   
   symmetric binary variables：$d(i,j)=\frac{b+c}{a+b+c+d}$

   asymmetric binary variables： $d(i,j)=\frac{b+c}{a+b+c}$

3. 类型变量

   $d(i,j)=\frac{p-m}{p}$，（p：变量总数，m：两个实体相同的变量数）

4. 顺序变量

   $z_{if}=\frac{r_{if}-1}{M_f-1}$，（$r_{if}$：变量的顺序，$M_f：$变量总数）

多样性

多样性指数定量测量在同一集合(区域)内，有多少种不同类型的对象以及每种类型对象数量的分布特征。

衡量方法：

• Shannon entropy，熵：
  $H^{\prime }=-{\sum }_{i=1}^R{p}_i\ln p_i$，（R是类型个数，p是每种类型的比例）

• Simpson index：
  $\lambda ={\sum }_{i=1}^R{p}_i^2$

• Gini–Simpson index：
  $1-\lambda =1-{\sum }_{i=1}^R{p}_i^2$

Simpson index和GIni-Simpson index的实际含义是随机选取两个目标，类型相同/不同的概率

不均衡系数

Gini系数： 最初用于描述一个区域内收入/财富在人群中的分布以及不均衡性评估
定义： Gini系数的定义是基于Lorenz曲线：$G=\frac{A}{A+B}$

应用：

• 环境领域：用来衡量生物多样性，其中作对比的是物种的累积比例与个体的累积比例。
• 健康领域：用于衡量人口中与健康有关的生活质量的不平等程度。
• 教育领域：用来衡量大学的不平等程度。
• 工程应用，用于评估Internet routers在调度来自不同流量的数据包传输时所达到的公平性。
• ……

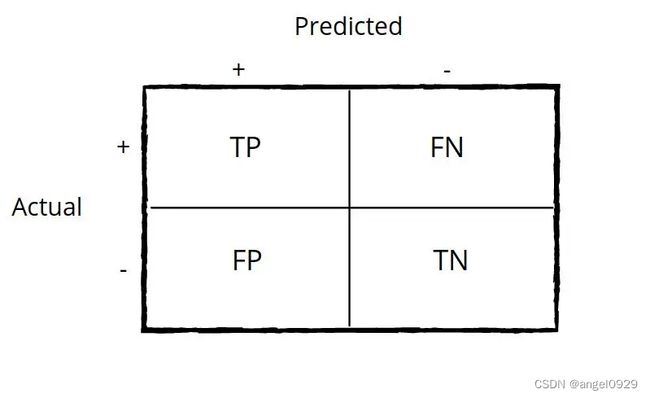
混淆矩阵相关内容

基本概念：

• Accuracy（准确性）：
  $(TP+TN)/total$
  用于总体评价模型分类的准确性如何，在样本均衡的时候是一个合理有效的评价指标，当样本不均衡时不好用。
  eg.
  
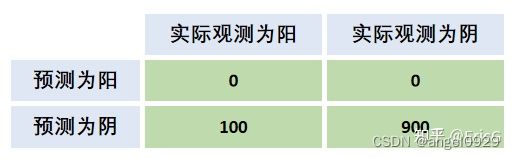
  该模型的Accuracy达到0.9。但是实际上，模型一个阳性都没有鉴别出来。

• True Positive Rate（召回率）
  $=TP/TP+FN$
  又被称为Sensitivity，Recall，是指目标对象被正确识别的比例。
  追求TPR高可以解释为“不放过一个坏人”，极端情况为将所有对象都预测为目标对象，此时 TPR= 1。

• True Negative Rate（特异性）
  $=TP/FP+TN$
  又被称为Specificity，是指非目标对象被正确排除的比例。
  追求TNR高可以解释为“不冤枉一个好人”，极端情况为把所有对象都预测为非目标对象，此时 TNR = 1。

• Precision（精度）
  $=TP/TP+FP$
  在被识别为目标对象的集合中有多少是真正的目标对象。
  1-Precision可以用来表示“有多少好人被冤枉”。同理，1-$TN/TN+FN$可以用来表示“有多少坏人被放过”。

• Error Rate（错误率）
  $=(FP+FN)/total$

Kappa系数

用来弥补用Accuracy评价模型时由于样本不均衡而产生的不合理性。根据Kappa系数的计算公式，越不平衡的混淆矩阵，$p_e$越高，Kappa值就越低，从而可以给“偏向性”强的模型打低分。
用于一致性检验，可以用于多分类问题。
$$K=\frac{{\mathrm{P}}_{\mathrm{o}}-{\mathrm{P}}_{\mathrm{e}}}{1-{\mathrm{P}}_{\mathrm{e}}}$$
$p_o=\frac{\text{ 对角线元素之和 }}{\text{ 整个矩阵元素之和 }}$，$p_e=\frac{{\sum }_i\text{ 第 }i\text{ 行元素之和 }\ast \text{ 第 }i\text{ 列元素之和 }}{{\left(\sum \text{ 矩阵所有元素 }\right)}^2}$

$F$ Score

是一个综合考虑 Precision 和 Recall 的评估指标，理想情况下是希望两个指标都高，但实际情况是Precision高，Recall就低，Recall高，Precision就低。
所以我们需要一个综合的指标对两个值进行折中与取舍：
（1）在保证召回率的条件下，尽量提升精确率（一般的搜索情况）
（2）在保证精确率的条件下，尽量提升召回率。（癌症检测、地震检测、金融欺诈）

$F-$ Score $=\left(1+{\beta }^2\right)\cdot \frac{\text{ Precision }\cdot \text{ Recall }}{{\beta }^2\cdot \text{ Precision }+\text{ Recall }}$

通过调整 β 来调节哪一个值更重要。如果认为精确率更重要些，那就调整β的值小于1；如果认为召回率更重要些，那就调整β的值大于1。

ROC曲线

用来比较在每一个阈值下，非目标对象未被排除的比例和目标对象被正确识别的比例之间的关系。
根据ROC曲线找最优点的原则就是：保证TPR高的同时FPR要尽量的小。可以建立
$max(TPR+(1-FPR))$的模型。一般方法是找到离（0,1）最近的点。

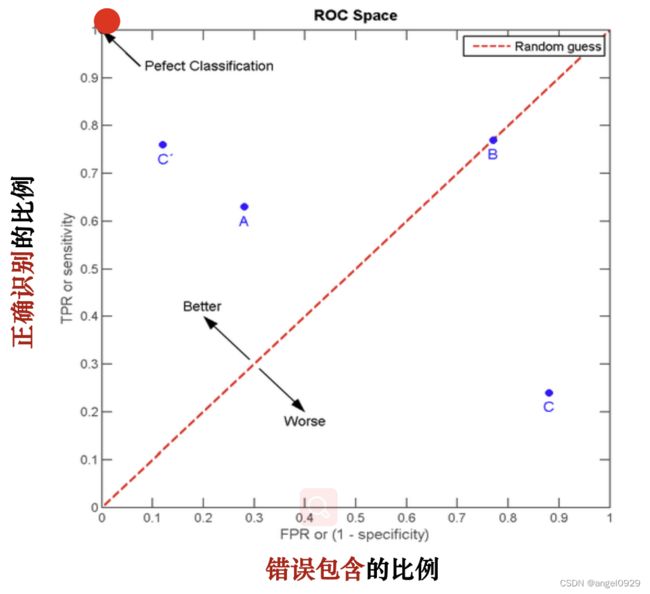
在实际应用中选取最佳阈值，还需要考虑对真阳性的要求以及对假阳性的容忍程度。
比如，在一些病毒检测实验中，要求能够识别出所有的真阳性、可以容忍一定程度的假阳性（宁可错杀三千，不可放过一个）——此时要选靠右的点的阈值，使得TPR尽可能大。
如果不能容忍假阳性、要求识别出来的样本必须为真阳性（绝不冤枉一个好人）——此时可以选靠右的点对应的阈值，使得FPR尽可能小。

AUC
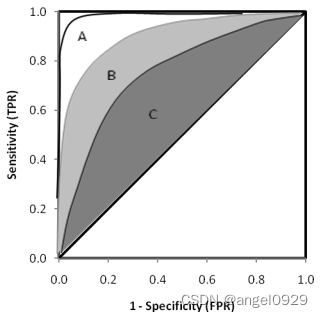
ROC曲线下的面积(AUC)衡量一个分类器随机选择一个目标对象高于随机选择非目标对象的概率。所以一般来说，AUC 的值越大表示模型越好。

上图中的三条ROC曲线，A模型比B和C都要好

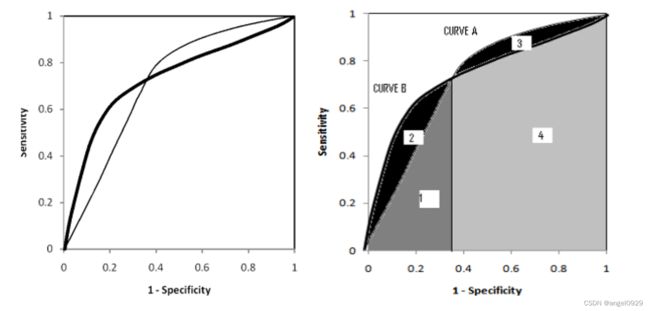
上面两幅图中两条ROC曲线相交于一点，AUC值几乎一样：
当需要高Sensitivity时，模型A比B好；
当需要高Speciticity时，模型B比A好