论文笔记：HyperNetworks（arXiv版本）

这篇博客是啥？

这篇博文是有关HyperNetworks arXiv版本的笔记，为啥选择arXiv版本呢，因为ICLR官方编辑版本有许多删减，致使我有一部分公式看不懂（可能是因为我个人才疏学浅吧）。 这篇博文主要是讲HyperNetworks的方法，不会对实验进行介绍。

---

论文地址

arXiv版本： HyperNetworks arXiv
ICLR版本：HyperNetworks ICLR_2017

---

基本思想

HyperNetworks 的基本思想是想用一个小网络(HyperNetworks)为大网络（main Networks） 生成参数， 如下图

在上图中， 橙色的方块是小网络(HyperNetworks) ， 黑色的是大网络（main Networks） 橙色点箭头是小网络为大网络生成的参数矩阵。

说明

我们平常怎么保存一个模型？根据我的经验，以上图为例，一般人会将上图中$[W_1,W_2,W_3,...,W_n]$这些权重矩阵保存下来。于是有人就想这也太浪费空间了吧，我能否找个函数使得$[z_1,z_2,z_3,...,z_n]mapping[W_1,W_2,W_3,...,W_n]$. 这里$z$的维度远小于$W$, 这种做法我只需要保存$z$和$mapping$函数就行了，这样就可以节省空间了！

---

方法

作者将HyperNetworks 分为动态的静态的两种模式

---

静态 HyperNetworks

论文中， 作者拿卷积神经网络(CNN)作为main Network。
我们假设每个卷积层：
输入的channel为 $N_{in}$ ；
卷积核size 为$f_{size}\times f_{size}$；
输出的channel 为 $N_{out}$
那么这一层的参数量为$N_{in}\times f_{size}\times f_{size}\times N_{out}$，第$j$层参数量记作 $K^j\in {\mathbb{R}}^{N_{in}{f}_{size}\times f_{size}{N}_{out}}，j\in 1,....,D$这里$D$为卷积的深度depth。
然后，作者提出了一个生成器$g$使得：
$$K^j=g(z^j),\forall j=1,...,D\text{\hspace{1em}(1)}$$
生成器$g$是一个两层的线性网络，作者首先将 $K^j\in {\mathbb{R}}^{N_{in}{f}_{size}\times f_{size}{N}_{out}}$拆分成$N_{in}$个slices,
即$K^j=conca{t}_{i=1}^{N_{in}}(K_i^j),K_i^j\in {\mathbb{R}}^{f_{size}\times f_{size}{N}_{out}},i\in 1,....,N_{in},j\in 1,....,D$
生成器$g$的公式：

这里，$z^j\in {\mathbb{R}}^{N_z},W_i\in {\mathbb{R}}^{d\times N_z}$, $d$为生成器$g$的隐藏层的size；$a_i^j\in {\mathbb{R}}^d,B_i\in {\mathbb{R}}^d,W_{out}\in {\mathbb{R}}^{f_{size}\times N_{out}{f}_{size}\times d},B_{out}\in {\mathbb{R}}^{f_{size}\times N_{out}{f}_{size}}$， 运算符<·>表示张量内积:

通过这种方法参数分别是: $$z^j:N_z\times D；W_i:d\times N_z\times N_i;B_j:d\times N_i;W_{out}:f_{size}\times N_{out}{f}_{size}\times d;B_{out}:f_{size}\times N_{out}{f}_{size}$$
总共 $$N_z\times D+d\times (N_z+1)\times N_i+f_{size}\times N_{out}\times f_{size}\times (d+1)$$
不使用HyperNetwork原参数共$D\times N_{in}\times f_{size}\times N_{out}\times f_{size}$,相比之下，使用HyperNetworks的参数大大减少了

---

动态 HyperNetworks

作者这里拿(如下图)大RNN(黑色)来作为main network,小RNN作为HyperNetworkRNN(橙色)，这里为啥叫动态呢？ 是因为RNN时序的，其参数会随时间变化。

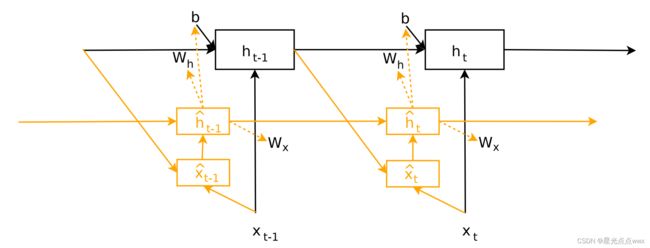
我们知道标准的RNN公式：$h_t=\varphi (W_h{h}_{t-1}+W_x{x}_t+b)$， 这里共有三个参数$W_h,W_x,b$ 需要HyperNetwork按时序生成，这就是作者为啥也用时序网络(较小的RNN)作为HyperNetwork的原因，跟静态HyperNetwork一样，作者也用生成器（线性层）生成三个参数$W_h,W_x,b$， 这里生成器分别用$W_h(z_h),W_x(z_x)，b(z_b)$表示，这里$z_h,z_x,z_b$表示时序条件（这里你可以认为生成器是一种条件GAN，或者也可以叫做解码器）。所以main RNN 的公式可以改写成：
$$\begin{gathered} h_t=\varphi (W_h(z_h)h_{t-1}+W_x(z_x)x_t+b(z_b)) \\ {W}_h(z_h)=<W_{hz},z_h> \\ {W}_x(z_x)=<W_{xz},z_x> \\ b(z_b)=W_{bz}{z}_b+b_0\text{\hspace{1em}(2)} \end{gathered}$$
这里 $W_{hz}\in {\mathbb{R}}^{N_h\times N_h\times N_z},W_{xz}\in {\mathbb{R}}^{N_h\times N_x\times N_z},W_{bz}\in {\mathbb{R}}^{N_h\times N_z},b_0\in {\mathbb{R}}^{N_h}$, 运算符 <·> 表示张量内积（多维矩阵的乘法）。
为了进一步降低存储，条件$z_h,z_x,z_b$也用线性生成器生成（对应上图的橙色的部分）：

貌似终于大功告成了！欸，等会。。 这种方法保存的线性层的权重矩阵也太多了吧！所以作者就想在
标准的RNN公式：$h_t=\varphi (W_h{h}_{t-1}+W_x{x}_t+b)$上对权重的放缩，而不是完全替换，比如说像这样$W_h^{new}=d_h(z_h)\odot W_h^{old}，W_x^{new}=d_h(z_x)\odot W_x^{old}$， 这里$\odot$表示按位乘法：

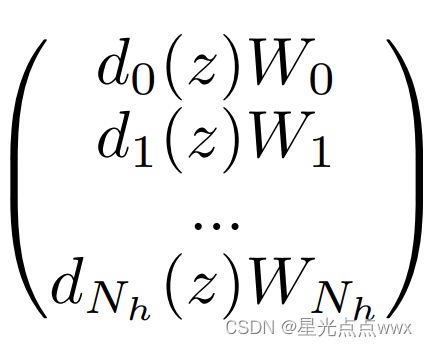
这种做法是在原有的参数矩阵上进行缩放，大大降低储存量（我只要储存$W^{old}$和一组缩放向量$d$即可），提高了内存效率，最后内存高效率版本可以写做：
（疑惑：这与之前的方法相比，必定损失一定精度）

太好了终于结束了！

---