微积分入门（持续更新）

0x00 前言

• $Wemustknow.Wewillknow.$
   ——David Hilbert

微积分（Calculus），数学概念，是高等数学中研究函数的微分（Differentiation）、积分（Integration）以及有关概念和应用的数学分支。它是数学的一个基础学科，内容主要包括极限、微分学、积分学及其应用。

微分学包括求导数的运算，是一套关于变化率的理论。它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论。积分学，包括求积分的运算，为定义和计算面积、体积等提供一套通用的方法。

1x01 微分（其一）一一瞬时变化率？极限的严格定义

想象一辆汽车，其所走过的路程 $(s)$ 和时间 $(t)$ 的关系为 $s=t^2$ ，现在要求速度 $(v)$ 与时间的关系。

我们先把问题简化一下，我们现在只求汽车在第 $5$ 秒时的瞬时速度。有头绪吗？

三——

二——

一——

好，揭晓答案。我们先把时间定位在 $5-5.1s$ 之内。在这个区间内，它的平均速度为：
$$v=\frac{s}{t}=\frac{5.1^2-5^2}{5.1-5}=\mathrm{10.1.}$$
现在我们再把时间的范围缩小到 $5-5.01s$ 之内。现在它的平均速度为：
$$v=\frac{s}{t}=\frac{5.01^2-5^2}{5.01-5}=\mathrm{10.01.}$$
$Andsoon,$ 我们继续将时间范围缩小、缩小、再缩小，我们可以看到的是，平均速度逐步 “趋近” $5$ 。

但是我们需要一个严格的证明啊！！！

因此，我们定义，对于 $t$ 的一个变化量，我们称之为 $\Delta t$ 。那么我们将 $5-5+\Delta t$ 这个时间段内的平均速度则可以表示为：
$$v=\frac{s}{t}=\frac{(5+\Delta t{)}^2-5^2}{\Delta t}=10+\Delta t.$$
现在，我们让 $\Delta t$ 变得很小，很小，非常小，小到几乎为 $0$ ，这时原式的值为 $10$ 。

现在我们用极限的记号来表示这个过程：
$$\underset{\Delta t\to 0}{\lim }\frac{(5+\Delta t{)}^2-5^2}{\Delta t}=10$$

我们也可以借此求出通用的公式：
$$v=2t$$
我们就把 $v=2t$ 称为 $s=t^2$ 的导函数，导函数在 $n$ 处的值就是原函数在 $n$ 处的导数。

$Butnow,$ 问题来了，当 $\Delta t$ 越来越小时，分母也越来越接近于 $0$ ，这该怎么办呢？这时候我们就要来看一下贝克莱怎么说：

. . . . . . 事实上我们必须意识到，牛顿使用 无穷小量 ，正如同使用建筑物的脚手架一样，一旦找到了和它们成比例的线元，便过河拆桥，将其抛弃不谈。然而这一有限的成分（当指 “线性主部” ）是借由 无穷小量 的帮助而得出的，故由此成分和比例得出的一切结论（包括微积分的一切定理与应用），都应归功于 无穷小量 ：那么这样一个概念必然是首先应该得到解释的。可是 无穷小量 是什么呢？是 “消散增量的速率” ？那这些 消散的增量 又是什么呢？它们既非 有限量 ，也不是 无限小 的量（即，比任何有限量都小的量），然而却又不是 零 。那么我们或许也只好称其为 “消逝量的幽灵” 了吧？
（注：贝克莱在原文中使用了 “Fluxions” 一词，历史上对应今天所言的 “导数” ；然而根据语境，当指用以作商的 微小增量 ，故译为 “无穷小量” ）

于是， 【第二次数学危机】 由此揭发。最后终于找到了一个令人比较满意的解答： $ϵ-\delta$ 语言。

$ϵ-\delta$ 语言指出，如果 $t$ 和 $\Delta t$ （$t$ 指原时间）相差与 $v$ 和 $v+\Delta t$ 之差为等价无穷小，则称 $v+\Delta t$ 为 $v$ 的极限。

（像是优雅的废话）

通俗一点：

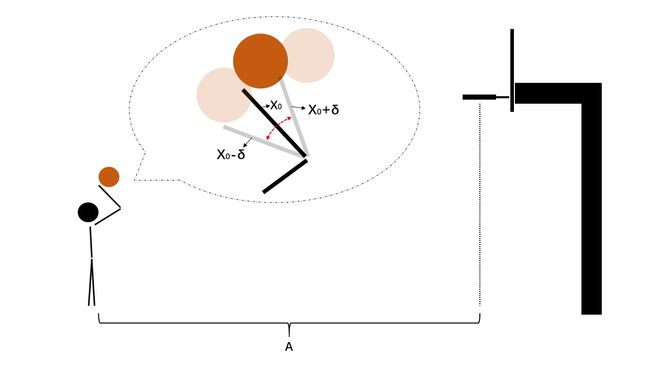
大家知道，我们投篮的时候，篮筐越大越容易进，最极端的情况就是篮筐和篮球一样大。现假设篮球在篮筐正中心时，与篮筐边缘的距离为 $ϵ$ ，如下图所示：

若投篮者与篮筐正中心的距离为 $A$，投篮者的真实投篮距离为 $f(x)$ ，如果想要将球投进，则需要满足 $|f(x)-A|<ϵ$，即投篮者的力度需要恰到好处，不能太多也不能太少，而力度所对应的便是投篮者的手部弯曲程度，只要弯曲程度在一定范围内（如下图红色范围），就可以将球投进，这个所谓的 “一定范围” ，便是去心领域, $0<|x-x_0|<\delta$ ，（如果这里 $0$ 可以取等于，则为不去心邻域），即 $x_0-\delta <x<x_0+\delta$ ，如下图所示：

（啊这迷人的画风）

而函数有极限，就相当于投篮者拥有库里的投射能力，无论 $ϵ$ 多么的小，即无论篮筐大小多么接近篮球大小，投篮者都可以找到一个精确的角度范围将球投进。由此，极限定义可通俗地写为：

对于任意大小的篮筐（无论其与篮球大小之差 $ϵ$ 多么的小），拥有 神射能力的投篮者 （对应于拥有极限的函数）总能找到一个极小的精确的投篮角度范围 $0<|x-x_0|<\delta$ ，将球投进，即投射距离 $f(x)$ 与最佳距离 $A$ 的差距小于 $ϵ$ ，即 $|f(x)-A|<ϵ$ .

因此，数学家们解决了 “无穷小的悖论” 。那么下一节，我们来学习通用的求导方法。

1x02 微分（其二）——通用的求导方式&用图像求导

现在，我们来试求 $y=x^3$ 的导数。

首先，我们令 $x$ 的增量为 $\Delta x$ ， $y$ 的增量为 $\Delta y$ ，可得：
$$y^{{}^{\prime }}=\frac{\Delta y}{\Delta x}=\frac{(x+\Delta x{)}^3-x^3}{\Delta x}=\frac{x^3+3x^2\Delta x+3x{\Delta x}^2+{\Delta x}^3-x^3}{\Delta x}$$
化简得：
$$y^{{}^{\prime }}=3x^2+3x\Delta x+\Delta x^2$$
现在，我们让 $\Delta x$ 趋近于 $0$ ，可得：
$$y^{{}^{\prime }}=3x^2.$$
你也可以试着求一下其它形如 $y=x^n$ 函数的导数，会发现结果都是 $y^{{}^{\prime }}=n{x}^{n-1}$ .其实是因为在分解时，$x^n$ 被削去了，剩下的部分只有 $n{x}^{n-1}\Delta x$ 只包含一个 $\Delta x$ ，因此不会被趋近于 $0$ ，其他的都可以忽略不计。

上面的是通用的求导方式，即：
$$f^{{}^{\prime }}(x)=\frac{\Delta f}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}$$
现在我们来试求 $y=\sin x$ 的导数。

你可以试着用代数方法求，我们这里试着用几何方法。

先看下面的图：

关注 $\sin$ 和 $\cos$ 的部分。

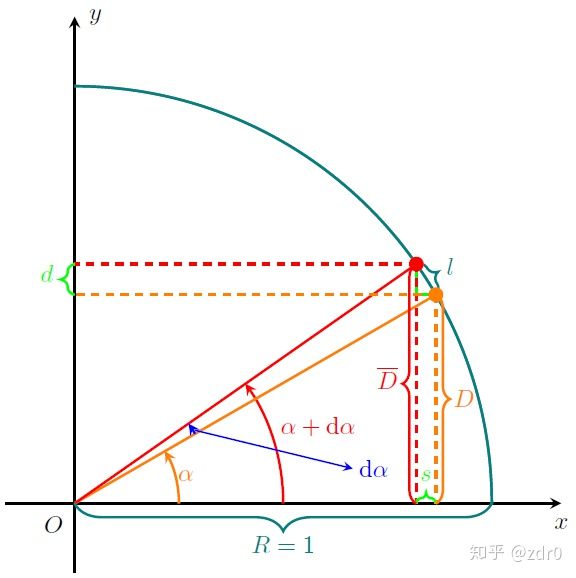
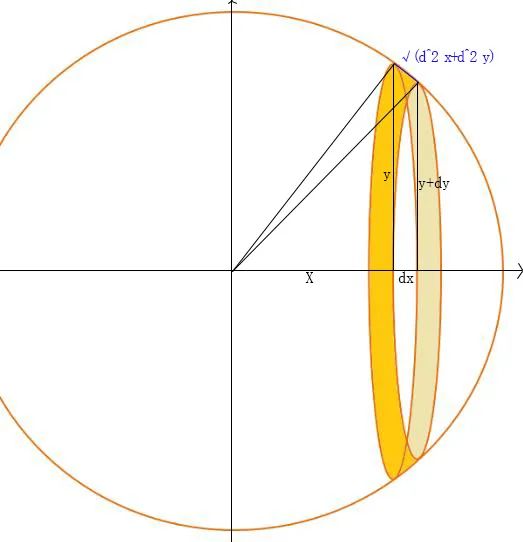
现在我们来看下面的一个单位圆：

单位圆的半径为 $r=1$ 。所以，竖直的橙色虚线的长度是 $\sin \alpha .$
竖直的红色虚线的长度是 $\sin (\alpha +\Delta \alpha ).$

因此 $d=\overline{D}-D=\sin (\alpha +\Delta \alpha )-\sin \alpha .$

现在我们把单位圆放大：

可以看见，我们把弧长放的越大，那么他就越接近一条直线。

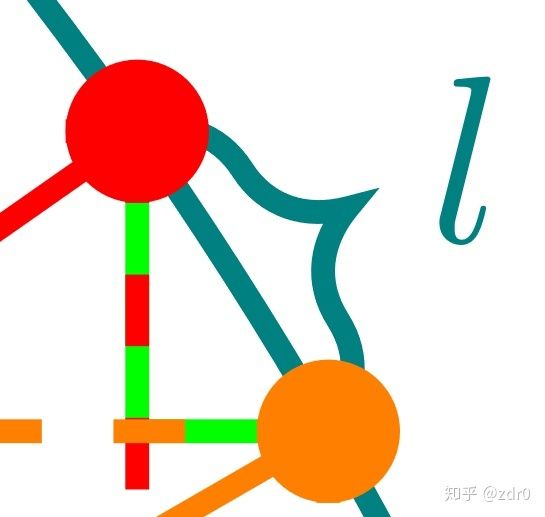
现在连接红点和橙点，如下图所示：

图片3中的青线是圆的一条 割线 ，可以想象，当红色点 充分接近 橙色点时（即转动的角度 $\Delta \alpha$ 充分小时），这条青色的割线将趋近于橙色点处的圆的 切线 。而我们知道， 连结圆心与切点的半径是垂直于切线的 （垂径定理）。所以，在转动的角度 $\Delta \alpha$ 充分小时，可近似认为图片1中的橙色实线半径 垂直于 这条青色的割线。不仅如此，在转动的角度充分小时，这这条青色的割线还近似于 弧 $l$ 。

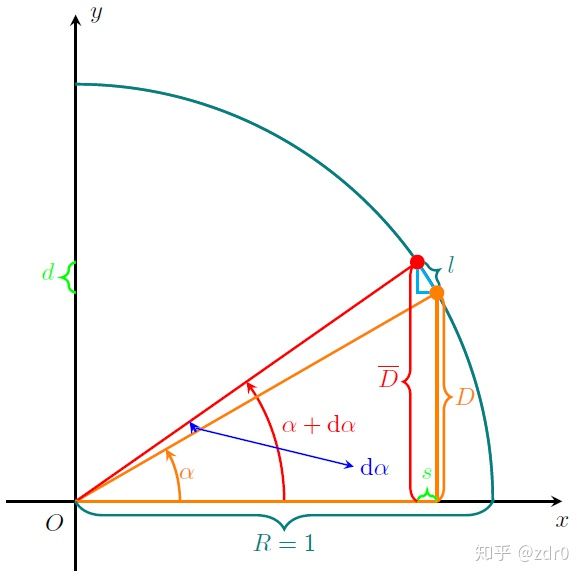
那么就会出现两个相似三角形，我将它们分别用橙色和青色进行重新进行标识，如下图所示：

则由相似性可知，图片4中的青色三角形在红色点处的角度是 $\alpha$ ：

则有 $d=\cos \alpha \cdot \Delta a.$

又 $\because d=\sin (\alpha +\Delta \alpha )-\sin \alpha$

$\therefore \frac{\Delta \sin \alpha }{\Delta \alpha }=\frac{\sin (\alpha +\Delta \alpha )-\sin \alpha }{\Delta \alpha }=\frac{\cos \alpha \cdot \Delta \alpha }{\Delta \alpha }=\cos \alpha$.

因此，${\sin }^{{}^{\prime }}x=\cos x.$

同理可得，
$${\cos }^{{}^{\prime }}x=-\sin x$$
$${\tan }^{{}^{\prime }}x=\frac{1}{{\cos }^{2}x}={\sec }^{2}x$$
$${\cot }^{{}^{\prime }}x=-\frac{1}{{\sin }^{2}x}=-{\csc }^{2}x$$
$${\sec }^{{}^{\prime }}x=\sec x\cdot \tan x$$
$${\csc }^{{}^{\prime }}x=-\csc x\cdot \cot x$$

1x03 微分（其三）——求导的几何意义：切线斜率

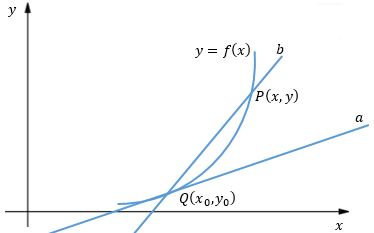
我们看一个函数 $f(x)$ 的图像。

现在，我们关注 $P,Q$ 两点。$a$ 是经过这两点的割线。现在，我们将 $P$ 越来越靠近 $Q$ ， $a$ 也逐渐下滑到 $b$ 的位置。我们说 $b$ 是函数 $y=f(x)$ 在 $Q$ 点处的切线。当然，也可以说是在 $(x_0,y_0)$ 处的切线。

你可能会说，我们为什么不把函数图像的切线直接定义成 经过且仅经过图像上一点的直线 呢？其实，很多函数的图像要么 不存在经过且仅经过图像上一点的直线 ，要么 存在很多条经过且仅经过图像上一点的直线 。而且，这样极限的定义还能够牵扯到一个重要的概念——导数。

其实，我们这条切线的方程可以表示为 $y=ax+b$ ，其中 $a$ 就是切线的斜率。通过第二节的证明，我们知道，当取的范围足够小（这里为 $PQ$ ），直线就越接近曲线的极限。此时，直线的斜率就是 竖轴增加的步长比上横轴增加的步长 ，也即 $\frac{\Delta y}{\Delta x}$ ，$y$ 的导数。

现在，我们就可以求出函数 $y=f(x)$ 在 $x_0$ 处的切线方程了。下面给出一个例子：

已知函数 $f(x)=x^2+5$ ，求出函数 $f(x)$ 的图像在 $x=-5$ 处的切线方程。

首先，我们求出 $f(x)$ 的导函数：
$$f^{{}^{\prime }}(x)=\frac{\Delta f}{\Delta x}=\frac{[(x+\Delta x{)}^2+5]-(x^2+5)}{\Delta x}=2x$$
当 $x=-5$ 时，$f^{{}^{\prime }}(-5)=-10$ .

所以 $x=-5$ 处的切线的方程为 $y=-10x+b$ ，现在我们要求出常数项。

将 $x=-5$ 带入原方程，得到 $y=50+b$ ，此时 $y=25$ ，因此 $25=50+b$ ，解得 $b=-25$ 。

所以，函数 $f(x)$ 的图像在 $x=-5$ 处的切线方程为 $y=-10x-25$ 。

同样也很容易得出，函数 $f(x)$ 的图像在 $x=x_0$ 处的切线方程为 $y=2x_{0}x-x_0^2$ .

1x04 微分（其四）——导数的计算法则，加法、乘法&链式法则

导数的加法法则为：
$$(f(x)+g(x){)}^{{}^{\prime }}=f^{{}^{\prime }}(x)+g^{{}^{\prime }}(x)$$
这灰常的显而易见：
$$(f(x)+g(x){)}^{{}^{\prime }}=\frac{\Delta f+\Delta g}{\Delta x}=\frac{\Delta f}{\Delta x}+\frac{\Delta g}{\Delta x}=f^{{}^{\prime }}(x)+g^{{}^{\prime }}(x)$$
（不要怕对无穷小量进行运算，之后会讲到什么时候不适合直接计算 洛不达，洛必错 ）

比如说，$(x^2+3x{)}^{{}^{\prime }}=(x^2{)}^{{}^{\prime }}+3x^{{}^{\prime }}=2x+3$.

导数的乘法法则为：
$$(f(x)\cdot g(x){)}^{{}^{\prime }}=f^{{}^{\prime }}(x)\cdot g(x)+f(x)\cdot g^{{}^{\prime }}(x)$$
证明如下：
$$\Delta (fg)=f(x+\Delta x)\cdot g(x+\Delta x)-f(x)\cdot g(x)$$
我们都知道，$ab-cd=b(a-c)+c(b-d)$.
$$=[f(x+\Delta x)-f(x)]\cdot g(x+\Delta x)+f(x)\cdot [g(x+\Delta x)-g(x)]$$
$$=\Delta f\cdot g(x+\Delta x)+f(x)\cdot \Delta g$$
两边同时除以 $\Delta x$ ：
$$\frac{\Delta (fg)}{\Delta x}=\frac{\Delta f}{\Delta x}\cdot g(x+\Delta x)+f(x)\cdot \frac{\Delta g}{\Delta x}$$
$$\because \Delta x\to 0.$$
$$\therefore g(x+\Delta x)\to 0.$$
$$\therefore (f(x)\cdot g(x){)}^{{}^{\prime }}=\frac{\Delta (fg)}{\Delta x}=f^{{}^{\prime }}(x)\cdot g(x)+f(x)\cdot g^{{}^{\prime }}(x).$$
证明完毕，我们来看一个例子：

已知
$$f(x)=\sin x\cdot \cos x$$
求 $f^{{}^{\prime }}(x)$ .

首先，根据乘法法则，我们知道
$$f^{{}^{\prime }}(x)={\sin }^{{}^{\prime }}x\cdot \cos x+\sin x\cdot {\cos }^{{}^{\prime }}x$$
又因为
$${\sin }^{{}^{\prime }}x=\cos x,{\cos }^{{}^{\prime }}x=-\sin x$$
所以
$$f^{{}^{\prime }}(x)={\cos }^{2}x-{\sin }^{2}x.$$
导数的链式法则为：
$$g(f(x){)}^{{}^{\prime }}=g^{{}^{\prime }}(f(x))\cdot f^{{}^{\prime }}(x)$$
具体的证明这里不细讲，详细的请见 这条知乎 。

下面列出更多的一些计算法则：

除法法则：
$${\left(\frac{f(x)}{g(x)}\right)}^{{}^{\prime }}=\frac{f^{{}^{\prime }}(x)g(x)-f(x)g^{{}^{\prime }}(x)}{g^2(x)}$$
反函数法则：
$${f^{-}}^{{}^{\prime }}(x)=\frac{1}{f^{{}^{\prime }}(x)}$$

1x05 微分（其五）——指数、对数&反三角函数の导数

我们现在来求一下指数函数 $y=a^x$ 的导数。

首先，我们求下极限：
$$y^{{}^{\prime }}=\underset{\Delta x\to 0}{\lim }\frac{a^{x+\Delta x}-a^x}{\Delta x}$$
$$=\underset{\Delta x\to 0}{\lim }{a}^x\frac{a^{\Delta x}-1}{\Delta x}$$
现在，我们进行换元： $z=a^x-1$.
$$y^{{}^{\prime }}=a^x\underset{z\to 0}{\lim }\frac{z}{{\log }_a(z+1)}$$
$$=a^x\underset{z\to 0}{\lim }\frac{1}{{\log }_a(z+1{)}^{\frac{1}{z}}}$$

现在我们求极限 ${\lim }_{x\to 0}\frac{1}{{\log }_a(x+1{)}^{\frac{1}{x}}}$ .

$$\underset{z\to 0}{\lim }\frac{1}{{\log }_a(z+1{)}^{\frac{1}{z}}}=\underset{x\to 0}{\lim }{e}^{\ln (x+1{)}^{\frac{1}{x}}}$$
$$=e^{{\lim }_{x\to 0}\frac{\ln (x+1)}{x}}$$
$$=e^{{\lim }_{x\to 0}\frac{\frac{1}{x+1}}{1}}$$
$$=e^1$$
$$=e$$
具体细节我们之后再来讲。那指数函数的导数就可以简化表示：
$$y^{{}^{\prime }}=a^x\frac{1}{{\log }_{a}e}$$
$$=a^x\frac{1}{\frac{\ln e}{\ln a}}$$
$$=a^x\ln a.$$
因此，${a^x}^{{}^{\prime }}=a^x\ln a.$

对数函数 $y={\log }_{a}x$ 是指数函数 $y=a^x$ 的反函数，因此：
$$({\log }_{a}x{)}^{{}^{\prime }}=\frac{1}{{a^x}^{{}^{\prime }}}=\frac{1}{a^x\ln a}.$$
你也可以试着推导一下反三角函数的导数公式，下面仅列出 $\arcsin x$ 的求导过程：
$${\arcsin }^{{}^{\prime }}x=\frac{1}{{\sin }^{{}^{\prime }}y}$$
$$=\frac{1}{\cos y}$$
由诱导公式得：
$$=\frac{1}{\sqrt{1-{\sin }^{2}y}}$$
$$=\frac{1}{\sqrt{1-{\sin }^2\arcsin x}}$$
$$=\frac{1}{\sqrt{1-x^2}}$$
所有反三角函数的导数如下表：
$${\arcsin }^{{}^{\prime }}x=\frac{1}{\sqrt{1-x^2}}$$
$${\arccos }^{{}^{\prime }}x=-\frac{1}{\sqrt{1-x^2}}$$
$${\arctan }^{{}^{\prime }}x=\frac{1}{1+x^2}$$
$${\text{arccot}}^{{}^{\prime }}x=-\frac{1}{1+x^2}$$
$${\text{arcsec}}^{{}^{\prime }}x=\frac{1}{|x|\sqrt{x^2-1}}$$
$${\text{arccsc}}^{{}^{\prime }}x=-\frac{1}{|x|\sqrt{x^2-1}}$$
博主博主，你后面三个反函数是怎么打出来的啊

直接用 \text{} 就好了啊

1x06 微分（六）——洛必达法则&应用

在我们求 $y=a^x$ 的导数的时候，我们用到了洛必达法则，因此有必要说一下。

洛必达法则如下：
$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f^{{}^{\prime }}(x)}{g^{{}^{\prime }}(x)}$$
其中 $f(x)$ 和 $g(x)$ 要满足如下条件：

$(1)$
$$\underset{x\to a}{\lim }f(x)=0/\infty$$
$$\underset{x\to a}{\lim }g(x)=0/\infty$$
$(2)$
在 $a$ 的去心邻域（去心邻域是啥？回到 1x01 看看）内，两者皆可导，且 $g^{{}^{\prime }}(x)\ne 0$.

$(3)$
$$\underset{x\to a}{\lim }\frac{f^{{}^{\prime }}(x)}{g^{{}^{\prime }}(x)}=A(A\in (\mathbb{R}\cup \pm \infty ))$$

下面我们来证明一下： （用到了柯西中值定理，可以自己去查一下）

由于函数在 $a$ 点的 去心邻域可导 ，也就是说函数在这个 $a$ 的去心邻域内 连续 。那么我们套用 柯西中值定理 ，在 $x$ 趋向于 $a$ 时，可以得到在区间 $(a,x)$ 内找到一个点 $\xi$ ，使得：
$$\frac{f(x)-f(\xi )}{g(x)-g(\xi )}=\frac{f^{{}^{\prime }}(\xi )}{g^{{}^{\prime }}(\xi )}$$
我们将这两个函数做差可得：
$$\underset{x\to a}{\lim }\frac{f(x)-f(a)}{g(x)-g(a)}-\frac{f(x)}{g(x)}$$
$$=\underset{x\to a}{\lim }f(x)g(a)-f(a)g(x)=0$$
$$\therefore \frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f^{{}^{\prime }}(\xi )}{g^{{}^{\prime }}(\xi )}=\frac{f(x)}{g(x)}$$
因为 $x$ 趋近于 $a$ 时， $\xi$ 也趋近于 $a$ ，因此：
$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a}{\lim }\frac{f^{{}^{\prime }}(x)}{g^{{}^{\prime }}(x)}$$
得证。

现在我们来运用一下洛必达法则，计算 $\frac{\sin x}{x}$ 在 $x\to 0$ 时的极限。

运用洛必达法则：
$$\underset{x\to 0}{\lim }\frac{\sin x}{x}=\underset{x\to 0}{\lim }\frac{{\sin }^{{}^{\prime }}x}{x^{{}^{\prime }}}=\underset{x\to 0}{\lim }\cos x=1$$
因此
$$\underset{x\to 0}{\lim }\frac{\sin x}{x}=1.$$
我们将在 $x\to 0$ 时， $\sin x$ 和 $x$ 称为等价无穷小，记作 $\sin x\sim x$ 。

2x01 积分（一）——积分的定义&牛顿—莱布尼茨公式

我们还是从小汽车的例子开始，只不过这一次我们知道了 $v$ 和 $t$ 的关系，要求 $s$ 与 $t$ 的关系。我们将 $s$ 称为 $v$ 对 $t$ 的积分，简称为 $v$ 的积分，记作：
$$\int vdt=s$$
这里的 $dt$ 和 $\Delta t$ 是一个意思。

我们通常将 $f(x)$ 的积分称为 $f(x)$ 的原函数，记作 $F(x)$ 。

显而易见的是，积分和微分互为逆运算，即：
$$\int f^{{}^{\prime }}(x)dx=f(x)$$
哒卡，上面的式子是错误的！因为在进行微分的过程中我们消掉了常数项，因此我们需要再把常数项加上，即：
$$\int f^{{}^{\prime }}(x)dx=f(x)+C$$

• 大概很多人分不清 微分和求导的区别 。求导出来的是 一个函数 ，比如 $x^2$ 的导数是 $2x$ 。但是微分求出来是一个 无穷小量 （原谅我用了这个词），比如 $x^2$ 的微分是 $2dx$ 。我们称微分后 $dx$ 的次数相等的函数称为等价无穷小函数，例如 $\sin x$ 的微分为 $dx\cos x$ ， $x$ 的微分为 $dx$ ，因为两者都有一个 $dx$ ，因此它们两个是等价无穷小函数。

• 而关于为什么 $\int$ 后面有个 $dx$ ，是因为 积分是 微分 的逆运算 ，因此需要在后面加上 微分算子 ，求出来才是一个函数，而非什么奇怪的无穷量。

既然如此，我们可以很容易就得出以下积分公式：
$$\int Cdx=Cx+C_1$$
$$\int x^{a}dx=\frac{x^{a+1}}{a+1}+C$$
$$\int \frac{1}{x}dx=\ln |x|+C$$
$$\int a^{x}dx=\frac{a^x}{\ln x}+C$$
$$\int \sin xdx=-\cos x+C$$
$$\int \cos xdx=\sin x+C$$
…

更多的积分公式详见 这条知乎 。

现在，我们要求当 $v=2t$ 时，小车在第 $5$ 秒到第 $10$ 秒走过的路程。怎么求呢？这时候我们就要用到大名鼎鼎的 牛顿—莱布尼茨公式 。

牛顿—莱布尼茨公式如下：
$${\int }_a^{b}f(x)dx=F(b)-F(a)=F(x){|}_a^b$$
其中
$${\int }_a^{b}f(x)dx$$
表示函数 $f(x)$ 在区间 $[a,b]$ 内的定积分，在这里对应 $[a,b]$ 秒所行过的路程，等价于 $F(x){|}_a^b$ 。因为：
$$s=\int vdt=t^2$$
因此小车在第 $5$ 秒到第 $10$ 秒走过的路程为
$$s{|}_5^{10}=10^2-5^2=75$$
这就是定积分的计算方式。

2x02 积分（二）——积分的几何意义&积分法则

如下图所示：

我们说函数 $f(x)$ 与 $x$ 轴在 $[a,b]$ 这个区间内围成的面积为
$${\int }_a^{b}f(x)dx$$
为什么呢？

我们知道，要想求出曲边梯形 $x=a$ 、 $x=b$ ， $f(x)$ 和 $x$ 轴所围成面积，首先对曲边梯形均等分割成 $n$ 个曲边梯形，如图：

当 $n$ 足够大时，每个小曲边梯形就近似于矩形，即每个小曲边梯形的面积可以用矩形的面积来近似。

因此，令每个小长方形的面积为 $s_i$ ，则
$$S=\sum _{i=1}^n{s}_i$$
$$=f(a)\Delta x+f(a+\Delta x)\Delta x+f(a+2\Delta x)\Delta x+...+f(a+(n-1)\Delta x)\Delta x$$
$$=\sum _{j=0}^{n-1}f(a+j\Delta x)\Delta x$$
$$\because \underset{\Delta x\to 0}{\lim },n\to \infty$$
$$\therefore \underset{\Delta x\to 0}{\lim }\sum _{j=0}^{n-1}f(a+j\Delta x)\Delta x=\underset{\Delta x\to 0}{\lim }[F(a+n\Delta x)-F(a)]=F(b)-F(a)$$
$$\because F(b)-F(a)=F(x){|}_a^b={\int }_a^{b}f(x)dx$$
$$\therefore S={\int }_a^{b}f(x)dx$$
详细的证明可以看 这条知乎 。 反正我看不懂

积分的加法法则如下：
$$\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx$$
非常的显然，将两个面积叠加起来不就是它们面积的和嘛。

顺带一提，我们通常用 $u$ 和 $v$ 来代替函数。那么，积分的加法法则就可以表示成：
$$\int (u+v)dx=\int udx+\int vdx$$
积分的数乘法则如下：
$$\int Cf(x)dx=C\int f(x)dx$$
这和加法法则是对应的。

很遗憾的是，积分并没有乘法法则和链式法则。我们继续往下看。

积分的分部积分法是指：
$$\int (uv)dx=u\int vdx-\int u^{{}^{\prime }}(\int vdx)dx$$
也可以写作：
$$\int (uv)dx=uV-\int u^{{}^{\prime }}Vdx$$
这是怎么来的？

分部积分法是基于 导数的乘法法则 ：
$$(uv{)}^{{}^{\prime }}=u{v}^{{}^{\prime }}+u^{{}^{\prime }}v$$
求每边的积分，然后重排：
$$\int (uv{)}^{{}^{\prime }}dx=\int (u{v}^{{}^{\prime }})dx+\int (u^{{}^{\prime }}v)dx$$
$$uv=\int (u{v}^{{}^{\prime }})dx+\int (u^{{}^{\prime }}v)$$
$$\int (u{v}^{{}^{\prime }})dx=uv-\int (u^{{}^{\prime }}v)dx$$
再对 $v$ 求积分：
$$\int (uv)dx=u\int vdx-\int u^{{}^{\prime }}(\int vdx)dx$$
也可以写作：
$$\int (uv)dx=uV-\int u^{{}^{\prime }}Vdx$$
我们来看一个例子：
求
$$\int x\cos xdx$$
令 $u=x$ ， $v=\cos x$ ：
$$u^{{}^{\prime }}=x^{{}^{\prime }}=1,\int vdx=\int \cos xdx=\sin x$$
$$\therefore \int x\cos xdx=x\sin x-\int \sin xdx$$
$$=x\sin x+\cos x+C$$
再来看一个例子：求
$$\int \ln xdx$$
只有一个函数，我们就令 $v=1$ ，求得：
$$\int \ln xdx=x\ln x-\int x\cdot \frac{1}{x}dx=x\ln x-x+C$$
换元积分法是指将一个函数换元之后简化原式的一种求法。例如：
$$\int f(g(x))g^{{}^{\prime }}(x)dx=\int f(u)du$$
接着我们可以求 $f(u)$ 的积分，然后把 $g(x)$ 代回去 $u$ 里。

像这样：
求
$$\int 2x\cos x^{2}dx$$
因为 ${x^2}^{{}^{\prime }}=2x$ ，因此我们可以使用换元法：
$$\int \cos udu$$
求积分得：
$$\int \cos udu=\sin u+C$$
再将 $u=x^2$ 带入得：
$$\int 2x\cos x^{2}dx=\sin x^2+C$$
我们再来看一个比较复杂的例子：
求
$$\int \frac{x}{x^2+1}dx$$
因为 $(x^2+1{)}^{{}^{\prime }}=2x$ ，因此我们需要重排一下式子：
$$\frac{1}{2}\int \frac{2x}{x^2+1}dx$$
令 $u=x^2+1$ ，得：
$$\frac{1}{2}\int \frac{1}{u}du=\frac{1}{2}\ln u+C$$
将 $u=x^2+1$ 带入上式得：
$$\int \frac{x}{x^2+1}dx=\frac{1}{2}\ln (x^2+1)+C$$

2x03 积分（三）——柯西主值&Gamma函数

想象一个函数 $f(x)=\frac{1}{\ln x}$ 。这个函数有一个无穷点 $x=1$ ，我们称为 奇点 。

（If you can）

它的积分
$${\int }_0^t\frac{1}{\ln x}dx$$
通常记作 $\text{li}t$ 。

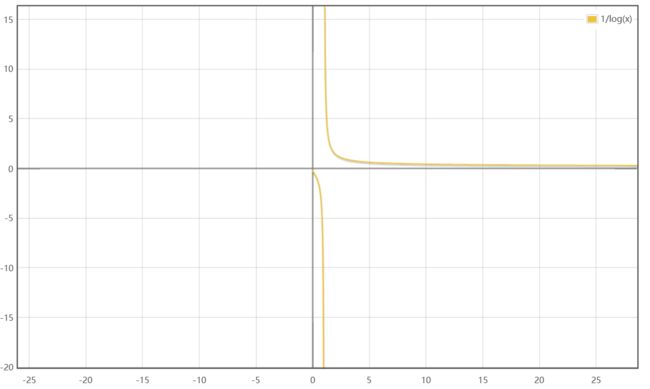
等等等等，当 $x=1$ 时，函数值不存在，那怎么能积分呢？我们先来看看它的图像：

更离谱了，函数不仅不连续，还有 $2$ 个无穷点， $1$ 个断点。

因此，我们要使用 柯西主值 来定义它。柯西主值是在微积分中，实数线上的某类 瑕积分 ，为纪念柯西而得此名。

相信你已经糊涂了。瑕积分是啥？

瑕积分，就是对于一个函数，在存在 奇点 的区间内进行积分。为了过滤掉这个奇点，我们要使得一个无穷小量 $\delta \to 0^{+}$ （ $0^{+}$ 的意思是从大于 $0$ 的位置趋近），使其能够表示 奇点附近的去心邻域 。（又提到了去心邻域）

我们假设这个奇点是 $c$ ，我们可得：
$${\int }_a^{b}f(x)dx=\underset{\delta \to 0^{+}}{\lim }\left({\int }_a^{c-\delta }f(x)dx+{\int }_{c+\delta }^{b}f(x)dx\right)$$
锵锵，我们这样就把 $c$ 这个点去掉啦！

如果有多个奇点，我们也可以类似操作，只不过要分成更多的部分。

现在，我们就可以定义 $\text{li}t$ 了：
$$\text{li}t=\underset{\delta \to 0^{+}}{\lim }\left({\int }_0^{1-\delta }\frac{1}{\ln x}dx+{\int }_{1+\delta }^t\frac{1}{\ln x}dx\right)$$

由于这个积分在 $x$ 趋近于 $0$ 时，值会趋近于 $-\infty$ ，有些数学家为了避免麻烦，常会选择另外一个相似的定义， 欧拉对数积分定义为 ：
$$\text{Li}t=\text{li}t-\text{li}2$$
等价于
$$\text{Li}t={\int }_2^t\frac{1}{\ln x}dx$$
当 $x\to +\infty$ 时，函数的渐进表现如下：
$$\text{li}x=O(\frac{x}{\ln x})$$
（什么复杂度，竞赛生狂喜）

在数论中这个函数也十分重要。高斯素数定理指出：
$$\pi (x)\sim \text{li}x$$
我愿称之为我学数论以来见过的最精简、最美丽、最奇特的定理公式，将离散和连续联系了起来。

是不是很好奇 $\text{li}x$ 的积分？很遗憾，它并不能表示成基本函数的公式组合。它的积分如下：
$$\int \text{li}xdx=x\text{li}x-\text{Ei}(2\ln x)+C$$
其中 $\text{Ei}$ 是指数反积分函数，
$$\text{Ei}x={\int }_x^{\infty }\frac{e^{-t}}{t}dt$$
这一函数可用来计算无限片状分布声源的辐射噪声场。具体的一些概念涉及到了复变函数和泛函分析。除此以外还有 $\text{Si}$ 、 $\text{Ci}$ 等。详见 这里 。

它们有如下关系：
$$\text{Ei}\ln x=\text{Li}x$$
$\Gamma$ 函数的定义如下：
$$\Gamma (x)={\int }_0^{+\infty }{t}^{x-1}{e}^{-t}dt(x>0)$$
在复数域上伽玛函数定义为：
$$\Gamma (z)={\int }_0^{+\infty }{t}^{z-1}{e}^{-t}dt(\text{Re}(x)>0)$$
伽马函数还有一种定义（欧拉无穷乘积定义）：
$$\Gamma (z)=\frac{1}{z}\prod _{n=1}^{\infty }\left[{\left(1+\frac{z}{n}\right)}^{-1}{\left(1+\frac{1}{n}\right)}^z\right]$$
通过分部积分的方法，可以推导出这个函数有如下的递归性质：
$$\Gamma (x+1)=x\Gamma (x)$$
于是很容易证明，伽马函数可以当成是阶乘在实数集上的延拓。对于正整数n，具有如下性质：
$$\Gamma (n)=(n-1)!$$
对于 $x\in (0,1)$ ，有：
$$\Gamma (1-x)\cdot \Gamma (x)=\frac{\pi }{\sin \pi x}$$
这个公式被称为 余元公式 。

由此可以推出以下重要的概率公式：

$$\Gamma (\frac{1}{2})=\sqrt{\pi }$$

其对数的导数称为 Digamma 函数，即
$$\psi (x)=\ln \Gamma (x{)}^{{}^{\prime }}=\frac{{\Gamma }^{{}^{\prime }}(x)}{\Gamma (x)}$$
Digamma 函数又与调和级数相关，即
$$\psi (n+1)=H_n+\gamma$$
其中 $\gamma$ 是欧拉常数。

而对于任意 $x$ 有：
$$\psi (x+1)=\psi (x)+\frac{1}{x}$$
黎曼 $\zeta$ 函数也与其紧密相关。 $\zeta$ 函数的定义如下：
$$\zeta (s)=\sum _{n=1}^{\infty }{n}^{-s}$$

2x04 积分（四）——含 $2a+b$ 的积分公式推导（可跳过）

一、求
$$\int \frac{1}{ax+b}dx$$
令 $t=ax+b$ ，则 $dt=adx$ 。
$$\therefore dx=\frac{1}{a}dt$$
$$\therefore \int \frac{1}{ax+b}dx=\frac{1}{a}\int \frac{1}{t}dt=\frac{1}{a}\cdot \ln |t|+C$$
将 $t=ax+b$ 带入上式得：
$$\int \frac{1}{ax+b}=\frac{1}{a}\cdot \ln |ax+b|+C$$
二、求
$$\int (ax+b{)}^{\mu }dx$$
令 $t=ax+b$ ，则 $dt=adx$ 。
$$\therefore dx=\frac{1}{a}dt$$
$$\therefore \int (ax+b{)}^{\mu }dx=\frac{1}{a}\int t^{\mu }dt=\frac{1}{a}\cdot \frac{t^{\mu +1}}{\mu +1}+C$$
将 $t=ax+b$ 代入上式得：
$$\int (ax+b{)}^{\mu }dx=\frac{1}{a}\cdot \frac{(ax+b{)}^{\mu +1}}{\mu +1}+C$$
三、求
$$\int \frac{x}{ax+b}dx$$
令 $t=ax+b$ ，则 $dt=adx$ 。
$$\therefore dx=\frac{1}{a}dt,x=\frac{1}{a}(t-b)$$
$$\therefore \int \frac{x}{ax+b}dx=\frac{1}{a^2}\int \left(1-\frac{b}{t}\right)dt$$
化简得
$$\frac{1}{a^2}\int \left(1-\frac{b}{t}\right)dt=\frac{1}{a^2}(t-b\cdot \ln |t|)+C$$
将 $t=ax+b$ 代入上式得：
$$\int \frac{x}{ax+b}dx=\frac{1}{a^2}(ax+b-b\cdot \ln |ax+b|)+C$$
四、求
$$\int \frac{1}{x(ax+b)}dx$$
设
$$\frac{1}{x(ax+b)}=\frac{A}{x}+\frac{B}{ax+b}$$
可得
$$\{\begin{array}{l}A=\frac{1}{b}\\ \\ B=-\frac{a}{b}\end{array}$$
因此
$$\int \frac{1}{x(ax+b)}dx=\int [\frac{1}{bx}-\frac{a}{b(ax+b)}]dx$$
$$=\frac{1}{b}\int \frac{1}{x}dx-\frac{a}{b}\int \frac{1}{ax+b}dx$$
$$=\frac{1}{b}\int \frac{1}{x}dx-\frac{1}{b}\int \frac{1}{ax+b}d(ax+b)$$
$$=\frac{1}{b}\cdot \ln |x|-\frac{1}{b}\cdot \ln |ax+b|+C$$
由对数的计算法则可得
= 1 b ⋅ ln ⁡ ∣ x a x + b ∣ + C =\dfrac 1b\cdot \ln\left|\dfrac{x}{ax+b}\right|+C =b1​⋅ln ​ax+bx​ ​+C
= − 1 b ⋅ ln ⁡ ∣ a x + b x ∣ + C =-\dfrac 1b\cdot \ln\left|\dfrac{ax+b}{x}\right|+C =−b1​⋅ln ​xax+b​ ​+C
更多公式如下：

1. $\int \frac{1}{ax+b}dx=\frac{1}{a}\cdot \ln |ax+b|+C$
2. $\int (ax+b{)}^{\mu }dx=\frac{1}{a}\cdot \frac{(ax+b{)}^{\mu +1}}{\mu +1}$
3. $\int \frac{x}{ax+b}dx=\frac{1}{a^2}(ax+b-b\cdot \ln |ax+b|)+C$
4. $\int \frac{x^2}{ax+b}dx=\frac{1}{a^3}\left[\frac{1}{2}(ax+b{)}^2-2b(ax+b)+b^2\cdot \ln |ax+b|\right]$
5. ∫ 1 x ( a x + b ) d x = − 1 b ⋅ ln ⁡ ∣ a x + b x ∣ + C \int\dfrac{1}{x(ax+b)}dx=-\dfrac 1b\cdot \ln\left|\dfrac{ax+b}{x}\right|+C ∫x(ax+b)1​dx=−b1​⋅ln ​xax+b​ ​+C
6. ∫ 1 x 2 ( a x + b ) d x = − 1 b x + a b 2 ⋅ ln ⁡ ∣ a x + b x ∣ + C \int\dfrac{1}{x^2(ax+b)}dx=-\dfrac 1{bx}+\dfrac{a}{b^2}\cdot \ln\left|\dfrac{ax+b}{x}\right|+C ∫x2(ax+b)1​dx=−bx1​+b2a​⋅ln ​xax+b​ ​+C
7. $\int \frac{x}{(ax+b{)}^2}dx=\frac{1}{a^2}\left(\ln |ax+b|+\frac{b}{ax+b}\right)+C$
8. $\int \frac{x^2}{(ax+b{)}^2}dx=\frac{1}{a^3}\left(ax+b-2b\cdot \ln |ax+b|-\frac{b^2}{ax+b}\right)+C$
9. ∫ 1 x ( a x + b ) 2 d x = 1 b ( a x + b ) − 1 b 2 ⋅ ln ⁡ ∣ a x + b x ∣ + C \int\dfrac{1}{x(ax+b)^2}dx=\dfrac{1}{b(ax+b)}-\dfrac{1}{b^2}\cdot \ln\left|\dfrac{ax+b}{x}\right|+C ∫x(ax+b)21​dx=b(ax+b)1​−b21​⋅ln ​xax+b​ ​+C

2x05 积分（五）——托里拆利小号&收敛的定义

托里拆利小号是一个旋转体，它由 $y=\frac{1}{x}(x\ge 1)$ 这个函数的图像旋转而来。图像如下：

神奇的一点是，它的体积是有限的，表面积却是无限的。我们来给出证明。

体积是面积的积分，我们只需要算出面积的函数 $s(x)$ ，对 $s$ 进行积分，则
$${\int }_1^{\infty }s(x)dx=V$$
而小号在平面 $x=x_0$ 上的横截面积为 $\pi {\left(\frac{1}{x_0}\right)}^2$ ，则我们可以得到：
$$V={\int }_1^{\infty }\pi {\left(\frac{1}{x}\right)}^{2}dx=\pi {\int }_1^{\infty }{\left(\frac{1}{x}\right)}^{2}dx=\pi \left[\underset{b\to \infty }{\lim }\left(-\frac{1}{b}\right)-\left(-\frac{1}{1}\right)\right]=\pi$$
故原积分收敛于 $1$ ，体积为 $\pi$ 。

而表面积是长度的积分，我们就要先求出小号在平面 $x=x_0$ 平面上的横截线长度。容易得出其为 $2\pi \frac{1}{x_0}$ 。则：
$$S={\int }_1^{\infty }2\pi \frac{1}{x_0}dx=2\pi \left(\underset{b\to \infty }{\lim }\ln |b|-\ln 1\right)$$
显然， ${\lim }_{b\to \infty }$ 时， $\ln b\to \infty$ ，因此原积分不收敛。

因此，托里拆利小号的体积为 $\pi$ ，而表面积无限。

我们定义，如果对于一个函数 $f(x)$ ，存在两个足够小的数 $\delta ,ϵ$ ，使其在 $x=x_0$ 时，$ϵ>|f(x_0+\delta )-f(x_0)|>0$ ，则称函数 $f(x)$ 在 $x_0$ 处收敛。

比如，托里拆利小号的体积便在 $x_0\to \infty$ 时，收敛至 $\pi$ ，而托里拆利小号的表面积不收敛。

2x06 积分（六）——圆锥和球的体积&证明

小学生都知道，圆锥的体积公式是 $V=\frac{1}{3}\pi r^{2}h$ ，我们来严格的证明一下。

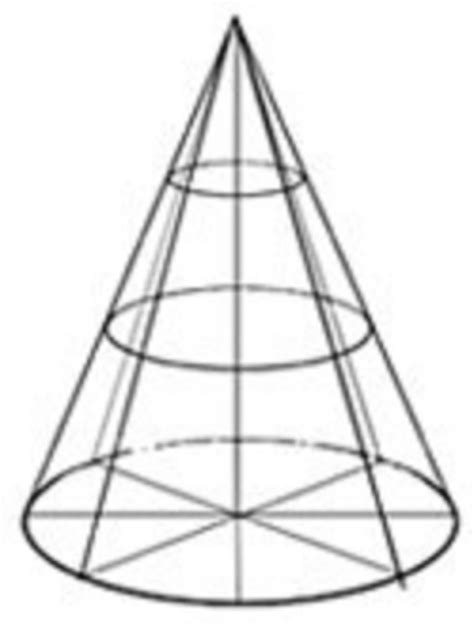
从上往下看，圆锥的截面半径是一个从 $0$ 到 $r$ 的正比例函数。

这个截面的斜边斜率恰为 $\frac{r}{h}$ 。因此，我们将圆锥在 $y=y_0$ 这个平面上的截面面积表示如下：
$$S=\pi {\left(\frac{r{y}_0}{h}\right)}^2$$
则体积为
$$V=\int Sdy=\frac{1}{3}\pi r^{2}h$$

我们现在来计算一下球的体积公式。

设球的半径为 $R$ ，
我们把球（我们通过半球来考虑）切成 $n$ 片，就是一个一个的圆，设圆的半径分别为 $r$ 。

面积为
$$S(r)=\pi r^{}$$