4、【逻辑回归】信用卡欺诈检测(下采样、SMOTE,调整sigmod函数阈值)
对于一个二分类问题,首先想到的还是逻辑回归!(我愿称逻辑回归为最nb的二分类算法,目前为止)
s i g m o d ( z ) = 1 1 + e − z 值 域 [ 0 , 1 ] sigmod(z)\ =\ {1\over{1+e^{-z}}} \\ 值域[0,1] sigmod(z) = 1+e−z1值域[0,1]
y ( i ) = Q T ∗ x i + E i y^{(i)}\ =\ Q^T*x^i\ +\ E^i y(i) = QT∗xi + Ei
- sigmod函数实则将数值转为概率值,一般z取QX
( θ 0 , θ 1 , θ 2 ) ∗ ( 1 , X 1 , X 2 ) . T = θ 0 + θ 1 X 1 + θ 2 X 2 h ( θ T X ) = g ( θ T X ) (\theta_0,\theta_1,\theta_2)\ *\ (1,X1,X2).T =\ \theta_0\ +\theta_1X_1\ +\ \theta_2X_2 \\ h(\theta^TX)\ =\ g(\theta^TX) (θ0,θ1,θ2) ∗ (1,X1,X2).T= θ0 +θ1X1 + θ2X2h(θTX) = g(θTX)
信用卡欺诈检测
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
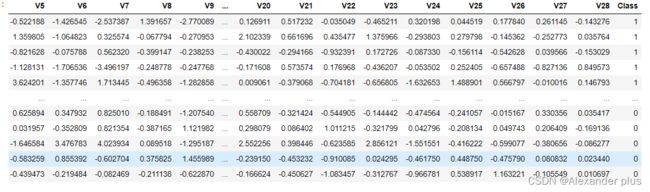
data = pd.read_csv('./creditcard.csv')
data.head()
对异常特征进行归一化处理
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
data.insert(0,'Norm_Amount',std.fit_transform(np.array(data['Amount']).reshape(-1,1)))
data = data.drop(['Amount','Time'],axis=1)
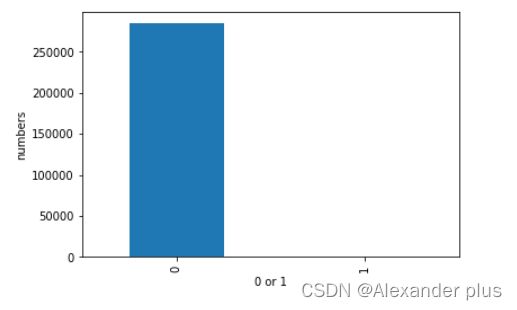
检测数据集正负样本分布情况
class_counts = pd.value_counts(values=data['Class'],sort=True).sort_index()
class_counts.plot(kind='bar')
plt.xlabel('0 or 1')
plt.ylabel('numbers')
- 此处样本数据极度不均衡,故考虑过采样或者下采样
- 下采样:从0里面随机挑取与1相同数目的样本
- 上采样:生成1的类别,使之与0类别相同或接近
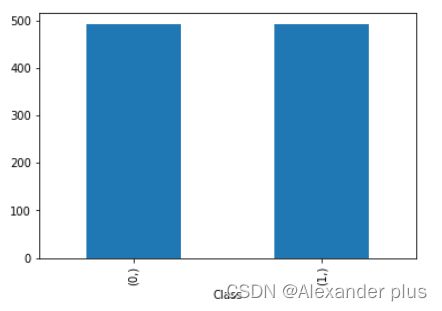
采用下采样调整数据正负不平衡
X = data.loc[:,data.columns != 'Class']
y = data.loc[:,data.columns == 'Class']
one_index = data[data.Class == 1].index
zero_index = data[data.Class == 0].index
random_zero_index = np.random.choice(zero_index,492,replace=False)
all_data_index_1 = np.concatenate([one_index,random_zero_index])
data_under = data.iloc[all_data_index_1,:]
data_under
X_under = data_under.loc[:,data_under.columns != 'Class']
Y_under = data_under.loc[:,data_under.columns == 'Class']
display(X_under,Y_under)
Y_under.value_counts().sort_index().plot(kind='bar')
Y_under.value_counts()
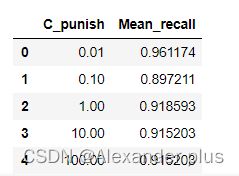
交叉验证并使用logic回归进行建模,确定最佳C
- 正则化惩罚项:避免过拟合
- 惩罚权重:例如,loss = loss + 1/2 * w^2 (lamuda * L2正则化,lambda代表惩罚力度)
- 确定最佳lambda值,使得模型recall最高
from sklearn.model_selection import train_test_split,cross_val_score,KFold
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,recall_score,classification_report
#对原始数据集进行切分(使用原始数据集中的test进行测试)
X_train,X_test,Y_train,Y_test = train_test_split(X,y,test_size=0.3,random_state=0)
#下采样数据集进行切分
X_under_train,X_under_test,Y_under_train,Y_under_test = train_test_split(X_under,Y_under,test_size=0.3,random_state=0)
def print_KFold_scores(x_train,y_train):
fold = KFold(5,shuffle=False)
C_punish = [0.01,0.1,1,10,100]#lambda
recall_tb = pd.DataFrame(columns=['C_punish','Mean_recall'])
recall_lst = []
for c in C_punish:
lr = LogisticRegression(penalty='l1',C=c)
lst = []
print("---------C为:",c)
for index,value in enumerate(fold.split(x_train)):
count = 1
lr.fit(x_train.iloc[value[0],:].values,y_train.iloc[value[0],:].values.ravel())
pred = lr.predict(x_train.iloc[value[1],:].values)
rs = recall_score(y_train.iloc[value[1],:].values,pred)
lst.append(rs)
print("test",count,"召回率为",rs)
count+=1
recall_lst.append(sum(lst)/len(lst))
recall_tb['Mean_recall'] = recall_lst
recall_tb['C_punish'] = C_punish
return recall_tb
bst_recall = print_KFold_scores(X_under_train,Y_under_train)
bst_recall
模型评估方法之混淆矩阵
import itertools
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
- 下采样样本进行预测
lr = LogisticRegression(C=0.01,penalty='l1')
lr.fit(X_under_train,Y_under_train)
y_pred = lr.predict(X_under_test)
conf = confusion_matrix(Y_under_test,y_pred)
plot_confusion_matrix(conf,[0,1])
- 我们可以看到,查全是比较好的,准确率(被误伤情况)也较好
将上述模型应用全部数据的测试集进行预测
lr = LogisticRegression(C=0.01,penalty='l1')
lr.fit(X_under_train,Y_under_train)
y_pred = lr.predict(X_test)
conf = confusion_matrix(Y_test,y_pred)
plot_confusion_matrix(conf,[0,1])
print("召回率",conf[1,1]/(conf[1,1]+conf[1,0]))
print("准确率",(conf[1,1]+conf[0,0])/(conf[1,1]+conf[0,1]+conf[1,0]+conf[0,0]))
- 召回率 0.9183673469387755
- 准确率 0.8816637992579849
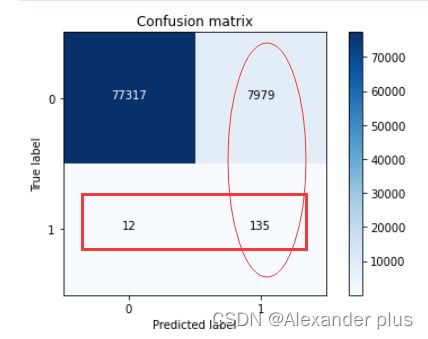
但是,如果一开始就拿全部数据进行建模,康康情况如何
lr = LogisticRegression()
lr.fit(X_train,Y_train)
y_pred = lr.predict(X_test)
conf = confusion_matrix(Y_test,y_pred)
plot_confusion_matrix(conf,[0,1])
print("召回率",conf[1,1]/(conf[1,1]+conf[1,0]))
print("准确率",(conf[1,1]+conf[0,0])/(conf[1,1]+conf[0,1]+conf[1,0]+conf[0,0]))
可以看到,直接拿原始数据进行建模预测,结果来看,查全率(recall),非常不理想,尽管准确率较高,但是我们试想,对于一个信贷检测的目的,尽可能找出有诈骗风险的用户更为重要,还是准确率更为重要呢?跟癌症检测同理,因此,在此处的测评指标中我们更倾向于recall这个指标。当然,不可否认,此处将无欺骗风险的客户识别为欺骗风险较高的客户在此处也是比较夸张了,实际生活中所需的维护代价过大,故笔者进一步探索,分别从调节sigmod的阈值(将0.5上调或者下调)以及向上采样)(SMOTE)进行模型完善。
通过调节sigmod函数的阈值进行查找最佳recall跟precision
lr = LogisticRegression(C=0.01,penalty='l1')
lr.fit(X_under_train,Y_under_train)
y_pred_undersample_proba = lr.predict_proba(X_under_test.values)
#此处将predict改为predict_proba,即传入sigmod中的概率值,以便调节sigmod阈值
#可能的阈值0-1
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
plt.figure(figsize=(10,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(Y_under_test,y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Threshold >= %s'%i)
Recall metric in the testing dataset: 1.0
Recall metric in the testing dataset: 1.0
Recall metric in the testing dataset: 1.0
Recall metric in the testing dataset: 0.9863945578231292
Recall metric in the testing dataset: 0.9251700680272109
Recall metric in the testing dataset: 0.8639455782312925
Recall metric in the testing dataset: 0.8299319727891157
Recall metric in the testing dataset: 0.7482993197278912
Recall metric in the testing dataset: 0.5850340136054422
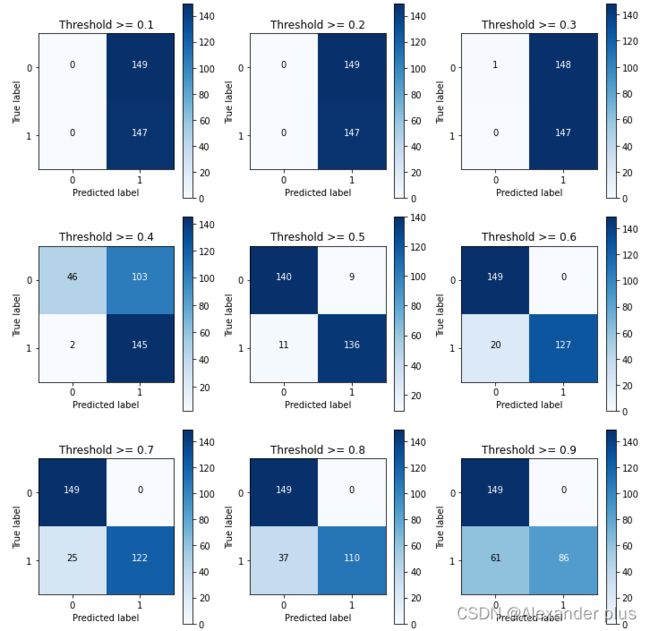
由此可见,0.4可能才是最佳阈值(上述测试仍在调整模型,故在under下采样数据集上进行调试)
使用SMOTE方法进行测试
import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
credit_cards=pd.read_csv('creditcard.csv')
columns=credit_cards.columns
features_columns=columns.delete(len(columns)-1)
features=credit_cards[features_columns]
labels=credit_cards['Class']
features_train, features_test, labels_train, labels_test = train_test_split(features,
labels,
test_size=0.3,
random_state=0)
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_resample(features_train,labels_train)
print(len(os_labels[os_labels==1]),len(os_labels[os_labels==0]))
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = print_KFold_scores(os_features,os_labels)
best_c
import numpy as np
lr = LogisticRegression(C = 0.10, penalty = 'l2')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()