- KANN 是一个独立的轻量级 C 语言库,用于构建和训练中小型人工神经网络,例如多层感知器、卷积神经网络和递归神经网络(包括 LSTM 和 GRU)。它实现了基于图的逆模自动微分,并允许构建具有递归等
一、软件介绍文末提供程序和源码下载KANN是一个独立的轻量级C语言库,用于构建和训练中小型人工神经网络,例如多层感知器、卷积神经网络和递归神经网络(包括LSTM和GRU)。它实现了基于图的逆模自动微分,并允许构建具有递归、共享权重和多个输入/输出/成本的拓扑复杂神经网络。与TensorFlow等主流深度学习框架相比,KANN的可扩展性较低,但它的灵活性接近,代码库要小得多,并且仅依赖于标准C库。与
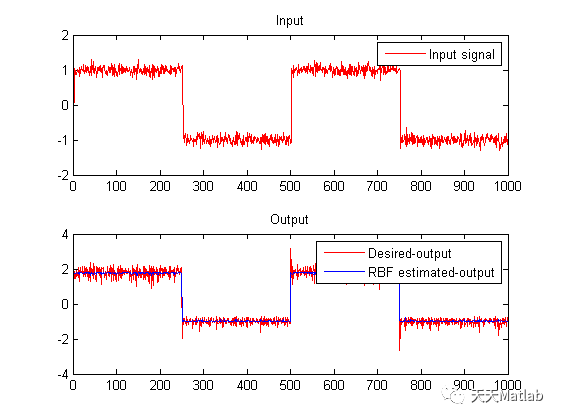
- 六自由度按摩机器人 MATLAB 仿真
本课题围绕六自由度(6-DOF)按摩机器人展开,旨在通过MATLAB仿真平台对其机械结构、运动学特性和控制策略进行建模与分析。六自由度机器人具备空间位置和姿态的全面调节能力,可实现复杂的按摩轨迹和多角度作用力控制。研究内容包括机器人正/逆运动学建模、轨迹规划(如五次多项式插值、笛卡尔路径)、动力学建模(使用Lagrange或Newton-Euler方法)以及基于PID或自适应控制算法的控制系统设计
- MATLAB软件二次开发:MATLAB面向对象编程
kkchenjj
仿真模拟matlab开发语言工业软件工业软件二次开发
MATLAB软件二次开发:MATLAB面向对象编程绪论面向对象编程的基本概念面向对象编程(Object-OrientedProgramming,OOP)是一种编程范式,它将程序设计围绕“对象”进行。在OOP中,对象是数据和可以对这些数据执行的操作的封装。每个对象都是一个特定类的实例,类定义了对象的属性(数据成员)和方法(函数)。OOP的三大特性包括:封装:将对象的属性和方法封装在一起,隐藏对象的内
- msk调制matlab代码,FSK,MSK,CPFSK调制与解调MATLAB仿真_通信工程.rar
羊男的迷宫
msk调制matlab代码
摘要:频移键控(FSK)是一种常见的数字调制,具有功率效率高及抗信道噪声性能良好的优势.本文探讨了频移键控的技术特性,包括多进制频移键控(MFSK),最小频移键控(MSK)和连续相位频移键控(CPFSK),还包括其相干解调及其蒙特卡洛误码率仿真.FSK利用载波的频率来传递信息,包络恒定,因此可以利用功率效率高的非线性放大器进行解调,它的优势在于对信道和硬件引起的幅度失真不敏感.另一方面,FSK频谱
- MATLAB代码实现了一个完整的ARIMA时间序列分析与预测流程
神经网络697344
算法深度学习MATLABmatlab信息可视化开发语言
%%1.数据准备years=(2010:2024)';data=[11894,12277,12777,13262,13902,14524,15037,15961,16724,...17767,19064,20056,20978,21676,22023]';%创建时间序列对象ts=timeseries(data,years,'Name','65岁以上人口');ts.TimeInfo.Units='y
- AttnRNN:参数更少,却断档碾压LSTM/GRU的新RNN
wq舞s
人工智能python深度学习deeplearningai科技pytorch
研究者与发布者为:CSDNwq舞s,知乎wqwsgithubwqws突破性进展!新型注意力RNN(AttnRNN)在长序列任务中全面超越传统RNN模型在深度学习领域,循环神经网络(RNN)及其变体GRU和LSTM长期以来一直是处理序列数据的首选架构。然而,它们在长序列任务中始终存在信息遗忘和梯度消失等问题。今天,我很高兴地宣布一种全新的RNN架构——AttnRNN,它在多个长序列基准测试中全面超越
- matlab实现MSK调制,单载波频域均衡,正交分解
feifeigo123
matlab开发语言
MSK调制,单载波频域均衡(SCFDE),正交分解MSK_FDE_ORTH/cpm.txt,424832MSK_FDE_ORTH/gen_tailsymbols_tab.m,943MSK_FDE_ORTH/gen_titled_trlls.m,1982MSK_FDE_ORTH/main_MSK_ORTH.m,11592MSK_FDE_ORTH/match_filter.asv,1026MSK_FD
- C语言教学大变革!DeepSeek如何改变高职院校编程课堂?
武汉唯众智创
c语言开发语言程序设计Deepseek
一、引言在当今数字化转型的浪潮中,程序设计与分析能力已成为高职教育中不可或缺的核心竞争力。作为编程语言的基础,C语言不仅训练学生的计算思维,还培养其算法实现能力。然而,当前高职院校的C语言教学面临诸多挑战,如实践环节薄弱、学生创新能力不足等。DeepSeek等新一代智能编码支持系统的出现,为这一现状带来了转机。该系统融合了深度神经网络与语义解析技术,能够智能生成代码、优化缺陷检测、解构程序逻辑,并
- matlab 欧拉角转四元数
点云侠
matlab与合成孔径雷达matlab开发语言算法
目录一、概述一、概述1、计算原理2、实现步骤3、主要函数三、代码实现四、结果展示一、概述目录一、概述一、概述1、计算原理2、实现步骤3、主要函数三、代码实现四、结果展示一、概述 将欧拉角转换为四元数是计算机图形学、机器人学和物理仿真中常见的任务。欧拉角通过一系列的角度描述物体在空间中的旋转,而四元数则提供了一种更加简洁和稳定的方式来实现旋转表示。设欧拉角为(α,β,γ)(\alpha,\beta
- matlab 渐进三角网(PTD)地面滤波(基础版)
点云侠
matlab点云工具箱matlab开发语言算法c++计算机视觉
目录一、算法原理1、PTD算法2、实现流程二、代码实现三、结果展示1、原始点云2、滤波结果代码是按照算法原理的复现,效率极低,只适合学习和理解算法。一、算法原理1、PTD算法 渐进三角网地面滤波算法(ProgressiveTINDensification,PTD)是一种广泛应用于机载LiDAR点云数据处理的滤波方法,旨在从复杂场景中精确分离地面点,以生成数字高程模型(DEM)。2、实现流程 P
- 脑机新手指南(二十)BCI2000 新手入门指南(下篇)
Brduino脑机接口技术答疑
脑机新手指南人工智能算法大数据
一、引言在上篇文章中,我们介绍了BCI2000的基本概念、特点和优势,以及安装、配置和基本使用流程。在本篇文章中,我们将深入探讨BCI2000的信号处理和分类算法,并提供一些实操的代码教程,帮助新手更好地掌握BCI2000的使用方法。二、BCI2000的信号处理(一)信号处理的基本概念在脑机接口系统中,信号处理是一个非常重要的环节,它的主要目的是从原始的脑电信号中提取有用的信息,并去除噪声和干扰。
- matlab有限元相场算法
bubiyoushang888
算法matlab机器学习
研究的目的是证明一种有限元相场算法,其中相场方程是完全耦合并同时求解的。不过,在这种情况下,完全耦合的方程是弹性和非守恒的阶参数;然而,该方法可作为其他相场模型完全耦合公式的模板。这是求解具有弹性不均匀性的Allen-Cohn方程的主要程序。有限元算法。该算法解决了非保守阶参数的演化问题。全耦合模式下应力列场的演化。取决于代码中Isolve参数的选择:对于Isolve-1,代码以长手格式和非优化模
- 什么是神经网络和机器学习?【云驻共创】
一键难忘
人工智能机器学习深度学习神经网络网络
什么是神经网络和机器学习?一.背景在当今数字化浪潮中,神经网络和机器学习已成为科技领域的中流砥柱。它们作为人工智能的支柱,推动了自动化、智能化和数据驱动决策的进步。然而,对于初学者和专业人士来说,理解神经网络和机器学习的本质是至关重要的。在本文中,我们将深入探讨这两个概念的内涵、工作原理以及彼此之间的联系。二.神经网络和机器学习简介神经网络和机器学习都是人工智能领域中的重要概念,它们通常用于解决各
- Github 2024-11-01 开源项目月报 Top19
老孙正经胡说
github开源Github趋势分析开源项目PythonGolang
根据GithubTrendings的统计,本月(2024-11-01统计)共有19个项目上榜。根据开发语言中项目的数量,汇总情况如下:开发语言项目数量Python项目9TypeScript项目3JavaScript项目3Svelte项目1JupyterNotebook项目1Ruby项目1HTML项目1Rust项目1Java项目1C++项目1Go项目1Python中的算法实现集合创建周期:2831天
- 贝叶斯网络与深度学习的结合:图像识别和分类
AI天才研究院
AI人工智能与大数据计算AI大模型企业级应用开发实战自然语言处理人工智能语言模型编程实践开发语言架构设计
本文我将为您撰写一篇关于"贝叶斯网络与深度学习的结合:图像识别和分类"的技术博客文章。这篇文章将深入探讨贝叶斯网络和深度学习在图像识别和分类领域的结合应用。我会遵循您提供的要求和结构模板,确保文章内容全面、深入且易于理解。让我们开始吧。贝叶斯网络与深度学习的结合:图像识别和分类关键词:贝叶斯网络、深度学习、图像识别、图像分类、概率推理、卷积神经网络、不确定性建模文章目录贝叶斯网络与深度学习的结合:
- c++基于BP神经网络的手写数字识别
鱼弦
机器学习设计类系统开发语言人工智能
鱼弦:CSDN内容合伙人、CSDN新星导师、全栈领域创作新星创作者、51CTO(Top红人+专家博主)、github开源爱好者(go-zero源码二次开发、游戏后端架构https://github.com/Peakchen)基于BP(Backpropagation)神经网络的手写数字识别是一种常见的机器学习应用。下面我将为您提供原理的详细解释、使用场景的解释以及一些相关的文献材料链接。原理详细解释
- pytorch底层原理学习--Libtorch
libtorchlibtorch是PyTorch的C++实现版本,可以认为所有的pytorch底层都是由c++实现,而pytorch的所有C++实现就叫libtorch,也就是我们在pytorch官网getstart页面下载的c++pytorch版本。我们用python写的pytorch神经网络代码都会通过pybind11将python转换为libtorch的C++代码。[官方文档](PyTorc
- LFM信号脉冲压缩时的关键问题仿真
kaikaile1995
matlab
matlab程序对雷达常用的线性调频信号(lfm信号)进行脉冲压缩时的关键问题进行了仿真,其中包括旁瓣抑制影响(加窗与不加窗)、多卜勒频移影响,并对时域脉压与频域脉压结果进行了对比分析,供相关技术人员参考。hanming.m对LFM信号时域加窗(海明窗)与未加窗进行了对比。duobule.m对LFM信号在不同多卜勒频移状况下进行了对比。lfm_pc.m对LFM信号时域脉压与频域脉压结果进行了对比。
- 基于MATLAB代码DWA算法的移动车路径规划
985计算机硕士
路径规划matlab算法android
基于MATLAB代码DWA算法的移动车路径规划,可实现动态避障和静态避障文章目录DWA(DynamicWindowApproach)是一种常用于移动机器人路径规划的局部路径规划算法。它通过在速度空间中采样,结合机器人的运动学约束和环境信息,选择最优的速度组合来实现避障和目标点导航。以下是一个基于DWA算法的MATLAB代码示例,用于实现移动车的路径规划:%DWA(DynamicWindowAppr
- Keras环境复现代码(三)
yanyiche_
keras深度学习人工智能
DQN雅达利Breakout强化学习实验要求明确实验目的:学习和实现深度Q学习(DQN),这是一种结合了Q学习和深度神经网络的强化学习算法,用于解决复杂的决策问题。清楚实验原理:1、深度Q学习(DeepQ-Network)将卷积神经网络与Q学习结合,解决高维视觉输入的强化学习问题:2、经验回放:将状态转换存储到缓冲区,打破数据相关性,稳定训练。3、目标网络:定期更新目标Q值计算网络,减少训练中的目
- Linux进程信号
xuanzdhc
C++linux运维服务器c++
目录概念信号种类信号生命周期信号的处理信号的清除概念进程信号是一种异步通信机制,用于进程间传递事件通知。它可以强制进程中断当前操作,转而执行预设的信号处理动作,是系统管理和进程控制的重要手段本质:信号是一个整数编号代表不同类型事件信号种类可靠信号保证传递(支持队列)可携带参数(通过siginfo_t结构体)需要显示设置sa_flags=SA_SIGINFO不可靠信号可能丢失(如短时间内多次发送同一
- 深度学习中常见激活函数总结
向左转, 向右走ˉ
深度学习人工智能pytorchpython
以下是一份深度学习激活函数的系统总结,涵盖定义、类型、作用、应用及选择影响,便于你快速掌握核心知识:一、激活函数的定义在神经网络中,激活函数(ActivationFunction)是神经元计算输出的非线性变换函数,作用于加权输入和偏置之和:输出=f(加权和+偏置)核心价值:引入非线性,使神经网络能够拟合任意复杂函数(无激活函数的深度网络等价于单层线性模型)。二、常见激活函数类型1.线性函数(Lin
- AI人工智能 神经网络
马里亚纳海沟网
人工智能神经网络深度学习笔记运维全文检索搜索引擎
**AI人工智能神经网络概述**神经网络是并行计算设备,它们试图构建大脑的计算机模型。背后的主要目标是开发一个系统来执行各种计算任务比传统系统更快。这些任务包括模式识别和分类,近似,优化和数据聚类什么是人工神经网络(ANN)人工神经网络(ANN)是一个高效的计算系统,其核心主题是借用生物神经网络的类比。人工神经网络也被称为人工神经系统,并行分布式处理系统和连接系统。ANN获取了大量以某种模式相互连
- educoder机器学习 --- 神经网络
木右加木
educoder机器学习神经网络
第1关:神经网络基本概念1、C第2关:激活函数#encoding=utf8defrelu(x):'''x:负无穷到正无穷的实数'''#*********Begin*********#ifx<=0:return0else:returnx#*********End*********#第3关:反向传播算法#encoding=utf8importosimportpandasaspdfromsklearn.
- 回归预测 | MATLAB实现LSTM-SVR(长短期记忆神经网络-支持向量机)多输入单输出
matlab科研社
神经网络回归matlab
✅作者简介:热爱数据处理、数学建模、仿真设计、论文复现、算法创新的Matlab仿真开发者。更多Matlab代码及仿真咨询内容点击主页:Matlab科研工作室个人信条:格物致知,期刊达人。内容介绍长短期记忆神经网络(LSTM)作为一种循环神经网络(RNN)的变体,擅长处理序列数据并捕捉长期依赖关系,而支持向量机(SVR)则是一种强大的回归算法,能够有效地处理高维数据并防止过拟合。将两者结合的LSTM
- 服务器pci数据捕获和信号处理 感叹号,PCI数据捕获和信号处理控制器win7驱动
这是PCI数据捕获和信号处理控制器win7驱动下载,有些电脑在安装了系统后会在设备管理器中出现PCI数据捕获和信号处理控制器黄色感叹号提示,此时需要安装“IntelTurboBoost”驱动软件。软件介绍有时候我们装完系统的时候,各种驱动都安装完毕了,然后发现系统属性里面的设备管理器其他设备—PCI数据捕获和信号处理器控制器上还是有个问号,此款驱动就是解决这个问题的。PCI数据捕获和信号处理控制器
- 数字信号处理(DSP)全方位学习指南
本文还有配套的精品资源,点击获取简介:数字信号处理(DSP)是信息技术的关键部分,涉及多种数字信号的分析与处理技术,广泛应用于多个技术领域。本指南深入探索DSP的集成开发环境(IDE),基础概念,以及专业词汇,旨在帮助读者系统掌握DSP原理和实践技能。内容涵盖DSP集成开发环境CCS的使用、基础知识如傅里叶变换与滤波器设计,以及专业术语的学习。此外,还介绍了DSP在音频、图像处理和通信系统中的实际
- 大语言模型(LLM)笔记
笑衬人心。
大模型学习语言模型笔记人工智能
一、什么是大语言模型(LLM)?LLM(LargeLanguageModel)是基于Transformer架构构建,并在海量文本语料上训练出的具备自然语言理解和生成能力的深度神经网络模型。其本质任务是**预测下一个token(词/字/符号)**的概率分布,但通过大规模参数和数据的支持,表现出类人智能的行为。二、核心架构:Transformer由Google在2017年提出,是目前LLM的主流架构。
- Milvus向量数据库入门指南
longfei.li
milvus数据库人工智能
一、Milvus简介Milvus是一个开源的向量数据库,专为AI应用和向量相似度搜索而设计,以加速非结构化数据的检索。自2019年创建以来,Milvus专注于存储、索引和管理由深度神经网络和其他机器学习模型生成的海量嵌入向量。其能够处理万亿级别的向量索引任务。Milvus的核心优势在于其高效的索引机制,它支持多种索引类型,包括FLAT、IVF_FLAT、IVF_SQ8、IVF_PQ和HNSW等。这
- [由浅入深理解神经网络] 2 张量流与反向传播
由浅入深理解神经网络2张量流与反向传播0前言1张量流和运算图2复合函数视角2.1复合函数求导2.1.1链式法则2.1.2多元函数的链式法则2.2前馈网络的反向传播2.3任意网络的反向传播3结语0前言在由浅入深理解神经网络1一个简单到极致的神经网络中,我们已经发现了训练神经网络最重要的一件事,那就是求梯度,然后优化算法利用梯度来调整网络参数.我们重写一下前面提到的一个通用的神经网络:y=f(x;θ)
- 插入表主键冲突做更新
a-john
有以下场景:
用户下了一个订单,订单内的内容较多,且来自多表,首次下单的时候,内容可能会不全(部分内容不是必须,出现有些表根本就没有没有该订单的值)。在以后更改订单时,有些内容会更改,有些内容会新增。
问题:
如果在sql语句中执行update操作,在没有数据的表中会出错。如果在逻辑代码中先做查询,查询结果有做更新,没有做插入,这样会将代码复杂化。
解决:
mysql中提供了一个sql语
- Android xml资源文件中@、@android:type、@*、?、@+含义和区别
Cb123456
@+@?@*
一.@代表引用资源
1.引用自定义资源。格式:@[package:]type/name
android:text="@string/hello"
2.引用系统资源。格式:@android:type/name
android:textColor="@android:color/opaque_red"
- 数据结构的基本介绍
天子之骄
数据结构散列表树、图线性结构价格标签
数据结构的基本介绍
数据结构就是数据的组织形式,用一种提前设计好的框架去存取数据,以便更方便,高效的对数据进行增删查改。正确选择合适的数据结构,对软件程序的高效执行的影响作用不亚于算法的设计。此外,在计算机系统中数据结构的作用也是非同小可。例如常常在编程语言中听到的栈,堆等,就是经典的数据结构。
经典的数据结构大致如下:
一:线性数据结构
(1):列表
a
- 通过二维码开放平台的API快速生成二维码
一炮送你回车库
api
现在很多网站都有通过扫二维码用手机连接的功能,联图网(http://www.liantu.com/pingtai/)的二维码开放平台开放了一个生成二维码图片的Api,挺方便使用的。闲着无聊,写了个前台快速生成二维码的方法。
html代码如下:(二维码将生成在这div下)
? 1
&nbs
- ImageIO读取一张图片改变大小
3213213333332132
javaIOimageBufferedImage
package com.demo;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import javax.imageio.ImageIO;
/**
* @Description 读取一张图片改变大小
* @author FuJianyon
- myeclipse集成svn(一针见血)
7454103
eclipseSVNMyEclipse
&n
- 装箱与拆箱----autoboxing和unboxing
darkranger
J2SE
4.2 自动装箱和拆箱
基本数据(Primitive)类型的自动装箱(autoboxing)、拆箱(unboxing)是自J2SE 5.0开始提供的功能。虽然为您打包基本数据类型提供了方便,但提供方便的同时表示隐藏了细节,建议在能够区分基本数据类型与对象的差别时再使用。
4.2.1 autoboxing和unboxing
在Java中,所有要处理的东西几乎都是对象(Object)
- ajax传统的方式制作ajax
aijuans
Ajax
//这是前台的代码
<%@ page language="java" import="java.util.*" pageEncoding="UTF-8"%> <% String path = request.getContextPath(); String basePath = request.getScheme()+
- 只用jre的eclipse是怎么编译java源文件的?
avords
javaeclipsejdktomcat
eclipse只需要jre就可以运行开发java程序了,也能自动 编译java源代码,但是jre不是java的运行环境么,难道jre中也带有编译工具? 还是eclipse自己实现的?谁能给解释一下呢问题补充:假设系统中没有安装jdk or jre,只在eclipse的目录中有一个jre,那么eclipse会采用该jre,问题是eclipse照样可以编译java源文件,为什么呢?
&nb
- 前端模块化
bee1314
模块化
背景: 前端JavaScript模块化,其实已经不是什么新鲜事了。但是很多的项目还没有真正的使用起来,还处于刀耕火种的野蛮生长阶段。 JavaScript一直缺乏有效的包管理机制,造成了大量的全局变量,大量的方法冲突。我们多么渴望有天能像Java(import),Python (import),Ruby(require)那样写代码。在没有包管理机制的年代,我们是怎么避免所
- 处理百万级以上的数据处理
bijian1013
oraclesql数据库大数据查询
一.处理百万级以上的数据提高查询速度的方法: 1.应尽量避免在 where 子句中使用!=或<>操作符,否则将引擎放弃使用索引而进行全表扫描。
2.对查询进行优化,应尽量避免全表扫描,首先应考虑在 where 及 o
- mac 卸载 java 1.7 或更高版本
征客丶
javaOS
卸载 java 1.7 或更高
sudo rm -rf /Library/Internet\ Plug-Ins/JavaAppletPlugin.plugin
成功执行此命令后,还可以执行 java 与 javac 命令
sudo rm -rf /Library/PreferencePanes/JavaControlPanel.prefPane
成功执行此命令后,还可以执行 java
- 【Spark六十一】Spark Streaming结合Flume、Kafka进行日志分析
bit1129
Stream
第一步,Flume和Kakfa对接,Flume抓取日志,写到Kafka中
第二部,Spark Streaming读取Kafka中的数据,进行实时分析
本文首先使用Kakfa自带的消息处理(脚本)来获取消息,走通Flume和Kafka的对接 1. Flume配置
1. 下载Flume和Kafka集成的插件,下载地址:https://github.com/beyondj2ee/f
- Erlang vs TNSDL
bookjovi
erlang
TNSDL是Nokia内部用于开发电信交换软件的私有语言,是在SDL语言的基础上加以修改而成,TNSDL需翻译成C语言得以编译执行,TNSDL语言中实现了异步并行的特点,当然要完整实现异步并行还需要运行时动态库的支持,异步并行类似于Erlang的process(轻量级进程),TNSDL中则称之为hand,Erlang是基于vm(beam)开发,
- 非常希望有一个预防疲劳的java软件, 预防过劳死和眼睛疲劳,大家一起努力搞一个
ljy325
企业应用
非常希望有一个预防疲劳的java软件,我看新闻和网站,国防科技大学的科学家累死了,太疲劳,老是加班,不休息,经常吃药,吃药根本就没用,根本原因是疲劳过度。我以前做java,那会公司垃圾,老想赶快学习到东西跳槽离开,搞得超负荷,不明理。深圳做软件开发经常累死人,总有不明理的人,有个软件提醒限制很好,可以挽救很多人的生命。
相关新闻:
(1)IT行业成五大疾病重灾区:过劳死平均37.9岁
- 读《研磨设计模式》-代码笔记-原型模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
/**
* Effective Java 建议使用copy constructor or copy factory来代替clone()方法:
* 1.public Product copy(Product p){}
* 2.publi
- 配置管理---svn工具之权限配置
chenyu19891124
SVN
今天花了大半天的功夫,终于弄懂svn权限配置。下面是今天收获的战绩。
安装完svn后就是在svn中建立版本库,比如我本地的是版本库路径是C:\Repositories\pepos。pepos是我的版本库。在pepos的目录结构
pepos
component
webapps
在conf里面的auth里赋予的权限配置为
[groups]
- 浅谈程序员的数学修养
comsci
设计模式编程算法面试招聘
浅谈程序员的数学修养
- 批量执行 bulk collect与forall用法
daizj
oraclesqlbulk collectforall
BULK COLLECT 子句会批量检索结果,即一次性将结果集绑定到一个集合变量中,并从SQL引擎发送到PL/SQL引擎。通常可以在SELECT INTO、
FETCH INTO以及RETURNING INTO子句中使用BULK COLLECT。本文将逐一描述BULK COLLECT在这几种情形下的用法。
有关FORALL语句的用法请参考:批量SQL之 F
- Linux下使用rsync最快速删除海量文件的方法
dongwei_6688
OS
1、先安装rsync:yum install rsync
2、建立一个空的文件夹:mkdir /tmp/test
3、用rsync删除目标目录:rsync --delete-before -a -H -v --progress --stats /tmp/test/ log/这样我们要删除的log目录就会被清空了,删除的速度会非常快。rsync实际上用的是替换原理,处理数十万个文件也是秒删。
- Yii CModel中rules验证规格
dcj3sjt126com
rulesyiivalidate
Yii cValidator主要用法分析:
yii验证rulesit 分类: Yii yii的rules验证 cValidator主要属性 attributes ,builtInValidators,enableClientValidation,message,on,safe,skipOnError
- 基于vagrant的redis主从实验
dcj3sjt126com
vagrant
平台: Mac
工具: Vagrant
系统: Centos6.5
实验目的: Redis主从
实现思路
制作一个基于sentos6.5, 已经安装好reids的box, 添加一个脚本配置从机, 然后作为后面主机从机的基础box
制作sentos6.5+redis的box
mkdir vagrant_redis
cd vagrant_
- Memcached(二)、Centos安装Memcached服务器
frank1234
centosmemcached
一、安装gcc
rpm和yum安装memcached服务器连接没有找到,所以我使用的是make的方式安装,由于make依赖于gcc,所以要先安装gcc
开始安装,命令如下,[color=red][b]顺序一定不能出错[/b][/color]:
建议可以先切换到root用户,不然可能会遇到权限问题:su root 输入密码......
rpm -ivh kernel-head
- Remove Duplicates from Sorted List
hcx2013
remove
Given a sorted linked list, delete all duplicates such that each element appear only once.
For example,Given 1->1->2, return 1->2.Given 1->1->2->3->3, return&
- Spring4新特性——JSR310日期时间API的支持
jinnianshilongnian
spring4
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- 浅谈enum与单例设计模式
247687009
java单例
在JDK1.5之前的单例实现方式有两种(懒汉式和饿汉式并无设计上的区别故看做一种),两者同是私有构
造器,导出静态成员变量,以便调用者访问。
第一种
package singleton;
public class Singleton {
//导出全局成员
public final static Singleton INSTANCE = new S
- 使用switch条件语句需要注意的几点
openwrt
cbreakswitch
1. 当满足条件的case中没有break,程序将依次执行其后的每种条件(包括default)直到遇到break跳出
int main()
{
int n = 1;
switch(n) {
case 1:
printf("--1--\n");
default:
printf("defa
- 配置Spring Mybatis JUnit测试环境的应用上下文
schnell18
springmybatisJUnit
Spring-test模块中的应用上下文和web及spring boot的有很大差异。主要试下来差异有:
单元测试的app context不支持从外部properties文件注入属性
@Value注解不能解析带通配符的路径字符串
解决第一个问题可以配置一个PropertyPlaceholderConfigurer的bean。
第二个问题的具体实例是:
- Java 定时任务总结一
tuoni
javaspringtimerquartztimertask
Java定时任务总结 一.从技术上分类大概分为以下三种方式: 1.Java自带的java.util.Timer类,这个类允许你调度一个java.util.TimerTask任务; 说明: java.util.Timer定时器,实际上是个线程,定时执行TimerTask类 &
- 一种防止用户生成内容站点出现商业广告以及非法有害等垃圾信息的方法
yangshangchuan
rank相似度计算文本相似度词袋模型余弦相似度
本文描述了一种在ITEYE博客频道上面出现的新型的商业广告形式及其应对方法,对于其他的用户生成内容站点类型也具有同样的适用性。
最近在ITEYE博客频道上面出现了一种新型的商业广告形式,方法如下:
1、注册多个账号(一般10个以上)。
2、从多个账号中选择一个账号,发表1-2篇博文