【动手学深度学习PyTorch版】19 含并行连结的网络 GoogLeNet / Inception V3

上一篇请移步【动手学深度学习PyTorch版】17 深度卷积神经网络 AlexNet_水w的博客-CSDN博客【动手学深度学习PyTorch版】18 使用块的网络 VGG_水w的博客-CSDN博客【动手学深度学习PyTorch版】17 深度卷积神经网络 AlexNet_水w的博客-CSDN博客

目录

 一、Inception块

◼ Inception块的通道数

◼ 为什么要用Inception块？

◼ Inception块有各种后续变种

二、GoogLeNet

◼ GoogLeNet架构

具体结构：

三、总结

四、GoogLeNet（使用自定义）

---

GoogLeNet在2014年ImageNet图像识别挑战赛中大放异彩。虽然NiN现在基本上没有被使用了，但是GoogLeNet现在还是大量地被使用。

GoogLeNet是第一次做到快100层卷积层（第一个做到超过100层的卷积神经网络，这里不是说有100层深，而是说网络中卷积层的个数超过了100）。GoogLeNet名字中的L是大写的，也是为了致敬LeNet，虽然它跟LeNet并没有什么关系。

GoogLeNet的设计受到了NiN很大的影响，吸收了NiN中串联网络的思想，并在此基础上做了改进。

 

 一、Inception块

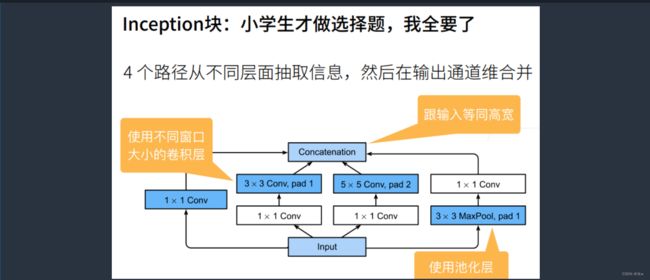
GoogLeNet中最重要的是Inception块，在这个块中抽取了不同的通道，不同的通道有不同的设计，如下图所示，Inception块通过四条路经从不同的层面抽取信息，然后在输出通道维合并：

• 前三条路径使用窗口大小为1 * 1、3 * 3、5 * 5的卷积层，从不同的空间大小中提取信息；
• 中间两条路径在输入上执行1 * 1卷积，以减少通道数，从而降低模型的复杂性；
• 第四条路经使用3 * 3最大汇聚层Maxpooling，然后使用1 * 1卷积层来改变通道数；
• 四条路径都是用合适的填充来使输入和输出的高宽一致；
• 最后每条线路的输出在通道维度上连结，得到Inception块的输出；
• 在Inception块中，通常调整的超参数是每层输出通道数；

具体过程：

首先，输入被复制成了四块（之前所遇到的都是一条路直接到最后）：

• 第一条路先进入一个1 *1的卷积层再输出；
• 第二条路先通过一个1 * 1的卷积层对通道做变换，再通过一个pad为1的3 * 3的卷积层，使得输入和输出的高宽相同；
• 第三条路先通过一个1 * 1的卷积层对通道数做变换，不改变高宽，但是再通过一个pad为2的5 * 5的卷积层提取空间信息特征，输入和输出还是等高等宽的；
• 第四条路先通过一个pad为1的3 * 3的最大池化层Maxpooling，再通过一个1 * 1的卷积层；

因为这四条路都没有改变高宽，最后用一个contact的操作将它们的输出合并起来（不是将四张图片放在一起形成一张更大的图片，而是在输出的通道数上做合并，最终的输出和输入等同高宽，但是输出的通道数更多，因为是四条路输出的通道数合并在一起的），因此，输出的高宽是不变的，改变的只有它的通道数。

我们反过来再看，这里面有1 *1的卷积层，3 * 3的卷积层，3 * 3的最大池化层等等，基本上都有看了。在这个结构中，基本上各种形状的卷积层和最大池化层等都有了，所以就不用过多地纠结于卷积层尺寸的选择。

为什么GoogLeNet这么有效？

• 滤波器（filter）的组合：可以使用各种不同的滤波器尺寸探索图像，这就意味着不同大小的滤波器可以有效地识别不同范围的图像细节；
• 可以为不同的滤波器分配不同数量的参数；

◼ Inception块的通道数

假设输入的通道数是192，高宽是28 * 28.

因为在Inception块中，高宽是不变的，所以上图中只标出了通道数的变化：

（1）通过第一条路时，经过第一个卷积层直接将通道数压缩到了64

（2）经过第二条路时，先经过一个1 * 1的卷积层将通道数从192压缩到了96（这里为什么要压缩到96？

因为想要把后一层3 * 3的卷积层的输入数降低，通过降低输入通道数来降低模型的复杂度，因为模型复杂度可以认为是可以学习的参数的个数，卷积层可学习参数的个数是输入通道 * 输出通道 * 卷积核的大小（3 * 3），所以这里要将192压缩为96），然后再经过一个3 * 3的卷积层后，通道数增加到128。

（3）经过第三条路时，先通过一个3 * 3的卷积层将通道数压缩到16，再经过一个5 * 5的卷积层（这里分配的通道数并不多）增加到32。

（4）经过第四条路时，首先经过一个3 * 3的最大池化层Maxpooling，这里并不会改变通道数，然后经过一个1 * 1的卷积层之后，通道数直接由192降到了32。

总的来说，上图中标记为白色的卷积层可以认为是用来改变通道数的，要么改变输入，要么改变输出；标记为蓝色的卷积层，我们可以认为是用来抽取信息的。

• 第1条路中标记为蓝色的卷积层不抽取空间信息，只抽取通道信息，
• 第2、3条路中标记为蓝色的卷积层是用来抽取空间信息的，
• 第4条路中标记为蓝色的最大池化层Maxpooling也是用来抽取空间信息的，增强鲁棒性。

经过Inception块之后，最后输出的通道数由输入的192变成了64+128+32+32=256，每个通道都会识别一些特定的模型，所以应该把重要的通道数留给重要的通道（这里的意思应该是类似于：输入进来之后被复制成了四份，然后经过四条不同的路，最终进行通道数的合并，在输出通道数固定的情况下，四条路的最终输出的通道数是不一样的，所以可以将有限的输出通道数分配给不同的路径，有一点像权重。

就比如上图中给第二条路分配了128个输出通道数，接近一半的通道数都留给了3 * 3的卷积层，因为3 * 3的卷积层计算量不大，同时能够很好地抽取信息，剩下通道数的一半分给了1 * 1的卷积层，然后再剩下给第3、4条路平分）。

大致的设计思路就是这样，但是具体所使用的数值也是调出来的。

◼ 为什么要用Inception块？

假设输入是64，输出是128，

• 如果使用Inception的话，模型参数大概有0.16M。
• 如果只用3 * 3的卷积而不用Inception块的话，模型参数大概有0.44M。
• 如果只用5 * 5的卷积而不用Inception块的话，模型参数大概有1.22M（卷积窗口变大了，所以模型参数变多了）。

输出相同的通道数，5X5比3X3的卷积层参数个数多，3X3比1X1卷积层的参数个数多。

Inception块使用了大量1X1卷积层，使得参数相对单3X3、5X5卷积层更少。

由此可以得出，Inception确实通过各种块的设计以及通过1 * 1的卷积层来降低通道数，从而使得参数数量和计算量大幅度减少了。

Inception的优点：不仅增加了网络结构的多样性（有大量不同设置的卷积层），而且参数数量和计算量都显著降低了 。

◼ Inception块有各种后续变种

 

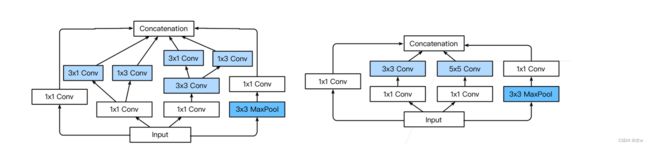上图中右边是原始的Inception块，左边是Inception V3块 。

圈的大小表示耗内存的大小。

Inception V3的模型效果如上图所示，图中X轴表示处理的速度（log分布，越往右越快），从图中可以看出Inception V3还算是比较慢，每秒钟大概能够跑800个样本（仅仅是预测，训练的话会更慢）。

图中Y轴表示精度，可以看出Inception V3的精度还是比较高的，在ImageNet上的精度达到了0.8左右，虽然它所占用的内存比较多（图中园区那的大小表示所占用的内存的大小），运算比较慢，但是它的精度是完胜VGG的（和现在的一些网络比较起来其实没有太大的优势，但是当年的效果还是很好的）。

Inception V4：使用残差连接。

二、GoogLeNet

◼ GoogLeNet架构

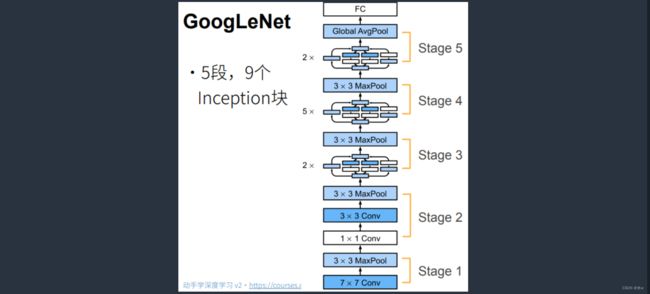
GoogLeNet一共使用了9个Inception块和全局平均汇聚层（避免在最后使用全连接层）的堆叠来生成估计值，第一个模块类似于AlexNet和LeNet，Inception块的组合从VGG继承。

•  Inception块之间的最大汇聚层可以降低维度，
• GoogLeNet由大量的Inception块组成，如上图所示，总共分成了5个stage（有点类似于VGG，高宽减半一次为1个stage）。
• GoogLeNet中总共有9个Inception块，主要集中在stage 3（2个）、stage 4（5个）和stage 5（2个）。
• GoogLeNet中大量地使用了1 * 1的卷积，把它当成全连接来使用，来做通道数的变换（受到NiN的影响）。
• GoogLeNet中也使用了全局平均池化层。

因为最后没有设置Inception块使得最后的输出通道数等于标签的类别数，所以在倒数第二步做完全局平均池化之后会拿到一个长为通道数的向量，最后再通过一个全连接层映射到标号所要的类别数（这里并没有强求最后的输出通道数一定要等于标签类别数，做了简化，更加灵活）。

具体结构：

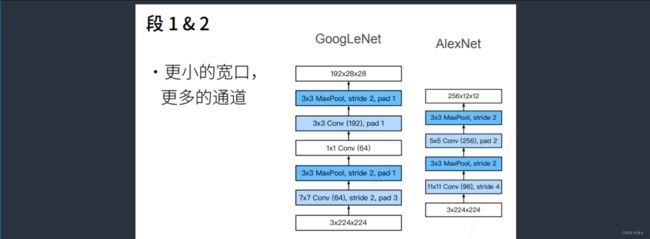
1、Stage 1：第一个模块使用了一个卷积层和一个最大池化层，

• 第一个模块先使用了一个64通道7 * 7的卷积层（stride = 2，padding = 3）；
• 然后使用了一个3 * 3的最大池化层（stride = 2，padding = 1）；

2、Stage 2：第二个模块使用了两个卷积层和一个最大池化层，

• 第一个卷积层是64通道1 * 1的卷积层（降低通道数）；
• 第二个卷积层是192通道的3 * 3的卷积层（stride = 3，padding = 1）；
• 最大池化层的窗口大小为3 * 3（stride = 2，padding = 1）；

3、Stage 3：第三个模块串联了两个完整的Inception块和一个最大池化层，

• 第一个Inception块的输出通道数为：64 + 128 + 32 + 32 = 256，四条路经之间的输出通道数量比是：64 ：128 ：32 ：32 = 2 ：4 ：1 ：1。第二条和第三条路径首先将输入通道的数量分别由192减少到96和16，然后连接第二个卷积层（Inception（192，64，（96，128），（16，32），32））；
• 第二个Inception块的输出通道数增加到128 + 192 + 96 + 64 = 480，四条路经之间的输出通道数量比为128 ：192 ：96 ：64 = 4 ：6 ：3 ：2，第二条和第三条路径首先将输入通道数量分别由256减少到128和32，然后连接第二个卷积层（Inception（256，128，（128，192），（32，96），64））；
• 最大池化层的窗口大小为3 * 3（stride = 2，padding = 1）

4、Stage 4：第四个模块串联了5个Inception块和一个最大池化层，

• 第一个Inception块的输出通道数为：192 + 208 + 48 + 64 = 512（Inception（480，192，（96，208），（16，48），64））；
• 第二个Inception块的输出通道数为：160 + 224 + 64 + 64 =512（Inception（512，160，（112，224），（24，64），64））；
• 第三个Inception块的输出通道数为：128 + 256 + 64 + 64 = 512（Inception（512，128，（128，256），（24，64），64））；
• 第四个Inception块的输出通道数为：112 + 288 + 64 + 64 =528 （Inception（512，112，（144，288），（32，64），64））；
• 第五个Inception块的输出通道数为：256 + 320 +128 + 128 = 832（Inception（528，256，（160，320），（32，128），128））；

以上这些路径的通道数分配和和第三模块中的类似

• 第一条路经仅含1 * 1的卷积层；
• 含3 * 3卷积层的第二条路径输出最多通道；
• 含5 * 5卷积层的第三条路经；
• 含3 * 3最大汇聚层的第四条路经；
• 第二、第三条路径都会先按比例减小通道数；

5、Stage 5：第五个模块中有两个Inception块和一个输出层，

• 第一个Inception块的输出通道数为：256 + 320 + 128 +128 = 832（Inception（832，256，（160，320），（32，128），128））；
• 第二个Inception块的输出通道数为：384 + 384 + 128 +128 = 1024（Inception（832，384，（192，384），（48，128），128））；
• 输出层和NiN一样使用全局平均汇聚层，将每个通道的高和宽变成1；
• 最后将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层 nn.Linear（1024，10）；

以上这些路径通道数的分配思路和第三、第四模块一致。

三、总结

（1）Inception块有四条不同超参数的卷积层和池化层的路来抽取不同的信息（等价于一个有4条路径的子网络，通过不同窗口形状的卷积层和最大汇聚层来并行抽取信息，并使用1 * 1卷积层减少每像素级别上的通道维数从而降低模型的复杂度）。

它的一个主要优点是模型参数小，计算复杂度低。

（2）GoogLeNet使用了9个Inception块（每个Inception块中有6个卷积层，所有Inception块中一共有54个卷积层），这些Inception块与其他层（卷积层、全连接层）串联起来。

其中Inception块的通道数分配之比是在Imagenet数据集上通过大量的实验得来的。

（3）GoogLeNet是第一个达到上百层的网络，但是不是深度是100，直到ResNet的出现才达到了模型的深度达到100层，这里的上百层指的是通过设计并行的通道来使得模型达到数百层。

（4）Inception后续也有一系列的改进，GoogLeNet V3和GoogLeNet V4目前依旧在被使用，GoogLeNet一开始的精度其实不高，在BN、V3、V4之后精度才慢慢提升上去了，现在也是比较常用的模块，它以较低的计算复杂度提供了类似的测试精度。

（5）GoogLeNet的问题是特别复杂，通道数的设置没有一定的选择依据，以及内部构造比较奇怪，这也是GoogLeNet不那么受欢迎的原因所在。

四、GoogLeNet（使用自定义）

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Inception(nn.Module):
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs): # c1为第一条路的输出通道数、c2为第二条路的输出通道数     
        super(Inception, self).__init__(**kwargs) # python中*vars代表解包元组，**vars代表解包字典，通过这种语法可以传递不定参数。**kwage是将除了前面显式列出的参数外的其他参数, 以dict结构进行接收.                                                    
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0],c3[1],kernel_size=5,padding=2)
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels,c4,kernel_size=1)
        
    def forward(self, x):
        p1 = F.relu(self.p1_1(x))  # 第一条路的输出
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x)))) # 第二条路的输出
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1, p2, p3, p4), dim=1) # 批量大小的dim为0，通道数的dim为1，以通道数维度进行合并

 

b1 = nn.Sequential(nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
                  nn.ReLU(),nn.MaxPool2d(kernel_size=3,stride=2,padding=1))  

b2 = nn.Sequential(nn.Conv2d(64,64,kernel_size=1),nn.ReLU(),
                  nn.Conv2d(64,192,kernel_size=3,padding=1),
                  nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

b3 = nn.Sequential(Inception(192,64,(96,128),(18,32),32),
                  Inception(256,128,(128,192),(32,96),64),
                  nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

b4 = nn.Sequential(Inception(480,192,(96,208),(16,48),64),
                  Inception(512,160,(112,224),(24,64),64),
                  Inception(512,128,(128,256),(24,64),64),
                  Inception(512,112,(144,288),(32,64),64),
                  Inception(528,256,(160,320),(32,128),128),
                  nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

b5 = nn.Sequential(Inception(832,256,(160,320),(32,128),128),
                   Inception(832,384,(192,384),(48,128),128),
                  nn.AdaptiveAvgPool2d((1,1)),nn.Flatten())

net = nn.Sequential(b1,b2,b3,b4,b5,nn.Linear(1024,10))

在实际的项目当中，我们往往预先只知道的是输入数据和输出数据的大小，而不知道核与步长的大小。

我们可以手动计算核的大小和步长的值。而自适应（Adaptive）能让我们从这样的计算当中解脱出来，只要我们给定输入数据和输出数据的大小，自适应算法能够自动帮助我们计算核的大小和每次移动的步长。

相当于我们对核说，我已经给你输入和输出的数据了，你自己适应去吧。你要长多大，你每次要走多远，都由你自己决定，总之最后你的输出符合我的要求就行了。

比如我们给定输入数据的尺寸是9， 输出数据的尺寸是3，那么自适应算法就能自动帮我们计算出，核的大小是3，每次移动的步长也是3，然后依据这些数据，帮我们创建好池化层。

# 对输入应用自适应平均池化，将feature map改为我们需要大小的输出。只需要给定输出特征图的大小就好，其中通道数前后不发生变化。  
help(nn.AdaptiveAvgPool2d)                   

为了使Fashion-MNIST上的训练短小精悍，我们将输入的高和宽从224降到96.

# 为了使Fashion-MNIST上的训练短小精悍，我们将输入的高和宽从224降到96
X = torch.rand(size=(1,1,96,96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(), nn.MaxPool2d(kernel_size=3, stride=2,
                                           padding=1))

b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1, 1)), nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

lr, num_epochs, batch_size =0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size,resize=96)  
d2l.train_ch6(net,train_iter,test_iter,num_epochs,lr,d2l.try_gpu())

精度还是不错的。