Pytorch ---- 线性模型 学习笔记~~~~~
线性公式 y = w * x (w为权重)
MSE: 均方误差 (一种回归损失函数) 当前权重下所有X数据计算出来的y数据(预测数据)和真实的y数据之间的差的平方 除以X的样本数量。
MSE越小,说明预测值Y和真实值Y之间误差越小。即当前权重越合理。
例子:
给定数据:
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
使用穷举法寻找0~4之间最合适的值。
最后使用 matplotlib绘图即可。
代码实现:
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
# 计算预测值
def predict(x, w):
num_pre = x * w
return num_pre
# 计算损失值
def loss(num_pre, y_val):
num_loss = (num_pre - y_val) * (num_pre - y_val)
return num_loss
w_ll = [] # 权重列表
mse_ll = [] # 均方误差列表
loss_sum = 0 # 计算本回合内的损失总量
# 穷举权重
if __name__ == '__main__':
for w in np.arange(0.0,4.1,0.1):
w = round(w,1)
print("当前的权重值w为:", w)
for x_val, y_val in zip(x_data, y_data):
num_pre = predict(x_val, w) # 拿到当前穷举的预测值
num_loss = loss(num_pre, y_val) # 那预测值去计算损失值
loss_sum += num_loss
w_ll.append(w)
mse_ll.append(loss_sum / len(x_data))
loss_sum = 0
print(w_ll)
print(mse_ll)
plt.rcParams['font.sans-serif'] = ['KaiTi']
plt.plot(w_ll,mse_ll)
plt.xlabel("权重W")
plt.ylabel("MSE")
plt.show()
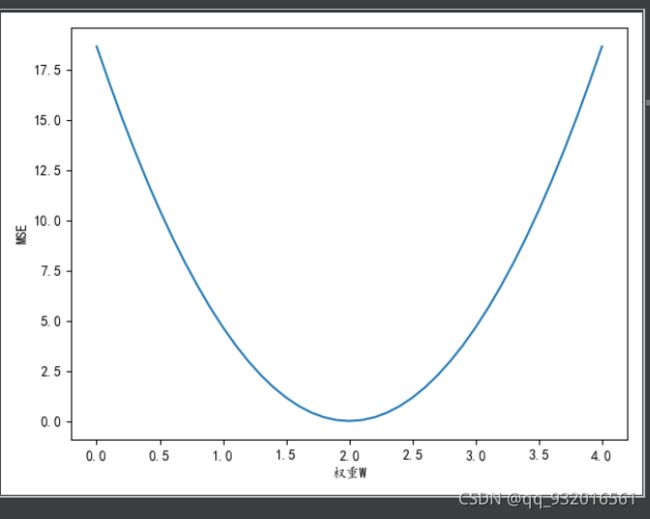
得到最终结果:
X轴为权重,Y轴为MSE。
可以看到权重为2的时候。MSE最小。
这里有个坑,使用 np.arange 有双浮点数精度损失。
for i in np.arange(0.0,4.0,0.1):
print(i)
部分输出:
0.0
0.1
0.2
0.30000000000000004
0.4
0.5
0.6000000000000001
0.7000000000000001
0.8
0.9
1.0
1.1
1.2000000000000002
1.3
1.4000000000000001
1.5
1.6
1.7000000000000002
1.8
这里可以看到有一些非常微小的精度问题,虽然对本题结果基本不构成影响,但是如果数据变得异常大不知道会不会有影响。
而后换成linspace 函数后存在同样的问题。直接使用linspace进行分配不会产生精度问题,而将其放入循环就会产生精度问题,有知道怎么处理的小伙伴,可以给我留言教教我~~~。
在本题中处理精度损失的方法是,直接截取了小数点后一位数。