COMBINING LABEL PROPAGATION AND SIMPLE MODELS OUT-PERFORMS GRAPH NEURAL NETWORKS（Correct&Smooth）阅读笔记

 文章目录

• 链接
• 一、摘要
• 二、引言
• 三、“修正和平滑"模型
• 四、转导式节点分类实验
• 四、总结
• 总结

红色部分为个人的一些解读，不足之处请多多指点！

---

链接

论文题目：结合标签传播和简单模型的超性能图形神经网络（FDiff-scale）（2021ICLR）

论文链接：2010.13993.pdf (arxiv.org)

代码链接：GitHub - CUAI/CorrectAndSmooth: [ICLR 2021] Combining Label Propagation and Simple Models Out-performs Graph Neural Networks (https://arxiv.org/abs/2010.13993)

作者讲解：Qian Huang, Horace He, Abhay Singh, Ser-Nam Lim, Austin Benson · Combining Label Propagation and Simple Models Out-Performs Graph Neural Networks · SlidesLive

一、摘要

        图神经网络（GNN）是图学习的主要技术。然而，人们对GNN在实践中取得成功的原因以及它们是否是良好性能所必需的了解相对较少。在这里，我们表明，对于许多标准的归纳节点分类基准，我们可以通过将忽略图结构的浅层模型与利用标签结构中的相关性的两个简单的后处理步骤相结合，来超过或匹配最先进的GNN的性能：（i）"错误相关性"，将训练数据中的残余错误分散到测试数据中的纠正错误；（ii）"预测相关性"，使测试数据中的预测变得平滑。我们把这个整体程序称为 "修正和平滑"（C&S），后处理步骤是通过对早期基于图的半监督学习方法的标准标签传播技术的简单修改来实现。我们的方法在各种各样的基准上超过或几乎达到了最先进的GNN的性能，而参数只是一小部分，运行时间却快了几个数量级。例如，在OGB-产品数据集上，我们以少137倍的参数和多于100倍的训练时间超过了已知的最佳GNN性能。我们的方法的性能强调了直接将标签信息纳入学习算法（就像传统技术中所做的那样）是如何产生轻松和可观的性能提升的。我们还可以将我们的技术纳入大的GNN模型中，提供适度的收益。我们关于OGB结果的代码在：GitHub - CUAI/CorrectAndSmooth: [ICLR 2021] Combining Label Propagation and Simple Models Out-performs Graph Neural Networks (https://arxiv.org/abs/2010.13993)

        该文章关键点在于标签传播，何为标签传播？我们首先要知道GNN需要两个操作，聚合和更新，原始的GNN模型是聚合、更新、聚合、更新...这样反复迭代，而标签传播是先重复更新操作，得出每个节点的标签，然后拿标签去做聚合，这就是标签传播。

二、引言

        继神经网络在计算机视觉和自然语言处理方面取得成功之后，现在出现了广泛的图神经网络（GNN），用于进行涉及关系数据的预测（Battaglia等人，2018；Wu等人，2020）。这些模型取得了很大的成功，并位居排行榜前列，如开放图形基准（Hu等人，2020年）。通常，GNN的方法开发围绕着创建比基本变体更具表现力的架构而展开，例如图卷积网络（GCN）（Kipf&Welling，2017）或GraphSAGE（Hamilton等人，2017a）；示例包括图注意力网络（V eli´ckovi´c等人，2018）、图同构网络（Xu等人，2018年）和各种深度模型（Li等人，2019年；Rong等人，201九年；Chen等人，2020年）。新GNN架构的许多想法都是从语言（如注意力）或视觉（如深度CNN）模型中的新架构改编而来的，希望成功能转化为图形。然而，随着这些模型变得越来越复杂，理解它们的性能提升是一个重大挑战，并且很难将它们扩展到大型数据集。

        在这里，我们看到通过结合更简单的模型，我们能走多远，重点是了解在图学习中哪些地方容易有机会提高性能，特别是过渡性节点分类。我们提出了一个简单的通道，有三个主要部分（图1）。(i) 用节点特征做出的基础预测，忽略了图的结构（如MLP或线性模型）；(ii) 修正步骤，将训练数据的不确定性传播到整个图中，以修正基础预测；(iii)对整个图预测的平滑处理。步骤(ii)和(iii)只是后处理，使用了基于图的半监督学习的经典方法，即标签传播(朱，2005)。通过对这些经典思想的一些修改和新的部署，我们在几个节点分类任务上获得了最先进的性能，性能超过了大型GNN模型。在我们的框架中，图结构不是用来学习参数的，而是作为一种后处理机制。这种简单性导致了具有数量级的模型、更少的参数、更少的训练时间，并且可以很容易地扩展到大型图表。我们还可以将我们的想法与最先进的GNN相结合，并看到适度的性能提升。

         图1：无GNN模型的总览，正确和平滑的一个示例。左侧簇属于橙色，右侧簇属于蓝色。我们使用MLP进行基本预测，忽略了图结构，我们假设在本例中，图结构对所有节点的预测都是相同的。之后，通过传播来自训练数据的错误，对基础预测进行修正。最后，修正后的预测通过标签传播进行平滑处理。

        MLP就相当于GNN只做了更新的操作， 用公式来表示的话，原始GCN模型​中的就是更新操作，而就是聚合操作。

        我们性能改进的一个主要来源是直接使用标签进行预测。这种想法并不新鲜，早期在图上基于扩散的半监督学习算法，如转导式谱图(Joachims，2003)、高斯随机场模型(朱等人，2003)和标签扩散(周等人，2004)都使用这种思想。然而，这些方法的动机是对点云数据进行半监督学习，因此使用特征来构建图形。从那时起，这些技术被用于仅从标签(即没有特征)学习关系数据(Koutra等人，2011年；Gleich&MaHony，2015；Peel，2017；Chin等人，2019年)，但在GNN中基本上被忽略了。话虽如此，我们发现，即使是简单的标签传播(忽略功能)在许多基准测试中也表现得出奇地好。这为组合预测能力的两个正交来源提供了动力，一个来自节点特征(忽略图结构)，另一个来自直接在预测中使用已知标签。

        最近的研究将GNN与标签传播联系起来(Wang&Leskovec，2020；Jia&Benson，2020)以及马尔可夫随机场(Qu等人，2019；Gao等人，2019)，一些技术使用在特征中特别结合标签信息(Shih等人，2020)。然而，这些方法的培训成本仍然很高，而我们以两种可以理解的低成本方式使用标签传播。我们从一个忽略图结构的模型开始一个廉价的“基本预测”(可能除了一个廉价的预处理特征增强步骤，如谱嵌入)。之后，我们使用标签传播进行纠错，然后平滑最终预测。这些后处理步骤基于这样一个事实，即连接节点上的错误和标签是正相关的。假设连接节点之间的相似性是许多网络分析的中心，并对应于同源或分类混合(McPherson等人，2001；Newman，2003；Easley&Kleinberg，2010)。在半监督学习文献中，类似的是光滑性或聚类假设(Chapelle等人，2003；朱，2005)。我们在各种各样的数据集上看到的标签传播的良好性能表明，这些相关性适用于共同的基准。

        总体而言，我们的方法表明，结合几个简单的想法，在模型大小(即参数数量)和训练时间方面，以很小的代价获得了极好的转导节点分类性能。例如，在OGB-Products（该数据集出自OGB，有2449029个节点，61859140条边，是图神经网络中节点分类任务的一个大规模数据集）基准上，我们的性能优于目前最知名的GNN，参数减少了两个数量级以上，训练时间减少了两个数量级以上。然而，我们的目标并不是说当前的图学习方法很差或不合适。相反，我们的目标是强调在图形学习中提高预测性能的更容易的方法，并更好地理解性能收益的来源。我们的主要发现是，更直接地将标签纳入学习算法是关键。通过将我们的想法与现有的GNN相结合，我们也看到了改进，尽管这些改进很小。我们希望我们的方法激发新的想法，可以帮助其他图学习任务，如归纳节点分类，链接预测，和图预测。

2.1 其他相关工作

        (APPNP)（对应这篇论文里面提出的TTPP操作《Model Degradation Hinders Deep Graph Neural Networks》）框架与我们的工作最相关，因为它们也平滑了基本预测(Klicpera等人，2018年)。然而，他们专注于将这种平滑集成到训练过程中，以便可以端到端地训练他们的模型。这不仅大大增加了计算成本，还阻止了APPNP在推理时合并标签信息。与APPNP相比，我们的框架产生了更准确的预测，训练速度更快，更容易扩展到大型数据集。我们的框架还补充了简化的图卷积(Wu等人，2019年)，以及旨在增加可扩展性的算法(Bojchevski等人，2020年；Zeng等人，2019年；Rossi等人，2020年)。然而，我们方法的主要焦点是直接使用标签，而可伸缩性是一个副产品。也有连接GCNS和标签传播的先前工作。Wang&Leskovec(2020)使用标签传播作为对GNN的边缘加权的预处理步骤，而我们使用标签传播作为后处理步骤来避免GNN。Jia&Benson(2020)将标签传播与GNN一起用于回归任务，我们的纠错步骤适应了他们的一些想法，用于分类。最后，最近有几种方法将非线性引入到标签传播方法中，以与GNN竞争并实现可伸缩性(Eiliv&Cohen，2018；Ibrahim&Gleich，2019；Tudisco等人，2020)，但这些方法侧重于低标签率的设置，没有纳入特征学习。

三、修正和平滑模型

        我们从一些符号开始。我们假设我们有一个无向图，其中有个节点，每个节点上的特征由一个矩阵表示。设是图的邻接矩阵，是对角矩阵，是归一化邻接矩阵。对于预测问题，节点集被分成一个不相交的未标记节点和标记节点的集合，它们是索引。我们用一个独热编码矩阵来表示标签，其中是类别的数量(即，如果在类别中，则，否则为)，并且我们进一步将标签节点分割成训练集和验证集。我们的问题是转导节点分类：（归纳学习与我们通常所知的传统监督机器学习是一样的。我们基于已有标记的训练数据集构建和训练机器学习模型。然后我们使用这个训练过的模型来预测我们的测试数据集的标签。与归纳学习相反，转导学习技术事先观察了所有的数据，包括训练数据集和测试数据集。我们从已经观察到的训练数据集中学习，然后预测测试数据集的标签。即使我们不知道测试数据集的标签，我们也可以在学习过程中利用这些数据中的模式和其他信息。）给定和,为每个在中的节点分类。

        我们的方法从一个简单的基于节点特征的基本预测器开始，它不依赖于对图的任何学习。之后，我们执行两种类型的标签传播(LP)：一种是通过对相关误差建模来修正基本预测，另一种是平滑最终预测。我们称这两种方法的结合为：修正和平滑(C&S；图1)。LP只是后处理步骤，我们的通道没有经过端到端（端到端指使用者直接输入原始材料，直接得到可用的结果，而不用去关心中间的产物。如传入照片，结果就是直接识别出多个人脸，而不是在中间添加一些额外人工操作，如人工划定范围，人工设计特征等）的培训。此外，该图仅用于这些后处理步骤以及用于增强特征的预处理步骤，而不用于基本预测。与标准GNN模型相比，这使得训练速度更快且可扩展。此外，我们利用了LP(在没有功能的情况下，它本身往往执行得相当好)和节点功能。我们将看到，将这些互补信号组合在一起会产生出色的预测。

3.1 简单的基础预测器

        首先，我们使用一个不依赖图结构的简单基础预测器。更具体地说，我们训练一个模型f来最小化，其中是的第行，是的第行，而是一个损失函数。在本文中，是一个线性模型或一个浅层多层感知器（MLP），然后是一个softmax，而是交叉熵损失。验证集用于调整超参数，如学习率和MLP的隐藏层维度。从中，我们得到一个基础预测，其中的每一行是由softmax产生的概率分布。省略这些图结构的基础预测可以避免GNN的可扩展性问题。但原则上，我们可以对使用任何基础预测器，包括那些基于GNN的预测器，我们将在第3节对此进行探讨。然而，为了使我们的通道简单和可扩展，我们只使用线性分类器或MLPs，并进行后续的后处理，这一点我们将在接下来描述。

        最终的基础预测，大小为,是节点数，是每个节点的维度，一般来说节点维度的大小和数据集的类别一样，比如说某数据集有六个类别，最终的基础预测就是六维的向量，向量里面的每个元素代表该节点是该类别的概率，这六个概率那个最大，模型就认定该节点属于这个类别。

3.2 用残差传播纠正基础预测的错误

        接下来，我们通过加入标签来改善基础预测的准确性，使其与错误相关联。关键的想法是，我们希望基础预测中的错误能沿着图中的边正向相关起来。换句话说，节点的错误会增加的邻近节点出现类似错误的机会。我们这里的方法部分受到了残差传播的启发（Jia & Benson, 2020），其中一个类似的概念被用于节点回归任务，以及更广泛的广义最小二乘法和相关误差模型（Shalizi, 2013）。

        为此，我们首先定义一个误差矩阵，其中误差是训练数据上的残差，其他地方为零:

(1)

        只有当基础预测器做出完美预测时，中对应于训练节点的残差才为零。我们使用Zhou等人（2004）的标签扩散技术平滑误差。(2004)的标签扩散技术，对目标进行优化

(2)

        第一项鼓励对图的误差估计的平滑性，等于，其中是的第列。第二项使解决方案接近于误差的初始猜测。与Zhou等人（2004）一样，可以通过迭代得到解，其中，，迅速收敛于。这个迭代是误差的扩散、传播或蔓延，我们将平滑的误差加到基础预测中，得到修正的预测值。我们强调，这是一种后处理技术，没有与基础预测耦合训练。

        在高斯假设下，这种传播方式被证明是回归问题中正确的方法（Jia & Benson, 2020）；然而，对于我们考虑的分类问题，平滑的误差可能不在正确的尺度。我们知道，在一般情况下。

(3)

        当时，我们就会发现。因此，传播不能完全纠正图中所有节点上的错误，因为它没有足够的 "总质量"，我们发现调整残差的比例在实践中会有很大帮助。为了做到这一点，我们提出了两种缩放残差的变化。

        自动缩放。直观地讲，我们希望将中的错误大小缩放为中的近似错误大小。我们只知道标记节点上的真实错误，所以我们用训练节点上的平均错误来近似缩放。正式地讲，让对应于的第行，并定义。然后通过给出未标记节点()上的校正预测。

        缩放固定的传播。另外，我们可以使用像Zhu等人（2003）的扩散，它保持训练节点的已知固定误差。更具体地说，从开始,我们迭代并且一直固定直到收敛。直观地说，这固定了我们知道误差的地方（在标记的节点上）的误差值，而其他节点一直在平均其邻居的数值，直到收敛。通过这种传播方式，中条目的最大值和最小值不会超过中的值。我们发现学习一个缩放超参数来产生是有效的。

3.3 用预测相关性来平滑最后的预测

        在这一点上，我们有一个分数向量，是用相关误差的模型对基础预测器进行修正得到的。为了做出最终的预测，我们进一步平滑校正后的预测。其动机是，图中的相邻节点很可能有类似的标签，鉴于网络的同质性或同构性，这是预期的。因此，我们可以通过另一个标签传播来鼓励标签分布的平滑性。首先，我们从我们对标签的最佳猜测开始:

(4)

        在这里，我们将训练节点设置为真实标签，并对验证集节点和无标签节点使用校正后的预测结果（我们也可以使用真实的验证标签，我们在后面的实验中讨论）。然后我们迭代，，直到收敛，得到最终预测值。一个节点的分类是。

        与误差相关一样，这里的平滑是一个后处理步骤，与其他步骤脱钩。这种类型的预测平滑在精神上与APPNP（Klicpera等人，2018）相似，我们在后面会对其进行比较。然而，APPNP是端到端的训练，在最终层表征上传播，而不是Softmaxes，不使用标签，而且动机不同。

3.4 总结和其他考虑

        为了回顾我们的通道，我们从一个廉价的基础预测开始，只使用节点特征而不使用图的结构。之后，我们通过传播训练数据上的已知错误来估计错误，从而得到错误修正的预测。最后，我们将其视为未标记节点的得分向量，并通过另一个LP步骤将其与已知标签结合起来，产生平滑的最终预测。我们把这个通道称为修正和平滑（C&S）。

        在展示这个通道在过渡性节点分类上取得最先进的性能之前，我们简要介绍另一种提高性能的简单方法：特征增强。深度学习的特点是，我们可以学习特征，而不是对它们进行工程设计。然而，GNN仍然依赖于信息量大的输入特征来进行预测。有许多方法可以从图的拓扑结构中获得有用的特征，以增强原始节点特征（Henderson等人，2011；2012；Hamilton等人，2017b）。在我们的通道中，我们用正则化频谱嵌入（Chaudhuri等，2012；Zhang & Rohe，2018）来增强特征，这些特征来自矩阵的前个特征向量，其中1是所有1的向量，是设置为平均程度的正则化参数，是对角线，其对角线项等于。底层矩阵是密集的，但是我们可以在与边的数量成线性关系的时间内应用矩阵-向量乘积，并使用迭代求解器来快速计算嵌入。

四、转导式节点分类实验

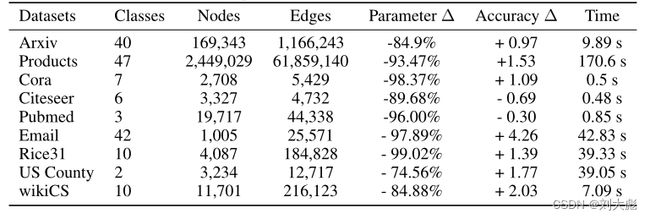
        为了证明我们方法的有效性，我们使用了九个数据集（表1）。Arxiv和Products数据集来自开放图谱基准（OGB）（Hu等人，2020）；Cora、Citeseer和Pubmed是三个经典的引文网络基准（Getoor等人，2001；Getoor，2005；Namata等人，2012）；而wikiCS是一个网络图谱（Mernyei & Cangea，2020）。在这些数据集中，类是论文、产品或网页的类别，而特征则来自文本。我们还使用了莱斯大学的Facebook社交网络，其中类是宿舍，特征是性别、专业和班级年级等属性（Traud等人，2012），以及美国各县的地理数据集，其中类是2016年选举结果，特征是人口统计学（Jia & Benson, 2020）。最后，我们使用了一个欧洲研究机构的电子邮件数据集，其中的类别是部门成员，没有任何特征（Leskovec等人，2007；Yin等人，2017）。

        表1：数据集的汇总统计。我们包括（i）参数数量的减少，（ii）与最先进的GNN方法相比，我们最好的C&S模型的准确性变化，以及（iii）训练时间。通过避免昂贵的GNN，我们的方法需要更少的参数，训练速度也更快。我们的方法通常更准确（另见表2和表4）。

        数据分割。Arxiv和产品的训练/验证/测试分割由基准给出，wikiCS的分割来自Mernyei & Cangea（2020）。对于Rice、美国各县和电子邮件数据，我们使用40%/10%/50%的随机分割，对于较小的引文网络，我们使用60%/20%/20%的随机分割，如Wang & Leskovec（2020）（与较低的标签率设置相反（Y ang等人，2016）），以改善对超参数的敏感性。在我们所有的实验中，预测准确率的标准偏差通常小于1%，不会改变我们的定性比较。

        基础预测器和其他模型。我们使用线性和MLP模型作为简单的基础预测器，其中输入特征是原始节点特征和光谱嵌入。我们还使用了一个只使用原始特征进行比较的普通线性模型和只使用标签传播（LP；特别是Zhou等人（2004）的版本）。对于可与我们的框架相比较的GNN模型（在简单性或风格方面），我们使用GCN、SGC和APPNP。对于GCN模型，我们增加了从输入到每一层以及从每一层到输出的额外剩余连接，这产生了更好的结果。GCNs的层数和隐藏通道的数量与MLPs相同。因此，这里的GCN代表一类GCN类型的模型，而不是原始模型Kipf & Welling（2017）。

        最后，我们包括几个 "最先进的"（SOTA）基线。对于Arxiv和产品，这是UniMP（Shi等人，2020）（截至2020年10月1日，OGB排行榜的第一名）。对于Cora、Citeseer和Pubmed，我们重新使用Chen等人（2020）的最高性能分数。对于Email和US County，我们使用GCNII（Chen et al, 2020）。对于Rice31，我们使用GCN与光谱和node2vec（Grover & Leskovec, 2016）嵌入（这是我们发现的最好的基于GNN的模型）。对于wikiCS，我们使用Mernyei & Cangea（2020）报告的APPNP。我们使用验证集来选择一组固定的超参数。更多的模型架构细节见附录。

4.1 节点分类的第一个结果

        在我们的第一组结果中，我们只使用C&S框架中的训练标签，因为这些是GNN通常用来训练模型的。对于这里讨论的结果，这对我们的基线来说是很慷慨的。包括验证标签的能力是我们的方法（以及一般的标签传播）的一个优势，这进一步提高了我们框架的性能（表1）。我们将在下一节讨论这个问题。

        表2报告了结果，我们强调了几个重要的发现。首先，在我们的模型中，LP的后处理步骤有很大的收益（例如，在产品上，MLP基础预测从63%上升到84%）。其次，即使是带有C&S的普通线性模型，在许多情况下也足以超过普通的GCNs，而LP（一种没有可学习参数的方法）往往与GCNs有相当的竞争力。考虑到GCNs的主要动机是解决连接的节点可能没有类似的标签这一事实，这一点很引人注目（Kipf & Welling, 2017）。我们的结果表明，直接将相关性纳入图中，简单地使用特征往往是一个更好的想法。第三，我们的模型变体可以在产品、Cora、电子邮件、Rice31和US County上的表现优于SOTA（通常是大幅优于）。在其他数据集上，我们表现最好的模型和SOTA之间没有太大的区别。

        表2：我们的C&S框架的性能，只使用方程（4）中的地面真实训练标签。通过包括地面真实验证标签（表4），可以做出进一步的改进。

        为了了解使用地面真实标签的直接帮助程度，我们还试验了一个没有标签的C&S版本。我们没有运行我们的LP步骤，而只是用Zhou等人（2004）的方法平滑基础预测器的输出，并将其称为基本模型。我们看到，线性和MLP基础预测器的性能往往可以超过GCN的性能（表3）。这些结果再次表明，平滑的输出是很重要的，而且GCN的原始动机是误导的。相反，我们假设GCN通过在图上有平滑的输出而获得性能，这是Wu等人（2019）的类似观察。然而，我们这里的模型与表2中直接使用标签的模型在性能上仍有差距。接下来，我们看看如何通过使用更多的标签来进一步提高C&S的性能。

未完，待更新。