opencv学习笔记十一：相机模型与标定（一：理论部分）

前言

我将这一部分分成两个部分来写，一个是理论部分，一个是具体实践部分。相机模型标定是我们抛去图像处理后接触的第一个比较“高级点”的东西，也是深入学习视觉其他东西的基础，比如做双目测距或者VO里程计。除此，相机标定也涉及一些好玩的数学方法，好好钻研一下也是很有好处和乐趣。

相机模型

我们高中都做过小孔成像的实验，小孔相机模型就是最简单通用的一种相机模型，这个模型我们就用下面一个图带过好了：

其中f为我们熟知的相机参数——焦距，而光轴与图像平面的角点称为主点。
实际中，主点并不是成像装置的中心，因为我们无法拿着镊子和胶水把相机里面的成像装置以微米级别精确安装，也没有必要。芯片的中心通常不在光轴上，这时我们就要引入两个新的参数Cx ， Cy（用来表示对投影屏幕坐标中心的偏移量），这样，物理世界中的点 Q ，其坐标为（X,Y,Z），根据下式投射到成像装置的摸个像素位置（Xscreen，Yscreen）:

注意，我们引入了两个不同的焦距 fx 和 fy ，原因时单个像素在低价成像装置上时矩形而不是正方形。
现在我们知道相机模型的基本结构和原理，就要考虑现实世界的点与相机成像的像素点坐标之间的关系了，我们将物理世界中坐标为（Xi，Yi，Zi）的点Qi 映射到投影平面上坐标为（xi，yi，zi）的点上的过程叫做 “ 射影变换 ”；
采用这种变换，可以方便的适应我们所熟知的齐次坐标把位数为n的投影空间的点用（n+1）维向量（例如x,y,z变为x,y,z,w）表示。其实我对齐次坐标并不熟悉。。所以查了一下，这是原文链接：https://blog.csdn.net/xiaoshen0121/article/details/79428678
因为感觉写的很好，就搬过来存上了//

对于一个向量v以及基oabc，可以找到一组坐标(v1,v2,v3)，使得v = v1 a + v2 b + v3 c （1）
而对于一个点p，则可以找到一组坐标（p1,p2,p3），使得 p – o = p1 a + p2 b + p3 c （2），
从上面对向量和点的表达，我们可以看出为了在坐标系中表示一个点（如p），我们把点的位置看作是对这个基的原点o所进行的一个位移，即一个向量——p – o（有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量），我们在表达这个向量的同时用等价的方式表达出了点p：p = o + p1 a + p2 b + p3 c (3)
(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出，虽然都是用代数分量的形式表达向量和点，但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7)，谁知道它是个向量还是个点！
我们现在把（1）（3）写成矩阵的形式：v = (v1 v2 v3 0) X (a b c o)
p = (p1 p2 p3 1) X (a b c o),这里(a,b,c,o)是坐标基矩阵，右边的列向量分别是向量v和点p在基下的坐标。这样，向量和点在同一个基下就有了不同的表达：3D向量的第4个代数分量是0，而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。
这样，上面的(1, 4, 7)如果写成（1,4,7,0），它就是个向量；如果是(1,4,7,1)，它就是个点。下面是如何在普通坐标(Ordinary Coordinate)和齐次坐标(Homogeneous Coordinate)之间进行转换：
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点，则变为(x,y,z,1);
如果(x,y,z)是个向量，则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1)，则知道它是个点，变成(x,y,z);
如果是(x,y,z,0)，则知道它是个向量，仍然变成(x,y,z)
以上是通过齐次坐标来区分向量和点的方式。从中可以思考得知，对于平移T、旋转R、缩放S这3个最常见的仿射变换，平移变换只对于点才有意义，因为普通向量没有位置概念，只有大小和方向.
而旋转和缩放对于向量和点都有意义，你可以用类似上面齐次表示来检测。从中可以看出，齐次坐标用于仿射变换非常方便。
此外，对于一个普通坐标的点P=(Px, Py, Pz)，有对应的一族齐次坐标(wPx, wPy, wPz, w)，其中w不等于零。比如，P(1, 4, 7)的齐次坐标有(1, 4, 7, 1)、（2, 8, 14, 2）、（-0.1, -0.4, -0.7, -0.1）等等。因此，如果把一个点从普通坐标变成齐次坐标，给x,y,z乘上同一个非零数w，然后增加第4个分量w；如果把一个齐次坐标转换成普通坐标，把前三个坐标同时除以第4个坐标，然后去掉第4个分量。
由于齐次坐标使用了4个分量来表达3D概念，使得平移变换可以使用矩阵进行，从而如F.S. Hill, JR所说，仿射（线性）变换的进行更加方便。由于图形硬件已经普遍地支持齐次坐标与矩阵乘法，因此更加促进了齐次坐标使用，使得它似乎成为图形学中的一个标准。
以上很好的阐释了齐次坐标的作用及运用齐次坐标的好处。其实在图形学的理论中，很多已经被封装的好的API也是很有研究的，要想成为一名专业的计算机图形学的学习者，除了知其然必须还得知其所以然。这样在遇到问题的时候才能迅速定位问题的根源，从而解决问题。

下面就是我们将物理世界的点投影到相机上的数学表示了：

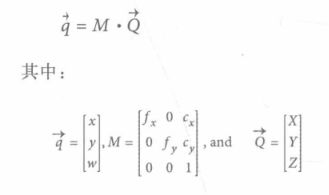
opencv中有专门的齐次坐标与非齐次坐标相互转换的函数：

	convertPointsToHomogeneous(
		InputArray	src,
		OutputArray	dst
	);

需要一个N维点的向量（用一般形式表示），并且从该向量中构造出（N+1）维点的向量。所有新构造的向量所添加的维度值设置为1。

	convertPointsFromHomogeneous(
		InputArray	src,
		OutputArray	dst
	);

从齐次坐标转换为普通坐标，给定N维点的输入向量，首先将每个点的所有分量除以改点的最后一个分量，再将最后一个分量丢弃，从而构造出（N-1）维点的向量。

至此，在将坐标系转换的过程中，我们共加了四个参数：Fx Fy Cx Cy , 他们所构成的矩阵M成为内参矩阵。

透镜畸变

我们知道了世界坐标与相机坐标之间的转换，但在针孔相机中，由于只有少量光线通过针孔，在实际中，无论使用何种图像采集器，都需要等待积累足够光线，因此成像速度非常慢。对于快速生成图像的相机而言，必须利用更大面积的光线，甚至让光线扭曲以达到让更多光线进来的目的。
我们使用透镜来达到这个目的，但自然也引入了畸变。
畸变分为径向畸变和切向畸变，径向畸变是由于透镜形状造成的，切向畸变是由于整个相机的组装过程造成的。

径向畸变

镜像畸变是有凸透镜本身形状引起的，好的透镜，经过一些精密处理，畸变并不明显，但在普通网络相机上畸变显得特别突出。我们可以把畸变看作r=0附近的泰勒奇数展开的前几项来便是。一般为前两项 k1 , k2，对于鱼眼透镜 ，会用前三项 k3 .
成像装置上某点的径向位置可以根据以下等式进行调整：

这里（x,y）是成像装置上畸变点的原始位置，（Xcorrected,Ycorrected）是矫正后的新位置。

切向畸变

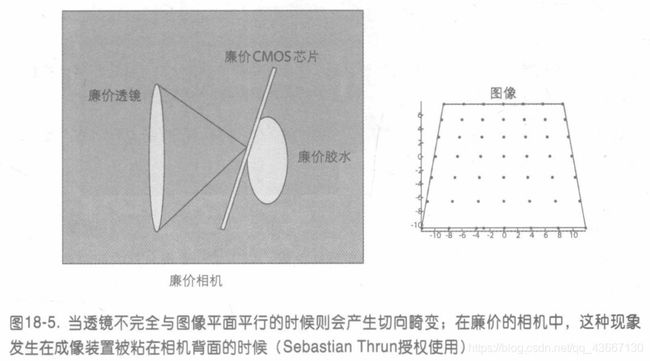
切向畸变是由于制造上的缺陷使透镜不与成像平面平行而产生的。切向畸变可以用两个参数p1 和 p2 来表示：

至此，我们得到了共五个参数：K1 K2 K3 P1 P2 ，这五个参数是我们消除畸变所必须的，称为畸变向量，也叫相机外参。

标定

首先，标定自然需要计算相机内参矩阵和畸变向量，opencv提供了函数cv::calibrateCamera（）函数来计算，在使用这个函数之前，我们先了解下标定板，最常用的标定板就是棋盘了，如下图：

棋盘要求精度需要很高，格子是正方形，买一张标定板很贵的，在csdn上下棋盘图也要画好多c币，即使给大家在这儿贴一张棋盘图，大家保存完也会有码，所以大家可以用word画一张，很简单的，只要做一个5*7的表格再涂色就可以了。
标定板有了，opencv为我们提供了一系列函数来计算畸变参数和外部参数，使用的方法是张正友标定法，但我们有matlab这么好用的工具软件，就不使用函数矫正了。因为电脑系统前段时间重装了，MATLAB还没下，标定过程以后再更新吧。

矫正函数应用

我们可以通过MATLAB来获取内参和畸变矩阵，接下来就是矫正了，opencv给我们提供了两种矫正方法，虽说是两种，但各有不同的特性和应用。在介绍这两个函数之前，先了解一下矫正映射。
在进行图像矫正时，我们必须指定输入图像中的每个像素在输出图像中移动的位置，称为“矫正映射”。这样的映射有三种表示方式：

1. 双通道浮点数表示，这种表示最为直接。NM图像的重映射由双通道浮点数NM矩阵表示，对与像素图像下标位置为（i,j）的点的值为（i0，j0）,（i0，j0）就表示该像素在矫正后的位置。
2. 双矩阵浮点表示，就是用两个单通道的矩阵N*M分别表示原像素点在矫正后的X坐标和Y坐标。
3. 定点表示。映射由双通道有符号整数矩阵表示，表示方法与双通道浮点数表示一样，但更快一些。
   opencv给我们提供了函数cv::convertMaps（）函数在不同表示方式之间转换矫正映射。
   下面，我们就要进行矫正了，我们有两种方法：
   方法一：
   使用cv::initUndistortRecitifyMap（）函数计算矫正映射，函数原型如下：

initUndistortRectifyMap(
	InputArray	cameraMaxtrix,    3*3内参矩阵 
	InputArray	distCoeffs,		  畸变系数1*4向量
	InputArray	R,				  可以使用或者设置为noArray()。是一个旋转矩阵，将在矫正前
							预先使用，来补偿相机相对于相机所处的全局坐标系的旋转。
	InputArray	newCameraMatrix,  单目成像时一般不会使用它
	Size		size,			  输出映射的尺寸，对应于用来矫正的图像的尺寸
	int			m1type,			  最终的映射类型，可能只为CV_32FC1  32_16SC2，对应于map1的表示类型
	OutputArray	map1,			  
	OutputArray	map2
);

我们只需在程序开头使用该函数计算一次矫正映射，就可以使用cv::remap（）函数将该矫正应用到视频每一帧图像。
方法二：
在某些情况下，我们只需要矫正一个图像，或者对一个图像重新计算矫正映射。这时候适应更加简洁的cv::undistort（）函数即可。

下面时一段矫正鱼眼摄像头的程序，相机内参和畸变参数已经有MATLAB求出：

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

const int imageWidth = 640; //图片大小    //摄像头的分辨率  
const int imageHeight = 480;
Size imageSize = Size(imageWidth, imageHeight);
Mat mapx, mapy;
// 相机内参
Mat cameraMatrix = (Mat_<double>(3, 3) << 273.4985, 0, 321.2298,
	0, 273.3338, 239.7912,
	0, 0, 1);
// 相机外参
Mat distCoeff = (Mat_<double>(1, 4) << -0.3551, 0.1386,0, 0);
Mat R = Mat::eye(3, 3, CV_32F);

VideoCapture cap1;

void img_init(void)
{
	//这初始化摄像头，但是我这种摄像头不知道是哪不好，设备号已经到700了而且必须关闭自带摄像头才能用
	int cont = -1;
	cap1.open(0);
	cap1.set(CAP_PROP_FOURCC, 'GPJM');
	cap1.set(CAP_PROP_FRAME_WIDTH, imageWidth);
	cap1.set(CAP_PROP_FRAME_HEIGHT, imageHeight);
}

int main()
{
	initUndistortRectifyMap(cameraMatrix, distCoeff, R, cameraMatrix, imageSize, CV_32FC1, mapx, mapy);
	Mat frame;
	img_init();

	while (1)
	{
		cap1>>frame;
		imshow("yuan",frame);
		remap(frame,frame,mapx,mapy, INTER_LINEAR);
		imshow("change",frame);
		waitKey(30);
	}
    return 0;
}

可以看到原本屏幕边缘是弧形的，矫正后是直的。