信号的分类

信号的分类

什么是信号？

信号是运载消息的工具，是消息的载体。从广义上讲，它包含光信号、声信号和电信号等。例如，古代人利用点燃烽火台而产生的滚滚狼烟，向远方军队传递敌人入侵的消息，这属于光信号；当我们说话时，声波传递到他人的耳朵，使他人了解我们的意图，这属于声信号；

基于信号维度的分类

一维信号：声音信号，声音强度随时间变化。

例如：下面这段声音信号，我们利用Matlab将这段信号的强度随时间变化的图像绘制出来。

WAV文件

clc
clear
folder='C:\Users\gzq62\Desktop\12_26.wav';%输入文件路径
[X, Fs] = audioread(folder);%读入音频
X = X(:,1);
%将音频数据从wav文件中读出
%X表示wav文件中的声音数据，Fs表示音频采样率（再wav文件头中有定义）   
T = 1/Fs;
t = (T*Fs : size(X))*T;
%将横坐标点数转换为时间%这里(T*Fs : size(y))是根据
%自己想要播放wav文件中哪个时间段自己修改
t = t';
X = 100*X(T* Fs : size(X)); %截取0秒到音频结束
plot(t,X);            %音频时域绘图
title("声音时域图");
xlabel("时间");
ylabel("幅值");
sound(X, Fs);          %播放音频

二维信号：图像信号，图像的横纵坐标的每个点用RGB编码，其中R、G、B个个分量用八位二进制表示，每个坐标点3*8位二进制数表示。

例如：将下面图片中每个像素点的RGB分量提取出来，图片的像素是1050*1680。

%读取一张图片，并显示
original_picture=imread('C:\Users\gzq62\Desktop\202212271737310.jpg');
subplot(2,2,1);
imshow(original_picture);
title('原始图像的直方图')

%分别读取R、G、B的值，1代表R，2代表G，3代表B
image_r=original_picture(:,:,1);
image_g=original_picture(:,:,2);
image_b=original_picture(:,:,3);
subplot(222)
imshow(image_r);
title('R  Part');

subplot(223)
imshow(image_g);
title('G  Part');

subplot(224)
imshow(image_b);
title('B  Part');

下表能更清晰的表示R分量在每个像素点的值。

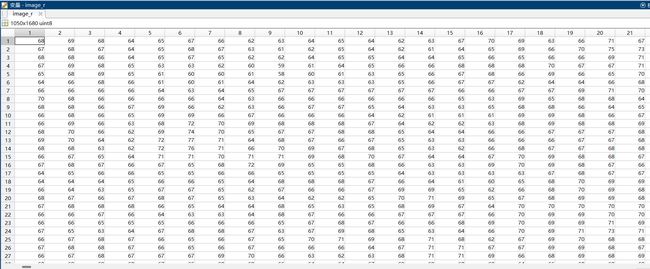
三维信号：电视的视频信号，在图像信号上加上一个时间轴，这里就不一一举例了。

确定性信号

任何可以被一个显式数学表达式、一个数据表或者一个定义好的规律所唯一描述的信号，称为确定性信号，确定性信号又包含周期信号和非周期信号。

周期信号：在（-∞，+∞）区间，每隔一定时间T（或整数N），按相同规律重复变化的信号。

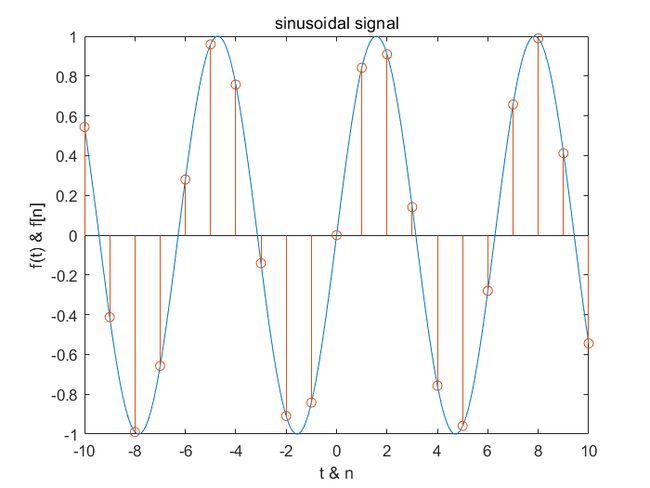
例如：正弦周期信号

t = -10:0.01:10; 
f1 = sin(t); 
plot(t,f1); 
hold on; 
n = -10 : 10;
f2 = sin(n);
stem(n, f2);

% 添加X轴、Y轴、标题
xlabel('t & n'); 
ylabel('f(t) & f[n]');
title('sinusoidal signal');

例如：复杂周期信号

t = -10:0.01:10; 
f1 = sin(t)+sin(2*t)+sin(3*t); 
plot(t,f1); 
hold on; 
n = -10 : 10;
f2 = sin(n)+sin(2*n)+sin(3*n);
stem(n, f2);

xlabel('t & n'); 
ylabel('f(t) & f[n]');
title('sinusoidal signal');

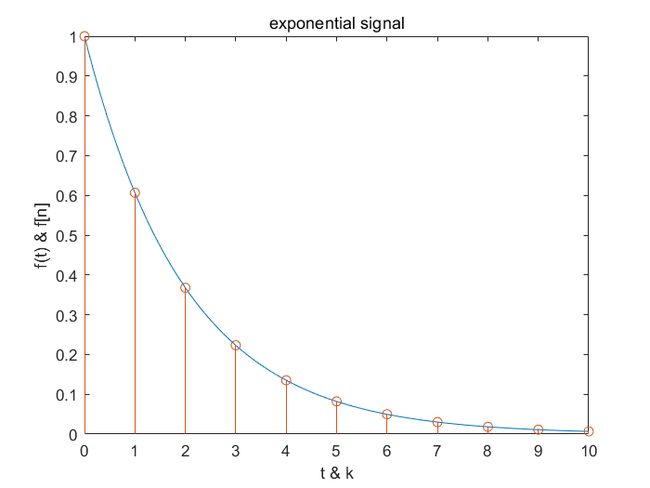
非周期信号：显然，非周期信号与上面周期性信号刚好相反

a = -0.5;
t = 0 : 0.01 : 10;
f1 = exp(a * t);
plot(t, f1);
hold on;
n = 0 : 10;
f2 = exp(a * n);
stem(n, f2);

xlabel('t & k');
ylabel('f(t) & f[n]');
title('exponential signal');

随机信号

信号不能用确切的函数描述，只可能知道它的统计特性比如概率，例如：电子系统中的起伏热噪声、雷电干扰信号。 (注意：随机信号是发生以后记录下来的，每一个时刻是什么值是不确定的）日常生活中，我们如果观察一个信号，当不知道任何关于这个信号的信息时，只能得到一个观测值。也就是说，在这种情况下，每隔几秒的采样结果只是我们对“信号”的观测，不能完全反应它的性质。

有了观测值，我们通常会把信号建模成一个随机变量。但是，信号通常都会随时间变化，如果随着时间流逝，能确定这个随机变量还服从同一个随机分布吗?它服从的分布特性不会变吗?

不能。比如极端一点，上一秒可能服从高斯分布，下一秒可能服从二项分布。因此，信号应当是一种随机过程。这就是平稳信号和非平稳信号的区别，平稳信号的统计参数不随时间变化，白噪声就是一个典型的平稳过程。

例如：平稳信号（指信号的分布参数或者分布律不随时间发生变化的信号，当你对他进行了一定时间的观测后，后续的观测就不需要了，因为已经获得了信号的全部统计信息了。）

clear,clc;
x=wgn(1,1001,2);
plot(x);

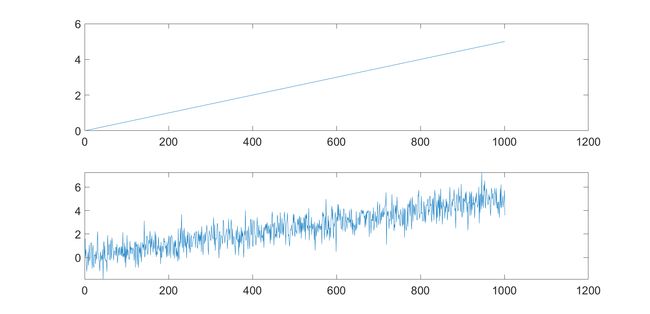
例如：非平稳信号（统计特性随时间在变，它的信息量是变化的。始终会有“新息”引入，在随机信号分析中，新息的定义就是当前信号值与预测信号值的差。预测信号是根据过去信号的统计特性推测出来的，也就是说新息是不可预测的部分。）

clear,clc;
i = 0.005.*(1:1:1001);
y=awgn(i,2);

subplot(2,1,1),plot(i);
subplot(2,1,2),plot(y);

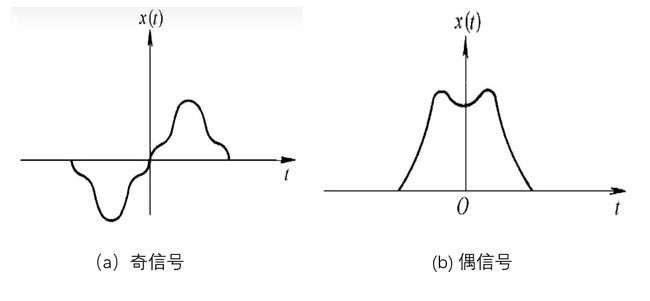
奇信号和偶信号

按信号是关于原点对称或关于纵坐标对称，又可以分为奇信号与偶信号。这点与我们学的奇函数与偶函数类似，在此不再赘述。

任何信号都能分解为两个信号之和，其中之一为偶信号，另一个为奇信号。

对于连续信号：
$$x\left(t\right)=\left[\frac{x\left(t\right)+x\left(-t\right)}{2}\right]+\left[\frac{x\left(t\right)-x\left(-t\right)}{2}\right]$$
对于离散信号：
$$x\left[n\right]=\left[\frac{x\left[n\right]+x\left[-n\right]}{2}\right]+\left[\frac{x\left[n\right]-x\left[-n\right]}{2}\right]$$
其中偶信号（even signal）为 $x_e\left(t\right)=\frac{x\left(t\right)+x\left(-t\right)}{2}$ 、奇信号（odd signal）为 $x_o\left(t\right)=\frac{x\left(t\right)-x\left(-t\right)}{2}$ 。信号的分解更利于我们后续的信号处理，分解为奇信号与偶信号利于我们利用奇偶性质进行处理。

能量信号和功率信号

对于一个信号f(t),其能量定义为：
$$E=\underset{T\to \infty }{\lim }{\int }_{-T}^T|f(t){|}^{2}dt$$
其功率定义为：
$$P=\underset{T\to \infty }{\lim }\frac{1}{2T}{\int }_{-T}^T|f(t){|}^{2}dt$$
由上式可见两种信号都是建立在时间无穷大的基础上的。

若函数E是一个有限值，则称该函数为能量有限信号。且由定义可知该信号功率→0；若函数E是一个无限值，则P有可能是有限值，也可能为无限值，但不会为0；若P为有限值，就称该信号为功率有限信号。一个信号不可能既是功率信号，又是能量信号，但可以既非功率信号，又非能量信号。

下面我们简单列举几个常见的信号分类：

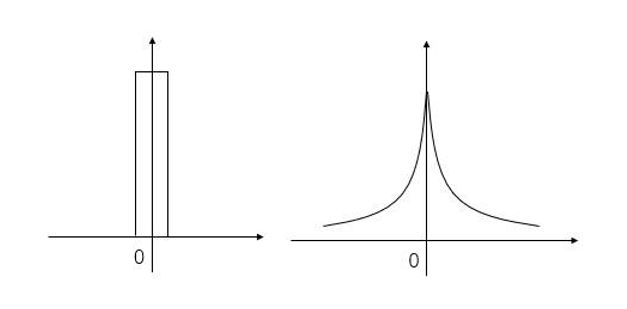
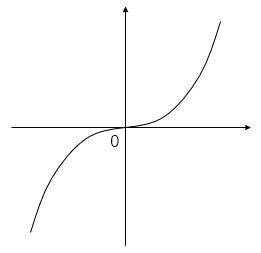
能量信号

功率信号

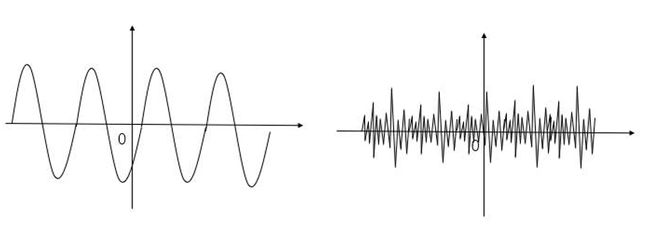
非能量非功率信号

附录：基本信号生成

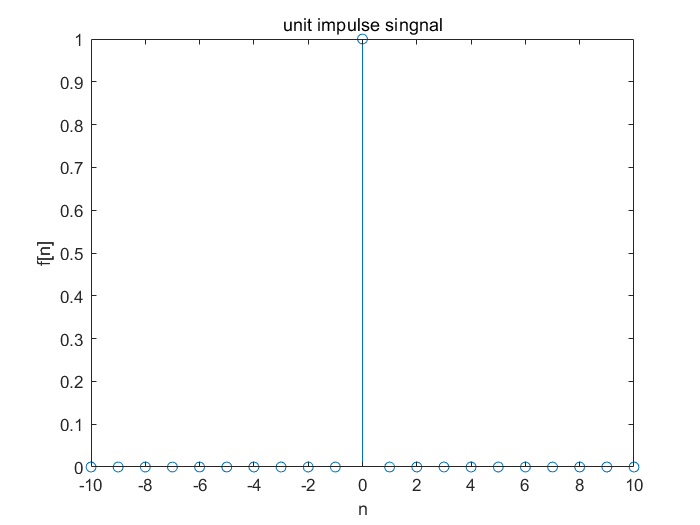
1. 单位冲激信号

数学公式

$$\delta [n]=\{\begin{array}{ll}0& n=0\\ 1& n\ne 0\end{array}$$

$$\{\begin{array}{l}\delta (t)=0;t\ne 0\\ {\int }_{-\infty }^{+\infty }\delta (t)\mathrm{d}t=1\end{array}$$

Matlab实现代码

n=-10:10;    %定义函数自变量取值范围
f1=(n==0);   %对f1赋值
stem(n,f1);  %绘制离散序列数据

% 添加X轴、Y轴、标题
xlabel('n'); 
ylabel('f[n]');
title('unit impulse singnal');

图形

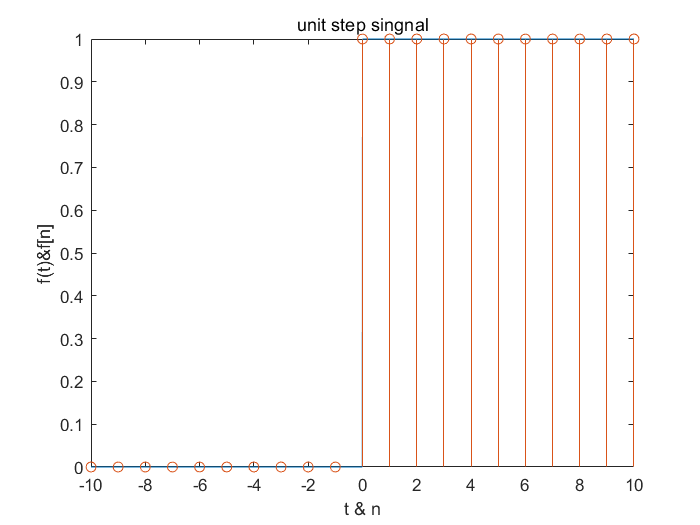
2. 单位阶跃信号

数学表达式

$$ϵ[n]=\{\begin{array}{ll}0& n<0\\ 1& n\ge 0\end{array}$$

$$ϵ(t)=\{\begin{array}{ll}0& t<0\\ 1& t\ge 0\end{array}$$

Matlab实现代码

t=-10:0.01:10;        %步长0.01，范围[-10,10]
f1=stepfun(t,0);    %阶跃函数
plot(t,f1);         %绘制连续曲线
hold on;            %使多条曲线在同一坐标轴上
n=-10:1:10;
f2=stepfun(n,0);
stem(n,f2);

% 添加X轴、Y轴、标题
xlabel('t & n');
ylabel('f(t)&f[n]');
title('unit step singnal');

图形

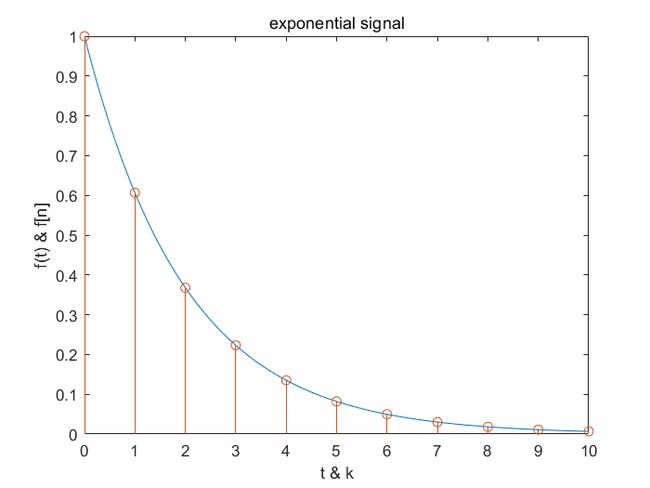
3. 指数信号

数学表达式

$$f(t)=A{e}^{\alpha t}$$

$$f[n]=A{e}^{\alpha n}$$

Matlab实现代码

a = -0.5;
t = 0 : 0.01 : 10;
f1 = exp(a * t);
plot(t, f1);
hold on;
n = 0 : 10;
f2 = exp(a * n);
stem(n, f2);

xlabel('t & k');
ylabel('f(t) & f[n]');
title('exponential signal');

图形

4. 矩形信号

数学表达式

$$g_{\tau }(t)=\{\begin{array}{ll}1& |t|<\frac{\tau }{2}\\ 0& |t|>\frac{\tau }{2}\end{array}$$

$$g_{\tau }[n]=\{\begin{array}{ll}1& |n|<\frac{\tau }{2}\\ 0& |n|>\frac{\tau }{2}\end{array}$$

Matlab实现代码

t = -1 : 0.01 : 1;       %rectpulse(t,w)可产生高度为1、宽度为w、
f1 = rectpuls(t,0.6);    %关于t=0对称的矩形脉冲信号，该函数的横坐标
plot(t, f1);             %范围由向量t决定，是以t=0为中心向左右扩展

hold on;

n = -1 :0.1: 1;
yd = rectpuls(n,0.6);
stem(n, yd);

xlabel('t & n');
ylabel('f(t) & f[n]');
title('rectangular signal');

图形

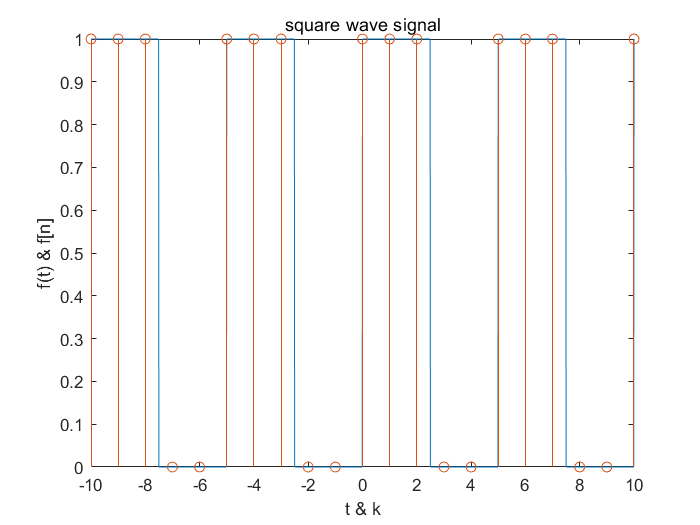
5. 方波信号

数学表达式

$$f(t)=\{\begin{array}{ll}1& kT\le t\le (kT+\frac{T}{2})\\ 0& (kT+\frac{T}{2})\le t\le (kT+T)\end{array}$$

$$f[n]=\{\begin{array}{ll}1& kT\le n\le (kT+\frac{T}{2})\\ 0& (kT+\frac{T}{2})\le n\le (kT+T)\end{array}$$

Matlab实现代码

t = -10 : 0.01 : 10;               %square函数用于产生周期性矩形脉冲信号
f1 = square(2*pi.*t/5, 50)/2+0.5;  %一般square调用形式为y=square(t,duty)
plot(t, f1);                       %duty指占空比

hold on;

n = -10 : 10;
f2 = square(2*pi.*n/5, 50)/2+0.5;
stem(n, f2);

xlabel('t & k');
ylabel('f(t) & f[n]');
title('square wave signal');

图形

6. 正弦信号

​ 因为余弦信号可以转换为正弦信号，所以这里统称为正弦信号。

$$f(t)=Asin(\omega t+\psi )$$

$$f[n]=Asin(\omega n+\psi )$$

Matlab实现代码

t = -10:0.01:10; 
f1 = sin(t); 
plot(t,f1); 
hold on; 
n = -10 : 10;
f2 = sin(n);
stem(n, f2);

% 添加X轴、Y轴、标题
xlabel('t & n'); 
ylabel('f(t) & f[n]');
title('sinusoidal signal');

图形

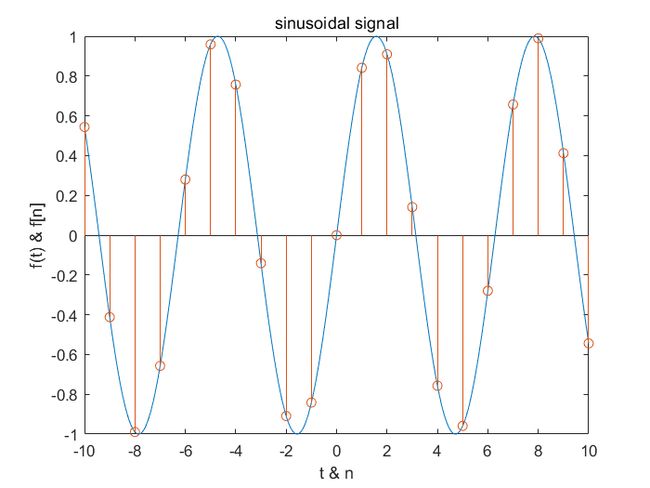
7. 抽样信号

数学表达式

$$S_a(t)=\frac{sin(t)}{t}$$

$$S_a[n]=\frac{sin(n)}{n}$$

性质
$${\int }_{-\infty }^{+\infty }\frac{sin(t)}{t}dt=\pi$$
Matlab实现代码

t = -10 : 0.01 : 10;
f1 = sinc(t / pi);
plot(t, f1);

hold on;

n= -10 : 10;
f2 = sinc(n / pi);
stem(n, f2);

xlabel('t & n');
ylabel('f(t) & f[n]');
title('sampling signal');

图形

8. 三角波&锯齿波信号

Matlab实现代码

t=0:0.001:1;             %sawtooth(t)为时间矢量t的元素生成周期为2π的锯齿波。
f1=sawtooth(2*pi*50*t);   %sawtooth(t,width)会生成一个修改后的三角波，
                            %其宽度（0和1之间的标量参数）决定最大值出现在0和2π之间的位置。
subplot(2,1,1);           %subplot（m,n,p)其中,m表示p个图排成m行，n表示图排成n列
plot(t,f1);
axis([0,0.2,-1,1]);
f2=sawtooth(2*pi*50*t,0.5);
subplot(2,1,2);
plot(t,f2)
axis([0,0.2,-1,1]);

图形

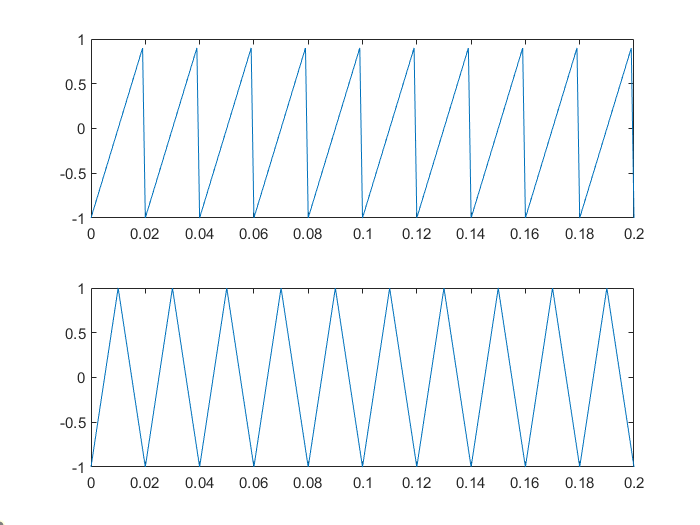
9. 随机信号

Matlab实现代码

n=1:1:60;
N=length(n);
f=rand(1 , N);
plot(t, f);
hold on;
stem(n , f);

xlabel('n');
ylabel('f(t)');
title('randon signal');

图形

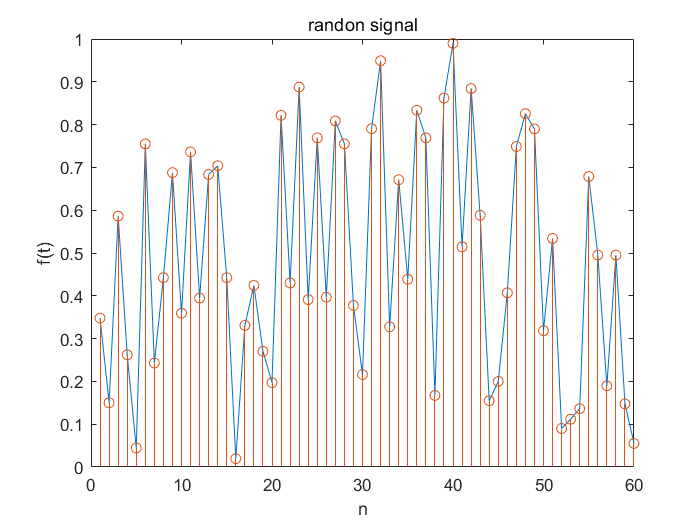
参考资料

信号（信息载体）_百度百科 (baidu.com)

典型的信号_哔哩哔哩_bilibili

随机信号_百度百科 (baidu.com)

(83 封私信) 什么是平稳信号和非平稳信号，怎么区别？ - 知乎 (zhihu.com)

(12条消息) 信号与系统——信号的分解_Xa_L的博客-CSDN博客_信号分解的偶分量和奇分量

能量信号和功率信号的分别 - 知乎 (zhihu.com)

(12条消息) 利用MATLAB实现基本信号的产生_希幕的博客-CSDN博客_如何用matlab产生信号

随机信号_百度百科 (baidu.com)

(83 封私信) 什么是平稳信号和非平稳信号，怎么区别？ - 知乎 (zhihu.com)

(12条消息) 信号与系统——信号的分解_Xa_L的博客-CSDN博客_信号分解的偶分量和奇分量

能量信号和功率信号的分别 - 知乎 (zhihu.com)

(12条消息) 利用MATLAB实现基本信号的产生_希幕的博客-CSDN博客_如何用matlab产生信号