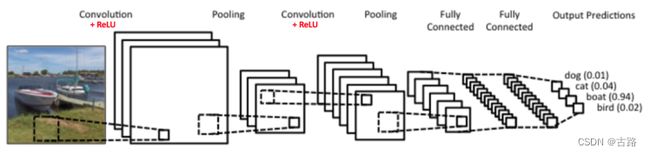
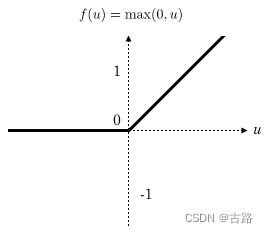
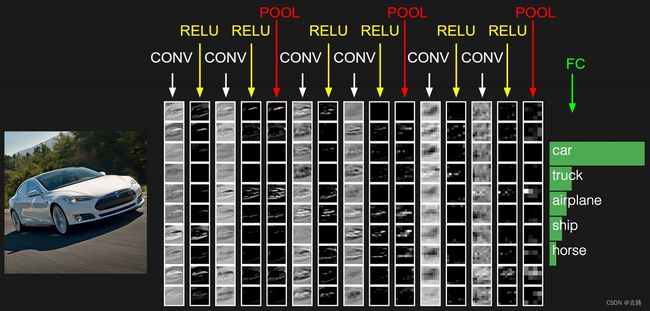
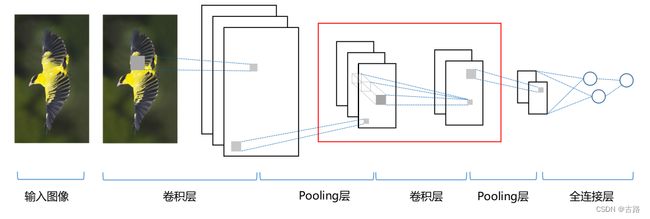
CNN神经网络
CNN神经网络
-
- 0.引言
-
- 0.1.卷积
- 0.2.Relu函数
- 0.3.池化pooling
- 0.4.小节
- 1.前向传播
-
- 1.1.input layer --> convolution layer
- 1.2.Hidden Layer --> convolution layer
- 1.3.Hidden layer --> pooling layer
- 1.4.Hidden layer --> full connected layer
- 1.5.小节
- 2.反向传播
-
- 2.1.pooling layer 的 δ l \delta ^l δl --> 上一 Hidden layer 的 δ l − 1 \delta ^{l-1} δl−1
-
- 2.1.1.max pooling
- 2.1.2.mean pooling
- 2.2.convolution layer 的 δ l \delta ^l δl --> 上一Hidden layer 的 δ l − 1 \delta ^{l-1} δl−1
-
- 2.2.1.最简单的情况: Step=1,Depth=1,Filter=1
- 2.2.2.步长为S的情况
- 2.2.3.深度为D时候
- 2.2.4.filter的数量为N的时候
- 2.2.5.N个filter,Depth为D
- 2.3.卷积层权重更新
0.引言
- 李宏毅老师的课件,用于感性理解很棒,理论推导还是得重来。
基础的就不赘述了。主要看推导。
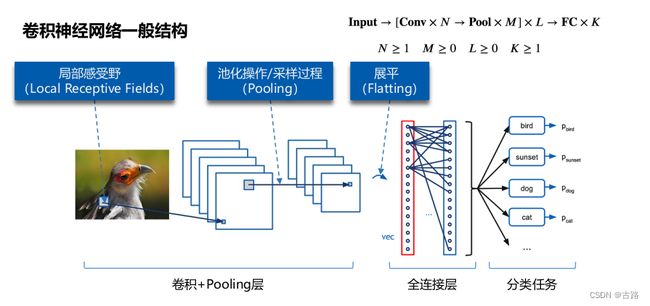
[convolution layer + Relu] --> pooling layer --> [convolution layer + Relu] --> pooling layer --> Fully Connected --> …
0.1.卷积
微积分中卷积的表达式为:
S ( t ) = ∫ x ( t − a ) w ( a ) d a S(t)=\int x(t-a) w(a) d a S(t)=∫x(t−a)w(a)da
离散形式是:
s ( t ) = ∑ a x ( t − a ) w ( a ) s(t)=\sum_a x(t-a) w(a) s(t)=a∑x(t−a)w(a)
矩阵表示为:
s ( t ) = ( X ∗ W ) ( t ) s(t)=(X * W)(t) s(t)=(X∗W)(t)
其中星号表示卷积。如果是二维的卷积, 则表示式为:
s ( i , j ) = ( X ∗ W ) ( i , j ) = ∑ m ∑ n x ( i − m , j − n ) w ( m , n ) s(i, j)=(X * W)(i, j)=\sum_m \sum_n x(i-m, j-n) w(m, n) s(i,j)=(X∗W)(i,j)=m∑n∑x(i−m,j−n)w(m,n)
在CNN中, 虽然说卷积, 但卷积公式和严格意义数学中的定义稍有不同,比如对于二维的卷积, 定义为:
s ( i , j ) = ( X ∗ W ) ( i , j ) = ∑ m ∑ n x ( i + m , j + n ) w ( m , n ) s(i, j)=(X * W)(i, j)=\sum_m \sum_n x(i+m, j+n) w(m, n) s(i,j)=(X∗W)(i,j)=m∑n∑x(i+m,j+n)w(m,n)
CNN的卷积都是指的后一个式子。其中,
- w w w 为卷积核,
- x x x 为输入。
如果 x x x 是一个二维输入的矩阵, 而 w w w 也是一个二维的矩阵。但是如果X是多维张量, 那么 W W W 也是多维张量。
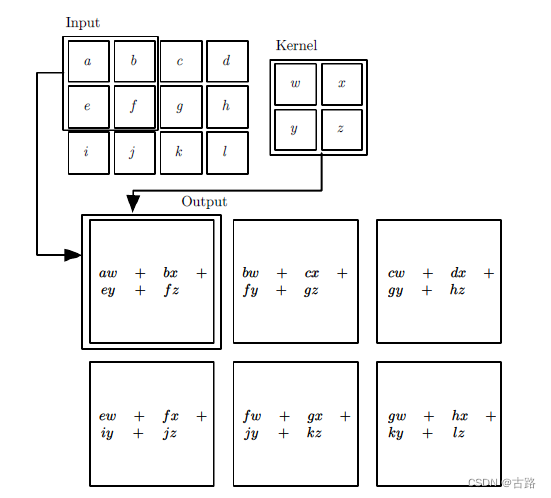
- 动态例子
0.2.Relu函数
0.3.池化pooling
- 参考博客
0.4.小节
卷积和池化操作都是降低数据维度,当然卷积根据旋转的filter的个数可能会是数据增加。再加上权值共享,都是简化网络的一些方法。
1.前向传播
一层一层理解。
1.1.input layer --> convolution layer
不管维度多高, 对于输入, 前向传播的过程可以表示为:
a 2 = σ ( z 2 ) = σ ( a 1 ∗ W 2 + b 2 ) a^2=\sigma\left(z^2\right)=\sigma\left(a^1 * W^2+b^2\right) a2=σ(z2)=σ(a1∗W2+b2)
其中,:
- 上标代表层数, 星号代表卷积,
- b代表我们的偏倚
- σ \sigma σ 为激活函数, 这里一般都是ReLU
CNN模型参数是:
- 1.一般卷积核不止一个, 比如有 K K K 个, 那么输入层的输出, 或者说第二层卷积层的对应的输入就 K K K 个;
- 2.卷积核中每个子矩阵的的大小, 一般都用子矩阵为方阵的卷积核, 比如 FxF的子矩阵;
- 3.填充padding (以下简称 P P P ), 卷积的时候, 为了可以更好的识别边缘, 一般都会在输入矩阵在周围加上若干圈的 0 再进行卷积, 加多少圈则 P P P 为多少;
- 4.步幅stride(以下简称 S \mathrm{S} S ), 即在卷积过程中每次移动的像素距离大小。
1.2.Hidden Layer --> convolution layer
普通隐藏层前向传播到卷积层时的前向传播算法。
假设隐藏层的输出是 M M M 个矩阵对应的三维张量, 则输出到卷积层的卷积核也是 M M M 个子矩阵对应的三维张量。这时表达式和输入层的很像, 也是
a l = σ ( z l ) = σ ( a l − 1 ∗ W l + b l ) a^l=\sigma\left(z^l\right)=\sigma\left(a^{l-1} * W^l+b^l\right) al=σ(zl)=σ(al−1∗Wl+bl)
也可以写成 M M M 个矩阵子矩阵卷积后对应位置相加的形式,即:
a l = σ ( z l ) = σ ( ∑ k = 1 M z k l ) = σ ( ∑ k = 1 M a k l − 1 ∗ W k l + b l ) a^l=\sigma\left(z^l\right)=\sigma\left(\sum_{k=1}^M z_k^l\right)=\sigma\left(\sum_{k=1}^M a_k^{l-1} * W_k^l+b^l\right) al=σ(zl)=σ(k=1∑Mzkl)=σ(k=1∑Makl−1∗Wkl+bl)
和上一节唯一的区别仅仅在于, 这里的输入是隐藏层来的, 而不是输入的原始图片样本形成的矩阵。
需要定义的CNN模型参数也和上一节一样,这里需要定义卷积核的个数K,卷积核子矩阵的维度 F, 填充大小P以及步幅S。
1.3.Hidden layer --> pooling layer
池化层的处理逻辑是比较简单的, 对输入的矩阵进行缩小概括。比如输入的若干矩阵是 N x N N x N NxN 维的, 而池化大小是 k x k k x k kxk 的区域, 则输 出的矩阵都是 N k × N k \frac{N}{k} \times \frac{N}{k} kN×kN 维的。
这里需要需要定义的CNN模型参数是:
- 1)池化区域的大小k
- 2)池化的标准, 一般是MAX或者Average
1.4.Hidden layer --> full connected layer
由于全连接层就是普通的模型结构, 即:
a l = σ ( z l ) = σ ( W l a l − 1 + b l ) a^l=\sigma\left(z^l\right)=\sigma\left(W^l a^{l-1}+b^l\right) al=σ(zl)=σ(Wlal−1+bl)
这里的激活函数一般是sigmoid或者tanh.
经过了若干全连接层之后,最后的一层为Softmax输出层。此时输出层和普通的全连接层唯一的区别是,激活函数是softmax函数。
这里需要需要定义的CNN模型参数是:
- 1)全连接层的激活函数
- 2)全连接层各层神经元的个数
1.5.小节
2.反向传播
类比 BP 的反向传播算法:
但是也有一些不同的地方:
- 1.池化层没有激活函数, 这个问题倒比较好解决, 可以令池化层的激活函数为 σ ( z ) = z \sigma(z)=z σ(z)=z, 即激活后就是自己本身。这样池化层激活函数的导数为1.
- 2.池化层在前向传播的时候, 对输入进行了压缩, 那么现在需要向前反向推导 δ l − 1 \delta^{l-1} δl−1, 这个推导方法和BP完全不同。
- 3.卷积层是通过张量卷积, 或者说若干个矩阵卷积求和而得的当前层的输出, 这和BP不相同, BP的全连接层是直接进行矩阵乘法得到当前层的输出。这样在卷积层反向传播的时候, 上一层的 δ l − 1 \delta^{l-1} δl−1 递推计算方法肯定有所不同。
- 4.对于卷积层, 由于 W W W 使用的运算是卷积, 那么从 δ l \delta^l δl 推导出该层的所有卷积核的 W , b W, b W,b 的方式也不同。
从上面可以看出, 问题1比较好解决, 但问题 2 , 3 , 4 2,3,4 2,3,4 就是解决CNN反向传播算法的关键所在了。
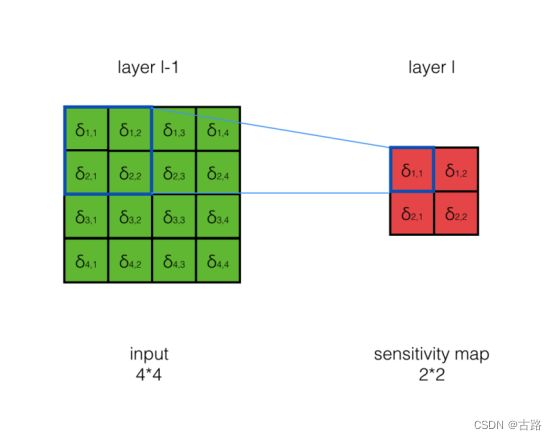
2.1.pooling layer 的 δ l \delta ^l δl --> 上一 Hidden layer 的 δ l − 1 \delta ^{l-1} δl−1
无论max pooling还是mean pooling,都没有需要学习的参数。因此,在卷积神经网络的训练中,Pooling层需要做的仅仅是将误差项传递到上一层,而没有梯度的计算。
在前向传播算法时, 池化层一般会用max pooling或者mean pooling对输入进行池化, 池化的区域大小已知。现在反过来, 要从缩小后的误差 δ l \delta^l δl, 还原前一 次较大区域对应的误差。
在反向传播时, 首先会把 δ l \delta^l δl 的所有子矩阵矩阵大小还原成池化之前的大小,:
- max pooling, 把 δ l \delta^l δl 的所有子矩阵的各个池化局域的值放在之前做 前向传播算法得到最大值的位置。
- mean pooling, 把 δ l \delta^l δl 的所有子矩阵的各个池化局域的值取平均后放在还原后的子矩阵位置。
这个过程一般叫做upsample上采样。
用一个例子可以很方便的表示: 假设池化区域大小是 2 × 2 2 \times 2 2×2 。 δ l \delta^l δl 的第 k \mathrm{k} k 个子矩阵为:
δ k l = ( 2 8 4 6 ) \delta_k^l=\left(\begin{array}{ll} 2 & 8 \\ 4 & 6 \end{array}\right) δkl=(2486)
由于池化区域为 2 × 2 2 \times 2 2×2, 此时先将 δ k l \delta_k^l δkl 做还原, 即变成:
( 0 0 0 0 0 2 8 0 0 4 6 0 0 0 0 0 ) \left(\begin{array}{llll} 0 & 0 & 0 & 0 \\ 0 & 2 & 8 & 0 \\ 0 & 4 & 6 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) 0000024008600000
如果是 max pooling, 假设之前在前向传播时记录的最大值位置分别是左上, 右下, 右上, 左下, 则转换后的矩阵为:
( 2 0 0 0 0 0 0 8 0 4 0 0 0 0 6 0 ) \left(\begin{array}{llll} 2 & 0 & 0 & 0 \\ 0 & 0 & 0 & 8 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 6 & 0 \end{array}\right) 2000004000060800
如果是mean pooling, 则进行平均: 转换后的矩阵为:
( 0.5 0.5 2 2 0.5 0.5 2 2 1 1 1.5 1.5 1 1 1.5 1.5 ) \left(\begin{array}{cccc} 0.5 & 0.5 & 2 & 2 \\ 0.5 & 0.5 & 2 & 2 \\ 1 & 1 & 1.5 & 1.5 \\ 1 & 1 & 1.5 & 1.5 \end{array}\right) 0.50.5110.50.511221.51.5221.51.5
这样就得到了上一层 ∂ J ( W , b ) ∂ a k l − 1 \frac{\partial J(W, b)}{\partial a_k^{l-1}} ∂akl−1∂J(W,b) 的值, 要得到 δ k l − 1 \delta_k^{l-1} δkl−1 :
δ k l − 1 = ( ∂ a k l − 1 ∂ z k l − 1 ) T ∂ J ( W , b ) ∂ a k l − 1 = upsample ( δ k l ) ⊙ σ ′ ( z k l − 1 ) \delta_k^{l-1}=\left(\frac{\partial a_k^{l-1}}{\partial z_k^{l-1}}\right)^T \frac{\partial J(W, b)}{\partial a_k^{l-1}}=\text { upsample }\left(\delta_k^l\right) \odot \sigma^{\prime}\left(z_k^{l-1}\right) δkl−1=(∂zkl−1∂akl−1)T∂akl−1∂J(W,b)= upsample (δkl)⊙σ′(zkl−1)
其中, upsample函数完成了池化误差矩阵放大与误差重新分配的逻辑。
概括下, 对于张量 δ l − 1 \delta^{l-1} δl−1, 有:
δ l − 1 = upsample ( δ l ) ⊙ σ ′ ( z l − 1 ) \delta^{l-1}=\text { upsample }\left(\delta^l\right) \odot \sigma^{\prime}\left(z^{l-1}\right) δl−1= upsample (δl)⊙σ′(zl−1)
2.1.1.max pooling
max pooling 前向传播: n e t 1 , 1 l = max ( net 1 , 1 l − 1 , net 1 , 2 l − 1 net_{1,1}^l=\max \left(\operatorname{net}_{1,1}^{l-1}, \operatorname{net}_{1,2}^{l-1}\right. net1,1l=max(net1,1l−1,net1,2l−1, net 2 , 1 l − 1 , net 2 , 2 l − 1 ) \left._{2,1}^{l-1}, \operatorname{net}_{2,2}^{l-1}\right) 2,1l−1,net2,2l−1)
上图中的
∂ n e t 1 , 1 l ∂ n e t 1 , 1 l − 1 = 1 \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,1}^{l-1}}=1 ∂net1,1l−1∂net1,1l=1
∂ n e t 1 , 1 l ∂ n e t 1 , 2 l − 1 = 0 \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,2}^{l-1}}=0 ∂net1,2l−1∂net1,1l=0
∂ n e t 1 , 1 l ∂ n e t 2 , 1 l − 1 = 0 \frac{\partial n e t_{1,1}^l}{\partial n e t_{2,1}^{l-1}}=0 ∂net2,1l−1∂net1,1l=0
∂ n e t 1 , 1 l ∂ net t 2 , 2 l − 1 = 0 \frac{\partial n e t_{1,1}^l}{\partial \text { net } t_{2,2}^{l-1}}=0 ∂ net t2,2l−1∂net1,1l=0
δ 1 , 1 l − 1 = ∂ E d ∂ net 1 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l − 1 = δ 1 , 1 l \quad \delta_{1,1}^{l-1}=\frac{\partial E_d}{\partial \text { net }_{1,1}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,1}^{l-1}} =\delta_{1,1}^l δ1,1l−1=∂ net 1,1l−1∂Ed=∂net1,1l∂Ed∂net1,1l−1∂net1,1l=δ1,1l
δ 1 , 2 l − 1 = ∂ E d ∂ net 1 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 1 , 2 l − 1 = 0 \quad \delta_{1,2}^{l-1}=\frac{\partial E_d}{\partial \text { net }_{1,2}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,2}^{l-1}} =0 δ1,2l−1=∂ net 1,2l−1∂Ed=∂net1,1l∂Ed∂net1,2l−1∂net1,1l=0
δ 2 , 1 l − 1 = ∂ E d ∂ net 2 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 2 , 1 l − 1 = 0 \quad \delta_{2,1}^{l-1}=\frac{\partial E_d}{\partial \text { net }_{2,1}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{2,1}^{l-1}} =0 δ2,1l−1=∂ net 2,1l−1∂Ed=∂net1,1l∂Ed∂net2,1l−1∂net1,1l=0
δ 2 , 2 l − 1 = ∂ E d ∂ net 2 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 2 , 2 l − 1 = 0 \quad \delta_{2,2}^{l-1}=\frac{\partial E_d}{\partial \text { net }_{2,2}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{2,2}^{l-1}} =0 δ2,2l−1=∂ net 2,2l−1∂Ed=∂net1,1l∂Ed∂net2,2l−1∂net1,1l=0
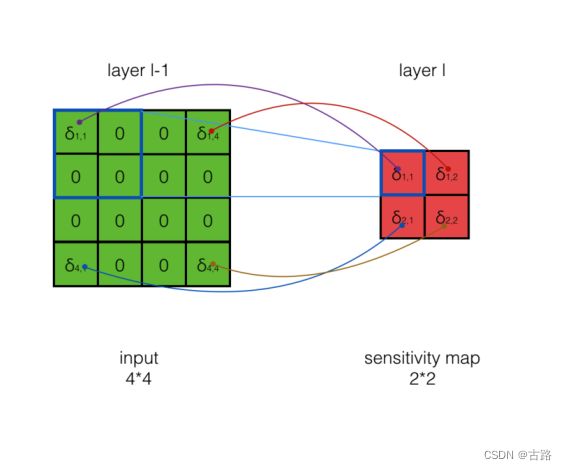
对于max pooling,下一层的误差项的值会原封不动地传递到上一层对应区块中的最大值所对应的 神经元,而其他神经元的误差项的值都是 0 。
如上图所示, layer l l l 层的误差 δ 1 , 1 \delta_{1,1} δ1,1 会原封不动地传递到layer l − 1 l-1 l−1 层对应区块 ( δ 1 , 1 δ 1 , 2 δ 2 , 1 δ 2 , 2 ) \left(\begin{array}{cc}\delta_{1,1} & \delta_{1,2} \\ \delta_{2,1} & \delta_{2,2}\end{array}\right) (δ1,1δ2,1δ1,2δ2,2) 中的最大值 所对应的神经元。
2.1.2.mean pooling
mean pooling前向传播: n e t 1 , 1 l = 1 4 ( n e t 1 , 1 l − 1 + n e t 1 , 2 l − 1 + n e t 2 , 1 l − 1 + n e t 2 , 2 l − 1 ) net_{1,1}^l=\frac{1}{4}\left(n e t_{1,1}^{l-1}+n e t_{1,2}^{l-1}+n e t_{2,1}^{l-1}+n e t_{2,2}^{l-1}\right) net1,1l=41(net1,1l−1+net1,2l−1+net2,1l−1+net2,2l−1)
$ \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,1}^{l-1}}=\frac{1}{4}$
∂ n e t 1 , 1 l ∂ n e t 1 , 2 l − 1 = 1 4 \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,2}^{l-1}}=\frac{1}{4} ∂net1,2l−1∂net1,1l=41
∂ net t 1 , 1 l ∂ net 2 , 1 l − 1 = 1 4 \frac{\partial \text { net } t_{1,1}^l}{\partial \text { net }_{2,1}^{l-1}}=\frac{1}{4} ∂ net 2,1l−1∂ net t1,1l=41
∂ n e t 1 , 1 l ∂ net t 2 , 2 l − 1 = 1 4 \frac{\partial n e t_{1,1}^l}{\partial \text { net } t_{2,2}^{l-1}}=\frac{1}{4} ∂ net t2,2l−1∂net1,1l=41
δ 1 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l − 1 = 1 4 δ 1 , 1 l \quad \delta_{1,1}^{l-1}=\frac{\partial E_d}{\partial n e t_{1,1}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,1}^{l-1}} \quad=\frac{1}{4} \delta_{1,1}^l δ1,1l−1=∂net1,1l−1∂Ed=∂net1,1l∂Ed∂net1,1l−1∂net1,1l=41δ1,1l
δ 1 , 2 l − 1 = ∂ E d ∂ n e t 1 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 1 , 2 l − 1 = 1 4 δ 1 , 1 l \quad \delta_{1,2}^{l-1}=\frac{\partial E_d}{\partial n e t_{1,2}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{1,2}^{l-1}} \quad=\frac{1}{4} \delta_{1,1}^l δ1,2l−1=∂net1,2l−1∂Ed=∂net1,1l∂Ed∂net1,2l−1∂net1,1l=41δ1,1l
δ 2 , 1 l − 1 = ∂ E d ∂ n e t 2 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 2 , 1 l − 1 = 1 4 δ 1 , 1 l \quad \delta_{2,1}^{l-1}=\frac{\partial E_d}{\partial n e t_{2,1}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{2,1}^{l-1}} \quad=\frac{1}{4} \delta_{1,1}^l δ2,1l−1=∂net2,1l−1∂Ed=∂net1,1l∂Ed∂net2,1l−1∂net1,1l=41δ1,1l
δ 2 , 2 l − 1 = ∂ E d ∂ n e t 2 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ n e t 2 , 2 l − 1 = 1 4 δ 1 , 1 l \quad \delta_{2,2}^{l-1}=\frac{\partial E_d}{\partial n e t_{2,2}^{l-1}} \quad=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial n e t_{2,2}^{l-1}} \quad=\frac{1}{4} \delta_{1,1}^l δ2,2l−1=∂net2,2l−1∂Ed=∂net1,1l∂Ed∂net2,2l−1∂net1,1l=41δ1,1l
对于mean pooling,下一层的误差项的值会平均分配到上一层对应区块中的所有神经元。 如上图所示, layer l l l 层的误差 δ 1 , 1 \delta_{1,1} δ1,1 会平均分配到layer l − 1 l-1 l−1 层对应区块 ( δ 1 , 1 δ 1 , 2 δ 2 , 1 δ 2 , 2 ) \left(\begin{array}{ll}\delta_{1,1} & \delta_{1,2} \\ \delta_{2,1} & \delta_{2,2}\end{array}\right) (δ1,1δ2,1δ1,2δ2,2) 中的所有神经元。
2.2.convolution layer 的 δ l \delta ^l δl --> 上一Hidden layer 的 δ l − 1 \delta ^{l-1} δl−1
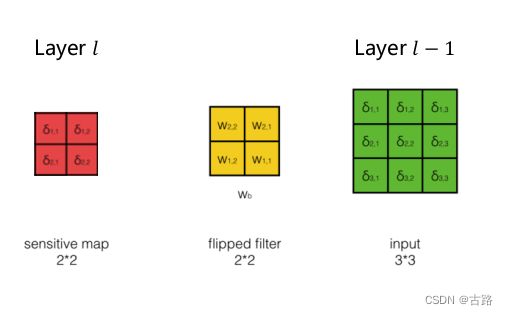
2.2.1.最简单的情况: Step=1,Depth=1,Filter=1
整体思想:
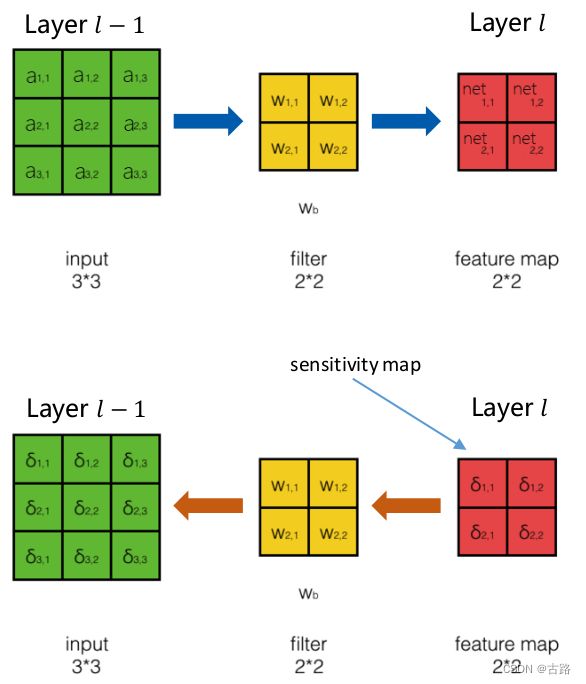
前向传播:
a i , j l − 1 = f l − 1 ( n e t i , j l − 1 ) n e t l = conv ( W l , a l − 1 ) + w b \begin{aligned} & a_{i, j}^{l-1}=f^{l-1}\left(ne t_{i, j}^{l-1}\right) \\ & net^l=\operatorname{conv}\left(W^l, a^{l-1}\right)+w_b \end{aligned} ai,jl−1=fl−1(neti,jl−1)netl=conv(Wl,al−1)+wb
误差后向传播:
δ i , j l − 1 = ∂ E d ∂ net i , j l − 1 = ∂ E d ∂ a i , j l − 1 ∂ a i , j l − 1 ∂ n e t i , j I − 1 \delta_{i, j}^{l-1}=\frac{\partial E_d}{\partial \text { net }_{i, j}^{l-1}}=\frac{\partial E_d}{\partial a_{i, j}^{l-1}} \frac{\partial a_{i, j}^{l-1}}{\partial n e t_{i, j}^{I-1}} δi,jl−1=∂ net i,jl−1∂Ed=∂ai,jl−1∂Ed∂neti,jI−1∂ai,jl−1
前向计算:
n e t 1 , 1 l = w 1 , 1 a 1 , 1 l − 1 + w 1 , 2 a 1 , 2 l − 1 + w 2 , 1 a 2 , 1 l − 1 + w 2 , 2 a 2 , 2 l − 1 + w b (1) n e t_{1,1}^l=w_{1,1} a_{1,1}^{l-1}+w_{1,2} a_{1,2}^{l-1}+w_{2,1} a_{2,1}^{l-1}+w_{2,2} a_{2,2}^{l-1}+w_b \tag{1} net1,1l=w1,1a1,1l−1+w1,2a1,2l−1+w2,1a2,1l−1+w2,2a2,2l−1+wb(1) n e t 1 , 2 l = w 1 , 1 a 1 , 2 l − 1 + w 1 , 2 a 1 , 3 l − 1 + w 2 , 1 a 2 , 2 l − 1 + w 2 , 2 a 2 , 3 l − 1 + w b (2) n e t_{1,2}^l=w_{1,1} a_{1,2}^{l-1}+w_{1,2} a_{1,3}^{l-1}+w_{2,1} a_{2,2}^{l-1}+w_{2,2} a_{2,3}^{l-1}+w_b \tag{2} net1,2l=w1,1a1,2l−1+w1,2a1,3l−1+w2,1a2,2l−1+w2,2a2,3l−1+wb(2) n e t 2 , 1 l = w 1 , 1 a 2 , 1 l − 1 + w 1 , 2 a 2 , 2 l − 1 + w 2 , 1 a 3 , 1 l − 1 + w 2 , 2 a 3 , 2 l − 1 + w b (3) n e t_{2,1}^l=w_{1,1} a_{2,1}^{l-1}+w_{1,2} a_{2,2}^{l-1}+w_{2,1} a_{3,1}^{l-1}+w_{2,2} a_{3,2}^{l-1}+w_b \tag{3} net2,1l=w1,1a2,1l−1+w1,2a2,2l−1+w2,1a3,1l−1+w2,2a3,2l−1+wb(3) n e t 2 , 2 l = w 1 , 1 a 2 , 2 l − 1 + w 1 , 2 a 2 , 3 l − 1 + w 2 , 1 a 3 , 2 l − 1 + w 2 , 2 a 3 , 3 l − 1 + w b (4) n e t_{2,2}^l=w_{1,1} a_{2,2}^{l-1}+w_{1,2} a_{2,3}^{l-1}+w_{2,1} a_{3,2}^{l-1}+w_{2,2} a_{3,3}^{l-1}+w_b \tag{4} net2,2l=w1,1a2,2l−1+w1,2a2,3l−1+w2,1a3,2l−1+w2,2a3,3l−1+wb(4)
误差后向传播:
∂ E d ∂ a 1 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ a 1 , 1 l − 1 = δ 1 , 1 l w 1 , 1 \begin{aligned} \frac{\partial E_d}{\partial a_{1,1}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial a_{1,1}^{l-1}} =\delta_{1,1}^l w_{1,1} \end{aligned} ∂a1,1l−1∂Ed=∂net1,1l∂Ed∂a1,1l−1∂net1,1l=δ1,1lw1,1
∂ E d ∂ a 1 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ a 1 , 2 l − 1 + ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ a 1 , 2 l − 1 = δ 1 , 1 l w 1 , 2 + δ 1 , 2 l w 1 , 1 \begin{aligned} \frac{\partial E_d}{\partial a_{1,2}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial a_{1,2}^{l-1}}+\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial n e t_{1,2}^l}{\partial a_{1,2}^{l-1}} =\delta_{1,1}^l w_{1,2}+\delta_{1,2}^l w_{1,1} \end{aligned} ∂a1,2l−1∂Ed=∂net1,1l∂Ed∂a1,2l−1∂net1,1l+∂net1,2l∂Ed∂a1,2l−1∂net1,2l=δ1,1lw1,2+δ1,2lw1,1
∂ E d ∂ a 1 , 3 l − 1 = ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ a 1 , 3 l − 1 = δ 1 , 2 l w 1 , 2 \begin{aligned} \frac{\partial E_d}{\partial a_{1,3}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial n e t_{1,2}^l}{\partial a_{1,3}^{l-1}} =\delta_{1,2}^l w_{1,2}\end{aligned} ∂a1,3l−1∂Ed=∂net1,2l∂Ed∂a1,3l−1∂net1,2l=δ1,2lw1,2
∂ E d ∂ a 2 , 1 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ a 2 , 1 l − 1 + ∂ E d ∂ n e t 2 , 1 l ∂ n e t 2 , 1 l ∂ a 2 , 1 l − 1 = δ 1 , 1 l w 2 , 1 + δ 2 , 1 l w 1 , 1 \begin{aligned} \frac{\partial E_d}{\partial a_{2,1}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial a_{2,1}^{l-1}}+\frac{\partial E_d}{\partial n e t_{2,1}^l} \frac{\partial n e t_{2,1}^l}{\partial a_{2,1}^{l-1}} =\delta_{1,1}^l w_{2,1}+\delta_{2,1}^l w_{1,1}\end{aligned} ∂a2,1l−1∂Ed=∂net1,1l∂Ed∂a2,1l−1∂net1,1l+∂net2,1l∂Ed∂a2,1l−1∂net2,1l=δ1,1lw2,1+δ2,1lw1,1
∂ E d ∂ a 2 , 2 l − 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ a 2 , 2 l − 1 + ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ a 2 , 2 l − 1 + ∂ E d ∂ n e t 2 , 1 l ∂ n e t 2 , 1 ∂ a 2 , 2 l − 1 + ∂ E d ∂ n e t 2 , 2 l ∂ n e t 2 , 2 l ∂ a 2 , 2 l − 1 = δ 1 , 1 l w 2 , 2 + δ 1 , 2 l w 2 , 1 + δ 2 , 1 l w 1 , 2 + δ 2 , 2 l w 1 , 1 \frac{\partial E_d}{\partial a_{2,2}^{l-1}} =\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial ne t_{1,1}^l}{\partial a_{2,2}^{l-1}}+\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial ne t_{1,2}^l}{\partial a_{2,2}^{l-1}}+\frac{\partial E_d}{\partial n e t_{2,1}^l} \frac{ \partial { net }_{2,1}}{\partial a_{2,2}^{l-1}}+\frac{\partial E_d}{\partial { net }_{2,2}^l} \frac{\partial { net }_{2,2}^l}{\partial a_{2,2}^{l-1}}=\delta_{1,1}^l w_{2,2}+\delta_{1,2}^l w_{2,1}+\delta_{2,1}^l w_{1,2}+\delta_{2,2}^l w_{1,1} ∂a2,2l−1∂Ed=∂net1,1l∂Ed∂a2,2l−1∂net1,1l+∂net1,2l∂Ed∂a2,2l−1∂net1,2l+∂net2,1l∂Ed∂a2,2l−1∂net2,1+∂net2,2l∂Ed∂a2,2l−1∂net2,2l=δ1,1lw2,2+δ1,2lw2,1+δ2,1lw1,2+δ2,2lw1,1
∂ E d ∂ a 2 , 3 l − 1 = ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ a 2 , 3 l − 1 + ∂ E d ∂ n e t 2 , 2 l ∂ n e t 2 , 2 l ∂ a 2 , 3 l − 1 = δ 1 , 2 l w 2 , 2 + δ 2 , 2 l w 1 , 2 \begin{aligned} \frac{\partial E_d}{\partial a_{2,3}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial n e t_{1,2}^l}{\partial a_{2,3}^{l-1}}+\frac{\partial E_d}{\partial n e t_{2,2}^l} \frac{\partial n e t_{2,2}^l}{\partial a_{2,3}^{l-1}} =\delta_{1,2}^l w_{2,2}+\delta_{2,2}^l w_{1,2}\end{aligned} ∂a2,3l−1∂Ed=∂net1,2l∂Ed∂a2,3l−1∂net1,2l+∂net2,2l∂Ed∂a2,3l−1∂net2,2l=δ1,2lw2,2+δ2,2lw1,2
∂ E d ∂ a 3 , 1 l − 1 = ∂ E d ∂ n e t 2 , 1 l ∂ n e t 2 , 1 l ∂ a 3 , 1 l − 1 = δ 2 , 1 l w 2 , 1 \begin{aligned} \frac{\partial E_d}{\partial a_{3,1}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{2,1}^l} \frac{\partial n e t_{2,1}^l}{\partial a_{3,1}^{l-1}} =\delta_{2,1}^l w_{2,1}\end{aligned} ∂a3,1l−1∂Ed=∂net2,1l∂Ed∂a3,1l−1∂net2,1l=δ2,1lw2,1
∂ E d ∂ a 3 , 2 l − 1 = ∂ E d ∂ n e t 2 , 1 l ∂ n e t 2 , 1 l ∂ a 3 , 2 l − 1 + ∂ E d ∂ n e t 2 , 2 l ∂ n e t 2 , 2 l ∂ a 3 , 2 l − 1 = δ 2 , 1 l w 2 , 2 + δ 2 , 2 l w 2 , 1 \begin{aligned} \frac{\partial E_d}{\partial a_{3,2}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{2,1}^l} \frac{\partial n e t_{2,1}^l}{\partial a_{3,2}^{l-1}}+\frac{\partial E_d}{\partial n e t_{2,2}^l} \frac{\partial n e t_{2,2}^l}{\partial a_{3,2}^{l-1}} =\delta_{2,1}^l w_{2,2}+\delta_{2,2}^l w_{2,1}\end{aligned} ∂a3,2l−1∂Ed=∂net2,1l∂Ed∂a3,2l−1∂net2,1l+∂net2,2l∂Ed∂a3,2l−1∂net2,2l=δ2,1lw2,2+δ2,2lw2,1
∂ E d ∂ a 3 , 3 l − 1 = ∂ E d ∂ n e t 2 , 2 l ∂ n e t 2 , 2 l ∂ a 3 , 3 l − 1 = δ 2 , 2 l w 2 , 2 \begin{aligned} \frac{\partial E_d}{\partial a_{3,3}^{l-1}} & =\frac{\partial E_d}{\partial n e t_{2,2}^l} \frac{\partial n e t_{2,2}^l}{\partial a_{3,3}^{l-1}} =\delta_{2,2}^l w_{2,2}\end{aligned} ∂a3,3l−1∂Ed=∂net2,2l∂Ed∂a3,3l−1∂net2,2l=δ2,2lw2,2
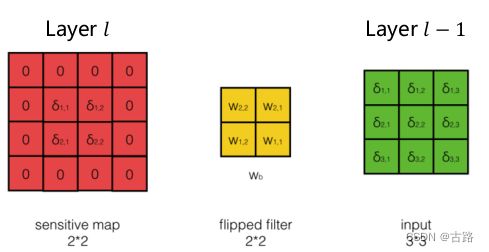
总结一下就是: ∂ E d ∂ a l − 1 = δ l ∗ W l \frac{\partial E_d}{\partial a^{l-1}}=\delta^l * W^l ∂al−1∂Ed=δl∗Wl
δ i , j l − 1 = ∂ E d ∂ n e t i , j I − 1 = ∂ E d ∂ a i , j l − 1 ∂ a i , j l − 1 ∂ n e t i , j l − 1 = ∑ m ∑ n w m , n l δ i + m , j + n l f ′ ( n e t i , j l − 1 ) δ l − 1 = δ l ∗ W l ∘ f ′ ( n e t l − 1 ) \begin{aligned} \delta_{i, j}^{l-1} & =\frac{\partial E_d}{\partial n e t_{i, j}^{I-1}} \\ & =\frac{\partial E_d}{\partial a_{i, j}^{l-1}} \frac{\partial a_{i, j}^{l-1}}{\partial n e t_{i, j}^{l-1}} \\ & =\sum_m \sum_n w_{m, n}^l \delta_{i+m, j+n}^l f^{\prime}\left(n e t_{i, j}^{l-1}\right) \\ \delta^{l-1}= & \delta^l * W^l \circ f^{\prime}\left(n e t^{l-1}\right) \end{aligned} δi,jl−1δl−1==∂neti,jI−1∂Ed=∂ai,jl−1∂Ed∂neti,jl−1∂ai,jl−1=m∑n∑wm,nlδi+m,j+nlf′(neti,jl−1)δl∗Wl∘f′(netl−1)
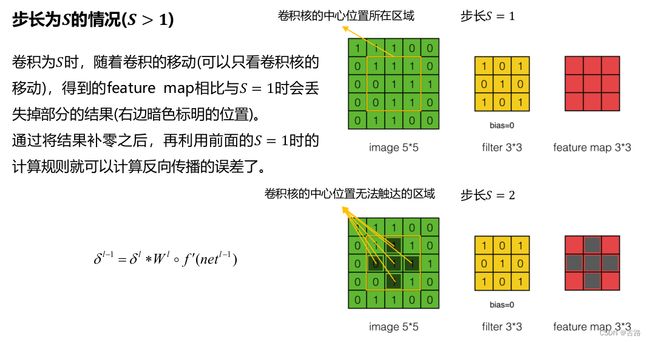
2.2.2.步长为S的情况
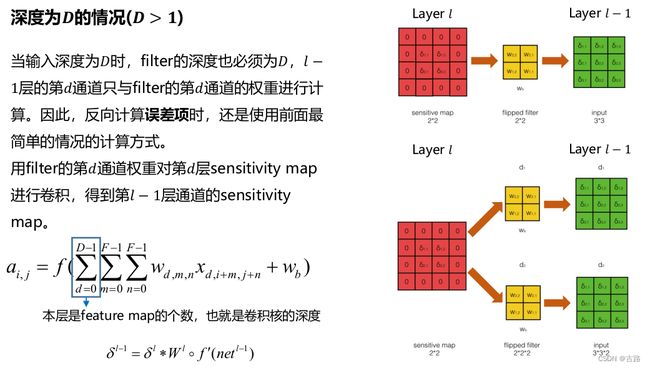
2.2.3.深度为D时候
例如图像 RGB 三个channel,D=3.
2.2.4.filter的数量为N的时候
2.2.5.N个filter,Depth为D
2.3.卷积层权重更新
在得到第l层sensitivity map的情况下,计算filter的权重的梯度,由于卷积层是权重共享的,因此梯度的计算稍有不同。
n e t 1 , 1 l = w 1 , 1 a 1 , 1 l − 1 + w 1 , 2 a 1 , 2 l − 1 + w 2 , 1 a 2 , 1 l − 1 + w 2 , 2 a 2 , 2 l − 1 + w b (1) n e t_{1,1}^l=w_{1,1} a_{1,1}^{l-1}+w_{1,2} a_{1,2}^{l-1}+w_{2,1} a_{2,1}^{l-1}+w_{2,2} a_{2,2}^{l-1}+w_b \tag{1} net1,1l=w1,1a1,1l−1+w1,2a1,2l−1+w2,1a2,1l−1+w2,2a2,2l−1+wb(1) n e t 1 , 2 l = w 1 , 1 a 1 , 2 l − 1 + w 1 , 2 a 1 , 3 l − 1 + w 2 , 1 a 2 , 2 l − 1 + w 2 , 2 a 2 , 3 l − 1 + w b (2) n e t_{1,2}^l=w_{1,1} a_{1,2}^{l-1}+w_{1,2} a_{1,3}^{l-1}+w_{2,1} a_{2,2}^{l-1}+w_{2,2} a_{2,3}^{l-1}+w_b \tag{2} net1,2l=w1,1a1,2l−1+w1,2a1,3l−1+w2,1a2,2l−1+w2,2a2,3l−1+wb(2) n e t 2 , 1 l = w 1 , 1 a 2 , 1 l − 1 + w 1 , 2 a 2 , 2 l − 1 + w 2 , 1 a 3 , 1 l − 1 + w 2 , 2 a 3 , 2 l − 1 + w b (3) n e t_{2,1}^l=w_{1,1} a_{2,1}^{l-1}+w_{1,2} a_{2,2}^{l-1}+w_{2,1} a_{3,1}^{l-1}+w_{2,2} a_{3,2}^{l-1}+w_b \tag{3} net2,1l=w1,1a2,1l−1+w1,2a2,2l−1+w2,1a3,1l−1+w2,2a3,2l−1+wb(3) n e t 2 , 2 l = w 1 , 1 a 2 , 2 l − 1 + w 1 , 2 a 2 , 3 l − 1 + w 2 , 1 a 3 , 2 l − 1 + w 2 , 2 a 3 , 3 l − 1 + w b (4) n e t_{2,2}^l=w_{1,1} a_{2,2}^{l-1}+w_{1,2} a_{2,3}^{l-1}+w_{2,1} a_{3,2}^{l-1}+w_{2,2} a_{3,3}^{l-1}+w_b \tag{4} net2,2l=w1,1a2,2l−1+w1,2a2,3l−1+w2,1a3,2l−1+w2,2a3,3l−1+wb(4)
∂ E d ∂ w 1 , 1 = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ w 1 , 1 + ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ w 1 , 1 + ∂ E d ∂ n t 2 , 1 l ∂ n e t 2 , 1 l ∂ w 1 , 1 + ∂ E d ∂ net 2 , 2 I ∂ n e t 2 , 2 l ∂ w 1 , 1 = δ 1 , 1 l a 1 , 1 l − 1 + δ 1 , 2 l a 1 , 2 l − 1 + δ 2 , 1 l a 2 , 1 l − 1 + δ 2 , 2 l a 2 , 2 l − 1 \begin{aligned} & \frac{\partial E_d}{\partial w_{1,1}}=\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial w_{1,1}}+\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial n e t_{1,2}^l}{\partial w_{1,1}}+\frac{\partial E_d}{\partial n t_{2,1}^l} \frac{\partial n e t_{2,1}^l}{\partial w_{1,1}}+\frac{\partial E_d}{\partial \text { net }_{2,2}^I} \frac{\partial n e t_{2,2}^l}{\partial w_{1,1}} \\ & =\delta_{1,1}^l a_{1,1}^{l-1}+\delta_{1,2}^l a_{1,2}^{l-1}+\delta_{2,1}^l a_{2,1}^{l-1}+\delta_{2,2}^l a_{2,2}^{l-1} \\ & \end{aligned} ∂w1,1∂Ed=∂net1,1l∂Ed∂w1,1∂net1,1l+∂net1,2l∂Ed∂w1,1∂net1,2l+∂nt2,1l∂Ed∂w1,1∂net2,1l+∂ net 2,2I∂Ed∂w1,1∂net2,2l=δ1,1la1,1l−1+δ1,2la1,2l−1+δ2,1la2,1l−1+δ2,2la2,2l−1 ∂ E d ∂ w 1 , 2 = δ 1 , 1 l a 1 , 2 l − 1 + δ 1 , 2 l a 1 , 3 l − 1 + δ 2 , 1 l a 2 , 2 l − 1 + δ 2 , 2 l a 2 , 3 l − 1 \frac{\partial E_d}{\partial w_{1,2}}=\delta_{1,1}^l a_{1,2}^{l-1}+\delta_{1,2}^l a_{1,3}^{l-1}+\delta_{2,1}^l a_{2,2}^{l-1}+\delta_{2,2}^l a_{2,3}^{l-1} ∂w1,2∂Ed=δ1,1la1,2l−1+δ1,2la1,3l−1+δ2,1la2,2l−1+δ2,2la2,3l−1 ∂ E d ∂ w 2 , 1 = δ 1 , 1 l a 2 , 1 l − 1 + δ 1 , 2 l a 2 , 2 l − 1 + δ 2 , 1 l a 3 , 1 l − 1 + δ 2 , 2 l a 3 , 2 l − 1 \frac{\partial E_d}{\partial w_{2,1}}=\delta_{1,1}^l a_{2,1}^{l-1}+\delta_{1,2}^l a_{2,2}^{l-1}+\delta_{2,1}^l a_{3,1}^{l-1}+\delta_{2,2}^l a_{3,2}^{l-1} ∂w2,1∂Ed=δ1,1la2,1l−1+δ1,2la2,2l−1+δ2,1la3,1l−1+δ2,2la3,2l−1 ∂ E d ∂ w 2 , 2 = δ 1 , 1 l a 2 , 2 l − 1 + δ 1 , 2 l a 2 , 3 l − 1 + δ 2 , 1 l a 3 , 2 l − 1 + δ 2 , 2 l a 3 , 3 l − 1 \frac{\partial E_d}{\partial w_{2,2}}=\delta_{1,1}^l a_{2,2}^{l-1}+\delta_{1,2}^l a_{2,3}^{l-1}+\delta_{2,1}^l a_{3,2}^{l-1}+\delta_{2,2}^l a_{3,3}^{l-1} ∂w2,2∂Ed=δ1,1la2,2l−1+δ1,2la2,3l−1+δ2,1la3,2l−1+δ2,2la3,3l−1 ∂ E d ∂ w b = ∂ E d ∂ n e t 1 , 1 l ∂ n e t 1 , 1 l ∂ w b + ∂ E d ∂ n e t 1 , 2 l ∂ n e t 1 , 2 l ∂ w b + ∂ E d ∂ net 2 , 1 l ∂ n e t 2 , 1 l ∂ w b + ∂ E d ∂ n e t 2 , 2 l ∂ n t 2 , 2 ′ ∂ w b = δ 1 , 1 l + δ 1 , 2 l + δ 2 , 1 l + δ 2 , 2 I = ∑ i ∑ j δ i , j l \begin{aligned} \frac{\partial E_d}{\partial w_b} & =\frac{\partial E_d}{\partial n e t_{1,1}^l} \frac{\partial n e t_{1,1}^l}{\partial w_b}+\frac{\partial E_d}{\partial n e t_{1,2}^l} \frac{\partial n e t_{1,2}^l}{\partial w_b}+\frac{\partial E_d}{\partial \text { net }_{2,1}^l} \frac{\partial n e t_{2,1}^l}{\partial w_b}+\frac{\partial E_d}{\partial n e t_{2,2}^l} \frac{\partial n t_{2,2}^{\prime}}{\partial w_b} \\ & =\delta_{1,1}^l+\delta_{1,2}^l+\delta_{2,1}^l+\delta_{2,2}^I \\ & =\sum_i \sum_j \delta_{i, j}^l \end{aligned} ∂wb∂Ed=∂net1,1l∂Ed∂wb∂net1,1l+∂net1,2l∂Ed∂wb∂net1,2l+∂ net 2,1l∂Ed∂wb∂net2,1l+∂net2,2l∂Ed∂wb∂nt2,2′=δ1,1l+δ1,2l+δ2,1l+δ2,2I=i∑j∑δi,jl