比较横截面与时间序列的因子模型
发表于2020年Review of Financial Studies上的"Comparing cross-section and time-series factor models"一文,作者是2013年诺贝尔经济学奖得主、芝加哥大学Booth商学院的Eugene F. Fama,和他的老搭档、达特茅斯学院Amos Tuck商学院的Kenneth R. French,这也是二位的最新一次合作。
该文十分简单,且为纯实证,本文对其关键部分作个剖析。
在下文中,用CS(Cross-Section)表示“横截面”一词,用TS(Time-Series)表示“时间序列”一词。
1 实证模型
在因子模型中,资产的收益率应由资产在因子上的载荷,乘上因子收益率构成。有了因子收益率,就可以回归得到因子载荷,而有了载荷,也可以回归得到因子收益率,到底应该用哪种方式呢?该文共比较了4种模型。
第一个模型,使用Fama和MacBeth(1973)的CS回归方法,直接用公司特征作为载荷,用CS回归,得到的系数就是因子收益率:
R i t = R z t + R M C t M C i t − 1 + R B M t B M i t − 1 + R O P t O P i t − 1 + R I N V t I N V i t − 1 + e i t (1) \begin{aligned} R_{it}=&R_{zt}+R_{MCt}MC_{it-1}+R_{BMt}BM_{it-1}\\ &+R_{OPt}OP_{it-1}+R_{INVt}INV_{it-1}+e_{it} \tag{1} \end{aligned} Rit=Rzt+RMCtMCit−1+RBMtBMit−1+ROPtOPit−1+RINVtINVit−1+eit(1)
这样得出的因子,称为CS因子。
然后,将截距项移到左边,将自变量与系数交换位置,就成了一个资产定价模型:
R i t − R z t = M C i t − 1 R M C t + B M i t − 1 R B M t + O P i t − 1 R O P t + I N V i t − 1 R I N V t + e i t (2) \begin{aligned} R_{it}-R_{zt}=&MC_{it-1}R_{MCt}+BM_{it-1}R_{BMt}\\ &+OP_{it-1}R_{OPt}+INV_{it-1}R_{INVt}+e_{it} \tag{2} \end{aligned} Rit−Rzt=MCit−1RMCt+BMit−1RBMt+OPit−1ROPt+INVit−1RINVt+eit(2)
第二个模型,就是先通过Fama和French(2015)中构造的TS因子的方法,即用多空组合的方式,构造出因子的收益率序列,然后,再以TS因子收益率为自变量,进行TS回归,得到的系数就是载荷:
R i t − R f t = a i + b i ( R m t − R f t ) + s i S M B t + h i H M L t + r i R M W t + c i C M A t + e i t (3) \begin{aligned} R_{it}-R_{ft}=&a_i+b_i(R_{mt}-R_{ft})+s_i {SMB}_t+ h_i HML_t \\ &+r_i RMW_t + c_i CMA_t+e_{it} \tag{3} \end{aligned} Rit−Rft=ai+bi(Rmt−Rft)+siSMBt+hiHMLt+riRMWt+ciCMAt+eit(3)
第三个模型,用(1)中得出的CS因子,替换(3)中的TS因子,同样进行TS回归,得到载荷:
R t − R f t = a i + b 1 i ( R m t − R f t ) + b 2 i R M C t + b 3 i R B M t + b 4 i R O P t + b 5 i R I N V t + e i t (4) \begin{aligned} R_t-R_{ft}=&a_i+b_{1i}(R_{mt}-R_{ft})+b_{2i} R_{MCt}+ b_{3i} R_{BMt}\\ &+b_{4i} R_{OPt} + b_{5i} R_{INVt} +e_{it} \tag{4} \end{aligned} Rt−Rft=ai+b1i(Rmt−Rft)+b2iRMCt+b3iRBMt+b4iROPt+b5iRINVt+eit(4)
(3)与(4)得到的载荷都不是时变的,为了引入时变载荷,可以在系数中加入时变的CS因子,即加入交叉项:
R i t − R f t = a i + b i ( R m t − R f t ) + s i S M B t + h i H M L t + r i R M W t + c i C M A t + s i 2 M C i t − 1 S M B t + h i 2 B M i t − 1 H M L t + r i 2 O P i t − 1 R M W t + c i 2 I N V i t − 1 C M A t + e i t (5) \begin{aligned} R_{it}-R_{ft}=&a_i+b_i(R_{mt}-R_{ft})+s_i {SMB}_t+ h_i HML_t \\ &+r_i RMW_t + c_i CMA_t\\ &+s_{i2}MC_{it-1}{SMB}_t+h_{i2}BM_{it-1}HML_t\\ &+r_{i2}OP_{it-1} RMW_t + c_{i2} INV_{it-1} CMA_t+e_{it} \tag{5} \end{aligned} Rit−Rft=ai+bi(Rmt−Rft)+siSMBt+hiHMLt+riRMWt+ciCMAt+si2MCit−1SMBt+hi2BMit−1HMLt+ri2OPit−1RMWt+ci2INVit−1CMAt+eit(5)
(2)(3)(4)(5)组成了要检验的4个模型。
2 数据
2.1 因子构建
对于FF(2015)的五因子模型即方程(3),在每个6月底生成一次规模SMB、价值HML、盈利RMW、投资CMA的TS因子。
HML(High Minus Low)因子:用NYSE的6月底的中位数MC(市值)作为断点,将NYSE、AMEX、NASDQA的所有股票分入高/低市值组;再独立地用NYSE股票的BM的 3 0 t h 30^{th} 30th和 7 0 t h 70^{th} 70th分位数作为断点,分成3组。 T T T年6月的BM,就是 T − 1 T-1 T−1年财年末的账面净值与 T − 1 T-1 T−1年12月底市值(在12月到财年末,若在外发行股票数可能有变化,则需要调整)的比率,再取对数。这样就可以得到 2 × 3 2\times 3 2×3个市值加权(VW,value-weight)组合。HML是大市值分组中的高低BM组合收益率之差,与小市值分组中的高低BM组合收益率之差,取平均数。
RMW(Robust Minus Weak)、CMA(Conservative Minus Aggressive)因子:做法与HML类似,生成RMW时用OP(Operating profitbality),生成CMA时用INV(Investment)。
SMB(Small Minus Big)因子:前面一共得到3个 2 × 3 2\times 3 2×3组合,用其中的9个小市值组合的平均收益率减去剩下的9个大市值组合的平均收益率,即为SMB因子。
UMD(Up Minus Down)因子:先用从 t − 12 t-12 t−12月到 t − 2 t-2 t−2月的累计收益率除以11,作为MOM,再用MOM作为第二个因子构造 2 × 3 2\times 3 2×3组合,得到UMD因子,它是月度更新的。
MC、BM、OP、INV、MOM等公司特征:就是构造以上因子所用到的公司特征。个股的BM、OP、INV在每年6月更新,MC和MOM在每个月更新。组合的特征就是组合中股票的VW平均值,权重(市值)每个月更新。
构造CS因子,每个月进行(1)式回归,对每个RHS的公司特征做z-score处理,在不加入MOM时用18个组合做标准化,在加入MOM时用24个组合做标准化。在做标准化之后,CS水平收益率 R z t R_{zt} Rzt就是18或24个LHS资产收益率的等权重均值。
构建因子的LHS资产:为使CS和TS因子可比,月度回归(1)式的左侧资产选择18个生成了SMB、HML、RMW、CMA的VW组合。如果模型中要用到CS动量因子,也加入生成UMD的6个VW组合。
2.2 描述性统计
表1为上述因子的描述性统计,Panel A为TS因子,Panel B为CS因子。样本区间为1963.7–2018.8,共662个月度收益率。
我们知道OLS回归得到的系数为 β ^ = ( X ′ X ) − 1 X ′ y \hat{\beta} = (X'X)^{-1}X'y β^=(X′X)−1X′y,也就是 y y y的线性组合。那么(1)式中系数就是 R z t R_{zt} Rzt和CS因子的收益率,也就是说,它们其实是由LHS资产的收益率线性组合出来的。那么,组成它们的,不同的LHS资产的权重是多少呢?表2列出了结果。
2.3 用于测试的LHS资产
在实证中,用于检验的LHS资产使用每年6月更新的MC和BM、OP、INV的 3 3 3组 5 × 5 5\times 5 5×5组合,再加上月度更新的MC和MOM的 5 × 5 5\times 5 5×5组合。注意,用于生成因子的LHS资产还是以前的 2 × 3 2\times 3 2×3组合,但用于检验的是 5 × 5 5\times 5 5×5组合。
为增加一些挑战性,再在LHS中加入FF(2016)的异象组合:
- 长期困扰CAPM的单变量市场beta与平均收益率的扁平关系(flat relation);
- 股票回购后的高平均收益率,与股票发行后的低平均收益率;
- 应计利润大的公司,平均收益率较低;
- 日收益率方差大的公司,平均收益率较低。
同样使用MC和这些异象变量的NYSE的5分位数,构造 5 × 5 5\times 5 5×5组合。但这里有几个例外:一是股票净发行(NI,Net share Issue)需要用7分位数,即净回购、无回购无发行,以及净发行的5分位数;二是大市值股票中几乎没有高收益率波动的,因此不适合使用独立双重排序,只能在MC排序后的基础上再进行排序。
MC-VAR组合是月度更新的,而其他异象组合都在每年6月底更新。
3 模型比较标准
该文用了多种模型比较标准。在这里用 A A A和 V V V表示横截面的均值方差, a a a表示模型产生的截距向量,比较标准有:
- A ∣ a ∣ A|a| A∣a∣:截距项绝对值的均值;
- A ∣ t ( a ) ∣ A|t(a)| A∣t(a)∣:截距项的 t t t值的绝对值的均值;
- A a 2 V r ˉ \dfrac{A a^2}{V \bar r} VrˉAa2:和下面一个一样,都是度量截面的分散程度,分子为截距平方的均值, V r ˉ {V \bar r} Vrˉ为LHS资产的平均收益率的截面方差;
- A λ 2 V r ˉ \dfrac{A \lambda^2}{V \bar r} VrˉAλ2:修正截距的平方为 λ 2 ≡ a 2 − s 2 ( a ) \lambda^2 \equiv a^2-s^2(a) λ2≡a2−s2(a),这是因为在估计截距时有噪声;
- A R 2 AR^2 AR2:回归 R 2 R^2 R2的均值;
- A s ( a ) As(a) As(a):截距标准误的均值;
- A s ( e ) As(e) As(e):残差标准差的均值;
- S h 2 ( a ) Sh^2(a) Sh2(a):截距的最大平方夏普比率,用 Σ \Sigma Σ表示回归残差的协方差矩阵,则 S h 2 ( a ) = a ′ Σ a Sh^2(a)=a'\Sigma a Sh2(a)=a′Σa;
- G R S GRS GRS:GRS统计量;
- p ( G R S ) p(GRS) p(GRS):GRS统计量的p值;
- T 2 T^2 T2:Hotelling’s T 2 T^2 T2;
- p ( T 2 ) p(T^2) p(T2):Hotelling’s T 2 T^2 T2的 p p p值。
4 实证结果
4.1 总体结果
实证结果在表3中,其中Panel A1和Panel A2检验了模型(3)、(4),Panel A3、Panel A4检验了模型(5)。
在检验模型(3)、(4)、(5)时,都是用TS回归,然后将各资产回归得到的截距项放在一起,形成向量 a a a。但由于模型(2)是从CS回归中变化而来,可以不再做TS回归。Panel B1和Panel B2是使用CS因子对测试LHS资产相对 R z t R_{zt} Rzt的超额收益率做回归的情况,而Panel B3–B6则不再做TS回归。
在Panel B5和Panel B6中,模型(2)中的 R z R_z Rz和CS因子是用(1)式由不同 2 × 3 2\times 3 2×3组合生成的,接着,用每个LHS测试资产的公司特征做加权平均,用生成CS因子时的18个或24个组合的均值和标准差对它做标准化,最后的值作为LHS测试资产的因子载荷,再乘上事先得到的CS因子的收益率,去预测LHS测试资产的相对 R z t R_{zt} Rzt的超额收益率,从而得到每个LHS资产在每个月的预测误差。在Panel B3和Panel B4中,用特征的时间序列均值作为CS因子的载荷。在这4个Panel中,载荷不是被估计出来的,因此GRS检验不适用,只能用Hotelling’s T 2 T^2 T2检验。
在每一个评价标准上,Panel B5、B6的结果都比Panel A好。
4.2 去除异象组合后的结果
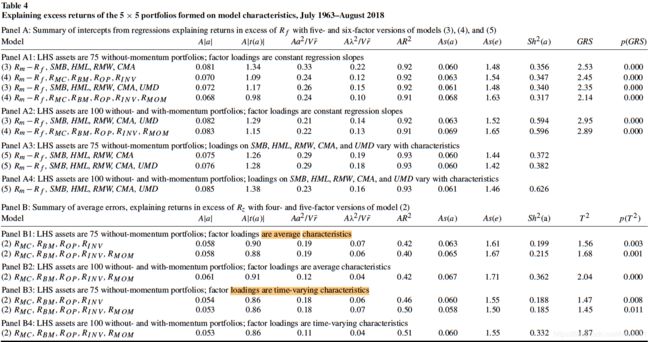
表4就是在表3的LHS测试资产中剔除了异象组合后的结果,它使用的LHS资产是4组 5 × 5 5\times 5 5×5组合,即MC-BM、MC-OP、MC-INV、MC-MOM组合。
在原文的附录中,表A1-A4报告了每个 5 × 5 5\times 5 5×5组合的结果。
4.3 在异象组合中的结果
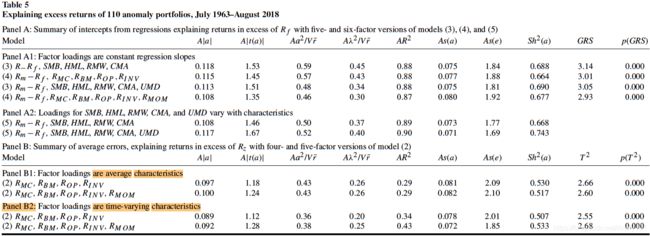
表5是只在110个异象组合中的结果。
在原文的附录中,表A5-A8报告了每种异象组合的结果。
可以看到,不管用什么作为LHS测试资产,模型(2)结果都是最好的,结论稳健。
参考文献
- Fama, E. F., and K. R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics.
- Fama, E. F., and K. R. French. 2020. Comparing Cross-Section and Time-Series Factor Models. Review of Financial Studies.
- Fama, E. F., and J. D. MacBeth. 1973. Risk, return, and equilibrium: empirical tests. Journal of Political Economy.