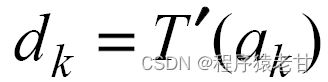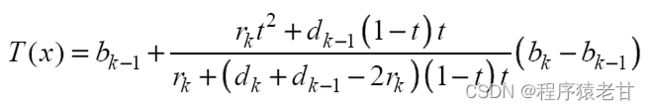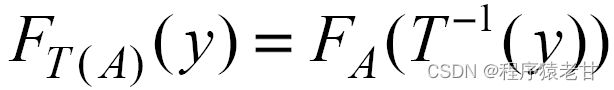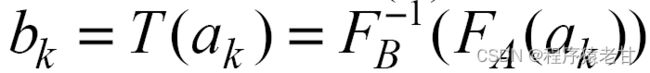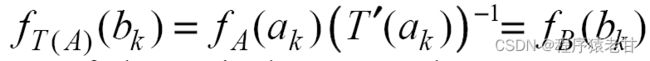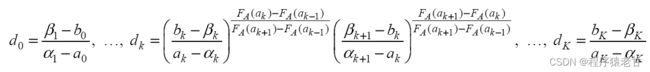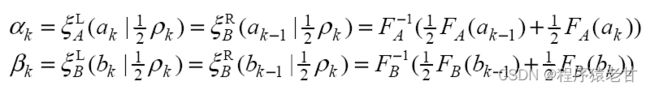基于颜色直方图优化的图像增强方法
最近改图像颜色迁移的论文,审稿人要求补充基于直方图优化的方法细节。趁此机会,我重新下载了相关文献,决定重新学习下该类方法,并把一些细节记录在本篇博客中,供交流学习。
目录
1. 前言
2. 背景知识
3. 颜色变换
4. 颜色匹配
5. 颜色对比度
6. 实验结果
总结
Reference
1. 前言
在之前的博客中,我们已经系统的介绍了颜色迁移的一些比较主流的工作:
图像颜色迁移专题介绍(一): Global Color Transfer_程序猿老甘的博客-CSDN博客_颜色迁移图像颜色迁移专题介绍(二): Correspondence_程序猿老甘的博客-CSDN博客_遥感图像颜色迁移
图像颜色迁移专题介绍(三): Deep Examplar-based Colorization_程序猿老甘的博客-CSDN博客_基于深度学习的色彩迁移
基于GMM模型的图像分割与颜色迁移算法_程序猿老甘的博客-CSDN博客_gmm 图像分割
这些工作从全局颜色对应,语义分析,低维图像特征相似度等角度,尝试提升颜色迁移的精确度。基于颜色直方图优化的方法同样可以被看做是颜色迁移或颜色加强的一种解决方案。其优势在于,直方图优化脱离了图像的语义,从颜色分布的全局角度来估算源图像和目标图像的对应关系。同时,由于考虑到直方图本身颜色分布的一些统计特性,使得颜色映射能够考虑部分局部的颜色匹配关系,而该过程又独立于图像的位置于语义信息。这些特点使得颜色直方图优化方法具备一些与众不同的性能优势。本文基于论文[1]的相关内容,来展开介绍下基于直方图优化的图像增强方法。
2. 背景知识
直方图优化的基础实现是基于累积分布函数以产生一个均匀分布。具体的实现方法包括:树搜索[2],整数线性规划[3],动态规划[4],或者直方图度量[5]。严格来说,利用上述方法可以派生一个中间映射,以平衡各方面的映射需求,完成复杂的直方图优化任务。这些方法能够生成一个离散的映射来减少量化差异,同时不考虑源图像直方图的失真。这为源图像到目标图像的直方图优化匹配创造了条件。
最简单的直方图优化方法是线性变换,一般用来指定图像颜色分布的范围,均值或者标准差。优化高阶的统计变量是比较困难的,这时候就需要非线性数值优化。一个更灵活的方法是将直方图视为一个嵌套区间树,以实现一个分级的线性变换。不过,分段线性映射缺少灵活性,其不能保证映射变换是连续可微的并保持单调性。文献[1]提供了一个方案,以解决当前分段映射方法的问题。
另外,针对颜色的图像增强方法,需要选定对应的颜色空间,以实现对颜色分布的调整。传统的颜色空间最大的问题在于各个信息通道具有耦合性,不利于独立优化。根据Reinhard的相关工作,使用CIE Lab color space对颜色的解耦表达具有天然的优势。因此,利用该颜色空间实现对直方图优化算法,能够降低优化任务的耦合性,以得到更好的结果。
3. 颜色变换
类似于传统的分段线性映射,文献[1]的方法主要还是以来建立几个关键颜色的对应关系,使用位移来决定颜色偏移,坡度决定对比度。
a_k为源图像的关键颜色,b_k为参考图像的关键颜色。映射T决定了两幅图像关键颜色的对应关系。自然,T应该满足一阶的连续关系,即对比度调整。这里,使用一个分段定义,并使用插值样条来确保这些参数的局部有效性。唯一的约束是,参数必须满足一个单调函数,即:
除了保证不可逆性,单调函数还需要保持颜色的自然顺序,从而避免由图像对比度的局部反转引起的颜色分布异常。变换需要保持连续性(包括一阶连续),以防止畸变,进而产生错误的边缘。为了满足这些要求,我们的直方图优化依赖于分段有理插值样条[6]:
对于直方图的拉伸与压缩过度,都会导致颜色分布的异常。对于一个区域的对比度增强,必然意味着其他区域的对比度压缩。这种权衡取决于变换函数的选择。相对来说,分段有理插值样条与适度的形状参数控制能够得到较好的结果。
4. 颜色匹配
直方图优化的最终目的是按照参考图像的颜色分布,改变源图像的颜色分布。这里我们假设概率密度函数f,累计分布F,及其分位数F^-1。 所得变换函数y=T(x)的预期目标为:
约束用于使得源图像的颜色分布趋近于参考图像。精确的直方图优化,使用:
分段的重建目标分布,使得对比度的影响
为拉伸更可能的区域并压缩较不可能拉伸的区域。通常,目标是保留配色方案,而不是必须重现颜色直方图。由于色彩平衡体现在整体形状的分布上,而直方图之间的微小差异往往可以低于视觉感知的阈值。因此精确的直方图优化是不必要的。我们只关注统计意义上的直方图匹配。
一个恰当的变换需要在颜色和对比度上,保持循序渐进和有控制变换过程。因此,文献[1]所提的算法专注于一些具有代表性的关键颜色的对应关系上,用以表达颜色分布相关的特征信息:
该方法映射一组源图像的关键颜色q_k![]() ,到关联的参考图像分布的累积分布函数的分位数
,到关联的参考图像分布的累积分布函数的分位数![]() 。因此,源图像的范围
。因此,源图像的范围![]() 就可以匹配目标图像的范围
就可以匹配目标图像的范围![]() 。关键颜色的数量决定了变换的精度。
。关键颜色的数量决定了变换的精度。
5. 颜色对比度
关键颜色的对比度调整控制其对应的局部变换。对比度调整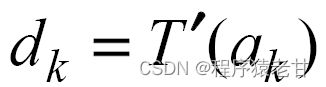 服务于直方图优化的精度调整以及畸变控制。这里对d_k的范围首先要加以控制:
服务于直方图优化的精度调整以及畸变控制。这里对d_k的范围首先要加以控制:![]()
![]() ;注意保持关键颜色的对比度,设置d_k = 1。只对关键颜色之间的中间颜色进行调整。在关键颜色执行精确的直方图优化,通过设置对比度调整
;注意保持关键颜色的对比度,设置d_k = 1。只对关键颜色之间的中间颜色进行调整。在关键颜色执行精确的直方图优化,通过设置对比度调整![]() 实现。这样:
实现。这样:
我们避免直接使用源直方图和目标直方图之间的比率。因为来自图像数据的原始直方图在变换中,表现出大量的小范围变化,使得对比度变化从关键颜色扩展到中间颜色。这里作者给出使用最近邻估算 [7] 来平滑这种小范围变化。这里原作者给出了一个由梯度与最近邻推导出来的对比度调节公式,涉及概率密度计算。我将公式列在此处(具体的解释参看原文):
6. 实验结果
交叉颜色迁移结果:
总结
本文系统的介绍了直方图优化方面的一些基本问题,包括关键颜色对应,中间颜色调整,对比度优化等。同时,该文解释了如何利用颜色空间,直方图匹配,样条插值,概率密度函数等工具解决颜色编辑或颜色迁移的实际问题。总体来说,对于想要切入直方图优化方法的同学,本文还是由不少干货的。我的解读只是做点表面功夫,要想深入了解具体的实现细节,还是要花些时间认真学习。
Reference
[1] M. Grundland, Dodgson NA. Color histogram specification by histogram warping [C]. COLOR IMAGING X: PROCESSING, HARDCOPY, AND APPLICATIONS. 2005.
[2] SK. Chang, YW. Wong. Optimal histogram matching by monotone gray level transformation[J]. Communications of the Acm, 1978, 21(10):835-840.
[3] M. Mee, PP. Vaidyanathan. Optimal histogram modification with MSE metric[C]// Acoustics, Speech, and Signal Processing, 2001. Proceedings. (ICASSP '01). 2001 IEEE International Conference on. IEEE, 2001.
[4] IJ. Cox, S. Roy, SL. Hingorani. Dynamic histogram warping of image pairs for constant image brightness [C]. International Conference on Image Processing. IEEE, 1995.
[5] J. Morovic, J. Shaw, PL. Sun. A fast, non-iterative and exact histogram matching algorithm [J]. Pattern Recognition Letters, 2002, 23(1/3):127-135.
[6] JA. Gregory, R. Delbourgo. Piecewise Rational Quadratic Interpolation to Monotonic Data[J]. IMA Journal of Numerical Analysis, 1982, 2(2).
[7] DW. Scott. Multivariate Density Estimation: Theory, Practice, and Visualization[M]. 2008.