深度学习-函数-tf.nn.embedding_lookup 与tf.keras.layers.Embedding
embedding函数用法
- 1. one_hot编码
-
- 1.1. 简单对比
- 1.2.优势分析:
- 1.3. 缺点分析:
- 1.4. 延伸思考
- 2. embedding的用途
-
- 2.1 embedding有两个用途:
-
- 1、降维,如下图:2*6矩阵乘上6*3矩阵,得到2*3矩阵,维数减少
- 2、升维,原理同上
- 3. embedding的原理
- 4. embedding的作用
- 5. embedding的生成
- 6. embedding的使用
-
- 6.1. tf.nn.embedding_lookup 函数在TF1.x
-
- 6.1.1 ids只有一行
- 6.1.2 如果ids是多行
- 6.1.3 例子
- 6.2. tf.keras.layers.Embedding 函数在TF2.x 中
- 6.2. tf.keras.layers.Embedding 函数传入权重在TF2.x 中
- 7. 参考资料
1. one_hot编码
首先,了解下什么是one_hot编码,直接举例子如下:
词库
我 从 哪 里 来 要 到 何 处 去
0 1 2 3 4 5 6 7 8 9
__one_hot编码__如下:
# 我从哪里来,要到何处去
[
[1 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0]
[0 0 0 0 0 0 1 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 0 0 1]
]
# 我从何处来,要到哪里去
[
[1 0 0 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0 0 0]
[0 0 0 0 0 0 1 0 0 0]
[0 0 1 0 0 0 0 0 0 0]
[0 0 0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 1]
]
one_hot编码后,一个句子可以用一个矩阵表示,出现在词库中的词对应在矩阵中位置为1
1.1. 简单对比
one_hot编码之前使用列表(一维)表达一个句子
one_hot编码之后使用矩阵(二维)表达一个句子
1.2.优势分析:
1、稀疏矩阵做矩阵计算的时候,只需要把1对应位置的数相乘求和就行,
2、one-hot编码的优势就体现出来了,计算方便快捷、表达能力强
1.3. 缺点分析:
1、过于稀疏时,过度占用资源
比如:中文大大小小简体繁体常用不常用有十几万,然后一篇文章100W字,要表达所有句子,需要100W X 10W的矩阵
1.4. 延伸思考
1、如果我们的文章有100W字,99W是重复的,有1W是不重复的,我们是不是可以用1W X 10W的矩阵存储空间?这就是embedding的用途
2. embedding的用途
2.1 embedding有两个用途:
1、降维,如下图:26矩阵乘上63矩阵,得到2*3矩阵,维数减少
2、升维,原理同上
3. embedding的原理
可以参考这篇文章介绍的特别清楚
one_hot编码矩阵如下:
公主很漂亮:
公 [0 0 0 0 1]
主 [0 0 0 1 0]
很 [0 0 1 0 0]
漂 [0 1 0 0 0]
亮 [1 0 0 0 0]
扩大词库后:
公 [0 0 0 0 1 0 0 0 0 0]
主 [0 0 0 1 0 0 0 0 0 0]
很 [0 0 1 0 0 0 0 0 0 0]
漂 [0 1 0 0 0 0 0 0 0 0]
亮 [1 0 0 0 0 0 0 0 0 0]
在这基础上,王妃很漂亮表示为:
王 [0 0 0 0 0 0 0 0 0 1]
妃 [0 0 0 0 0 0 0 0 1 0]
很 [0 0 1 0 0 0 0 0 0 0]
漂 [0 1 0 0 0 0 0 0 0 0]
亮 [1 0 0 0 0 0 0 0 0 0]
从中文表示来看,我们可以感觉到,王妃跟公主其实是有很大关系的,比如:公主是皇帝的女儿,王妃是皇帝的妃子,可以从“皇帝”这个词进行关联上;公主住在宫里,王妃住在宫里,可以从“宫里”这个词关联上;公主是女的,王妃也是女的,可以从“女”这个字关联上
公主王妃one_hot编码
公 [0 0 0 0 1 0 0 0 0 0]
主 [0 0 0 1 0 0 0 0 0 0]
王 [0 0 0 0 0 0 0 0 0 1]
妃 [0 0 0 0 0 0 0 0 1 0]
通过刚才的假设关联,我们关联出了“皇帝”、“宫里”和“女”三个词,那我们尝试这么去定义公主和王妃
公主一定是皇帝的女儿,我们假设她跟皇帝的关系相似度为1.0;公主从一出生就住在宫里,直到20岁才嫁到府上,活了80岁,我们假设她跟宫里的关系相似度为0.25;公主一定是女的,跟女的关系相似度为1.0;
王妃是皇帝的妃子,没有亲缘关系,但是有存在着某种关系,我们就假设她跟皇帝的关系相似度为0.6吧;妃子从20岁就住在宫里,活了80岁,我们假设她跟宫里的关系相似度为0.75;王妃一定是女的,跟女的关系相似度为1.0;
于是,
皇 宫
帝 里 女
公主 [ 1.0 0.25 1.0]
王妃 [ 0.6 0.75 1.0]
这样我们就把公主和王妃两个词,跟皇帝、宫里、女这几个字(特征)关联起来了,我们可以认为:
公主=1.0 皇帝 +0.25宫里 +1.0女
王妃=0.6 皇帝 +0.75宫里 +1.0女
或者如下表示,
皇 宫
帝 里 女
公 [ 0.5 0.125 0.5]
主 [ 0.5 0.125 0.5]
王 [ 0.3 0.375 0.5]
妃 [ 0.3 0.375 0.5]
我们把皇帝叫做特征(1),宫里叫做特征(2),女叫做特征(3),于是乎,我们就得出了公主和王妃的隐含特征关系:
王妃=公主的特征(1)* 0.6 +公主的特征(2)* 3 +公主的特征(3)* 1
于是,我们把文字的one-hot编码,从稀疏态变成了密集态,并且让相互独立向量变成了有内在联系的关系向量
4. embedding的作用
就是把稀疏矩阵变成一个密集矩阵,也称为查表,因为他们之间是一个一一映射关系。
这种关系在反向传播的过程中,是一直在更新的,因此能在多次epoch后,使得这个关系变成相对成熟。
5. embedding的生成
TF1.X 是函数 tf.nn.embedding_lookup
TF2.X 是函数 layers.Embedding(input_dim=**, output_dim=, input_length=),
6. embedding的使用
6.1. tf.nn.embedding_lookup 函数在TF1.x
关于np.random.RandomState、np.random.rand、np.random.random、np.random_sample参考https://blog.csdn.net/lanchunhui/article/details/50405670
tf.nn.embedding_lookup函数的用法主要是选取一个张量里面索引对应的元素。tf.nn.embedding_lookup(params, ids):params可以是张量也可以是数组等,id就是对应的索引,其他的参数不介绍。
例如:
6.1.1 ids只有一行
import tensorflow as tf
#c = np.random.random([10, 1]) # 随机生成一个10*1的数组
#b = tf.nn.embedding_lookup(c, [1, 3])#查找数组中的序号为1和3的
p=tf.Variable(tf.random_normal([10,1]))#生成10*1的张量
b = tf.nn.embedding_lookup(p, [1, 3])#查找张量中的序号为1和3的
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print(sess.run(b))
#print(c)
print(sess.run(p))
print(p)
print(type(p))
输出:
[[0.15791859]
[0.6468804 ]]
[[-0.2737084 ]
[ 0.15791859]
[-0.01315552]
[ 0.6468804 ]
[-1.4090979 ]
[ 2.1583703 ]
[ 1.4137447 ]
[ 0.20688428]
[-0.32815856]
[-1.0601649 ]]
<tf.Variable 'Variable:0' shape=(10, 1) dtype=float32_ref>
<class 'tensorflow.python.ops.variables.Variable'>
分析:输出为张量的第一和第三个元素。
6.1.2 如果ids是多行
import tensorflow as tf
import numpy as np
a = [[0.1, 0.2, 0.3], [1.1, 1.2, 1.3], [2.1, 2.2, 2.3], [3.1, 3.2, 3.3], [4.1, 4.2, 4.3]]
a = np.asarray(a)
idx1 = tf.Variable([0, 2, 3, 1], tf.int32)
idx2 = tf.Variable([[0, 2, 3, 1], [4, 0, 2, 2]], tf.int32)
out1 = tf.nn.embedding_lookup(a, idx1)
out2 = tf.nn.embedding_lookup(a, idx2)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
print sess.run(out1)
print out1
print '=================='
print sess.run(out2)
print out2
输出:
[[ 0.1 0.2 0.3]
[ 2.1 2.2 2.3]
[ 3.1 3.2 3.3]
[ 1.1 1.2 1.3]]
Tensor("embedding_lookup:0", shape=(4, 3), dtype=float64)
==================
[[[ 0.1 0.2 0.3]
[ 2.1 2.2 2.3]
[ 3.1 3.2 3.3]
[ 1.1 1.2 1.3]]
[[ 4.1 4.2 4.3]
[ 0.1 0.2 0.3]
[ 2.1 2.2 2.3]
[ 2.1 2.2 2.3]]]
Tensor("embedding_lookup_1:0", shape=(2, 4, 3), dtype=float64)
6.1.3 例子
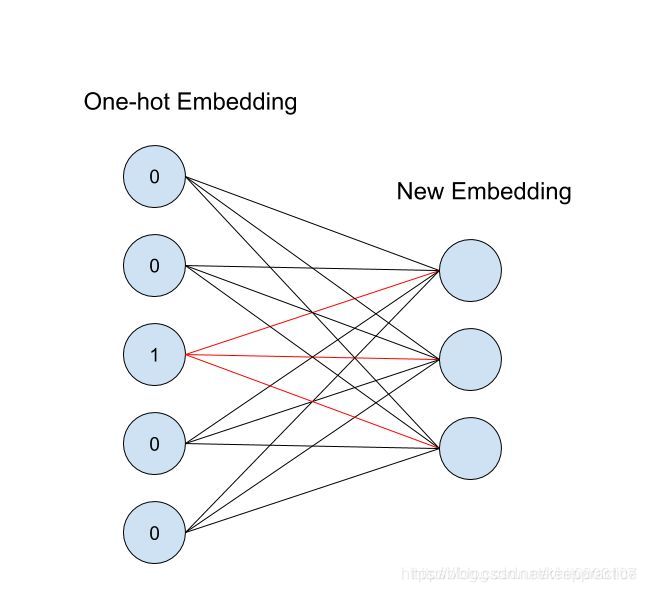
从id(索引)找到对应的One-hot encoding,然后红色的weight就直接对应了输出节点的值
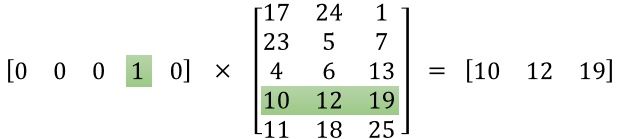
从one_hot到矩阵编码的转换过程需要在embedding进行查找:
one_hot * embedding_weights = embedding_code
import tensorflow as tf
import numpy as np
input_ids = tf.placeholder(dtype=tf.int32, shape=[None])
_input_ids = tf.placeholder(dtype=tf.int32, shape=[3, 2])
embedding_param = tf.Variable(np.identity(8, dtype=np.int32)) # 生成一个8x8的单位矩阵
input_embedding = tf.nn.embedding_lookup(embedding_param, input_ids)
_input_embedding = tf.nn.embedding_lookup(embedding_param, _input_ids)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
print('embedding:')
print(embedding_param.eval())
var1 = [1, 2, 6, 4, 2, 5, 7]
print('\n var1:')
print(var1)
print('\nprojecting result:')
print(sess.run(input_embedding, feed_dict={input_ids: var1}))
var2 = [[1, 4], [6, 3], [2, 5]]
print('\n _var2:')
print(var2)
print('\n _projecting result:')
print(sess.run(_input_embedding, feed_dict={_input_ids: var2}))
执行结果
embedding:
[[1 0 0 0 0 0 0 0]
[0 1 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0]
[0 0 0 1 0 0 0 0]
[0 0 0 0 1 0 0 0]
[0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 1 0]
[0 0 0 0 0 0 0 1]]
var1:
[1, 2, 6, 4, 2, 5, 7]
projecting result:
[[0 1 0 0 0 0 0 0]
[0 0 1 0 0 0 0 0]
[0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 0 0]
[0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0]
[0 0 0 0 0 0 0 1]]
_var2:
[[1, 4], [6, 3], [2, 5]]
_projecting result:
[[[0 1 0 0 0 0 0 0]
[0 0 0 0 1 0 0 0]]
[[0 0 0 0 0 0 1 0]
[0 0 0 1 0 0 0 0]]
[[0 0 1 0 0 0 0 0]
[0 0 0 0 0 1 0 0]]]
Process finished with exit code 0
6.2. tf.keras.layers.Embedding 函数在TF2.x 中
tf.keras.layers.Embedding
Arguments:
input_dim: int > 0. Size of the vocabulary,
i.e. maximum integer index + 1.
output_dim: int >= 0. Dimension of the dense embedding.
例子 -
import tensorflow as tf
import numpy as np
model = tf.keras.Sequential()
model.add(tf.keras.layers.Embedding(1000, 64, input_length=10))
# The model will take as input an integer matrix of size (batch,
# input_length), and the largest integer (i.e. word index) in the input
# should be no larger than 999 (vocabulary size).
# Now model.output_shape is (None, 10, 64), where `None` is the batch
# dimension.
input_array = np.random.randint(1000, size=(32, 10))
print(input_array)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print(output_array.shape)
执行结果
[[988 830 373 434 333 520 601 316 871 342]
[241 351 83 855 512 374 687 192 910 995]
[820 368 967 744 445 15 894 331 832 143]
[648 120 239 108 575 853 644 985 469 185]
[131 805 349 671 681 793 356 31 29 396]
[462 433 587 180 529 618 676 567 695 612]
[682 862 827 947 971 152 345 37 628 523]
[464 709 267 910 836 245 750 578 187 526]
[800 907 651 837 683 840 275 362 391 123]
[860 161 912 305 234 612 917 32 162 457]
[422 762 171 413 94 454 642 87 982 146]
[740 597 544 900 56 707 914 192 911 563]
[521 818 506 104 469 284 199 192 298 723]
[418 207 418 385 974 641 367 768 539 701]
[822 765 409 355 529 22 678 33 796 743]
[238 804 746 592 714 141 419 370 116 675]
[291 54 887 619 237 12 76 91 792 893]
[199 821 862 800 392 73 585 287 491 704]
[303 52 80 799 233 986 651 216 737 801]
[ 5 704 387 346 810 579 325 661 763 802]
[520 231 421 182 102 511 819 531 243 726]
[703 419 431 122 292 598 394 786 701 475]
[630 724 302 541 568 814 401 990 498 875]
[345 464 405 949 90 342 841 274 681 378]
[401 590 670 52 33 308 929 131 292 402]
[617 589 50 440 19 181 509 287 285 73]
[976 636 57 529 368 745 553 709 229 650]
[140 359 619 747 411 666 134 640 318 460]
[758 910 285 935 955 104 757 708 349 209]
[739 528 478 190 924 106 93 439 498 767]
[758 712 734 681 860 435 230 850 530 848]
[901 14 885 531 86 950 626 378 206 779]]
(32, 10, 64)
Process finished with exit code 0
6.2. tf.keras.layers.Embedding 函数传入权重在TF2.x 中
weight : 如果你要已经训练好的词向量,可以在这里传入。比如现在大部分用Google的Word2Vector中词向量。
import tensorflow as tf
import numpy as np
weight = np.arange(60).reshape(10, 6)
for i in range(10):
weight[i] = i
print(weight)
model = tf.keras.Sequential()
model.add(tf.keras.layers.Embedding(10, 6, input_length=2, weights =[weight]))
input_array = np.random.randint(10, size=(3, 2))
print(input_array)
model.compile('rmsprop', 'mse')
output_array = model.predict(input_array)
print(output_array.shape)
print(output_array)
执行结果
10
[[0 0 0 0 0 0]
[1 1 1 1 1 1]
[2 2 2 2 2 2]
[3 3 3 3 3 3]
[4 4 4 4 4 4]
[5 5 5 5 5 5]
[6 6 6 6 6 6]
[7 7 7 7 7 7]
[8 8 8 8 8 8]
[9 9 9 9 9 9]]
[[7 8]
[3 1]
[2 0]]
(3, 2, 6)
[[[7. 7. 7. 7. 7. 7.]
[8. 8. 8. 8. 8. 8.]]
[[3. 3. 3. 3. 3. 3.]
[1. 1. 1. 1. 1. 1.]]
[[2. 2. 2. 2. 2. 2.]
[0. 0. 0. 0. 0. 0.]]]
7. 参考资料
https://www.cnblogs.com/gaofighting/p/9625868.html
https://www.tensorflow.org/api_docs/python/tf/keras/layers/Embedding?version=nightly
https://blog.csdn.net/hit0803107/article/details/98377030
