graph embedding(图嵌入)
graph embedding(图嵌入)
文章目录
- graph embedding(图嵌入)
- 一、 什么是图嵌入(graph embedding)?
- 二、优点
- 三、方法
-
- 1、节点嵌入方法
- 2、图嵌入方法(整个图)
一、 什么是图嵌入(graph embedding)?
图嵌入是一种将图数据(通常为高维稀疏的矩阵)映射为低微稠密向量的过程,如图。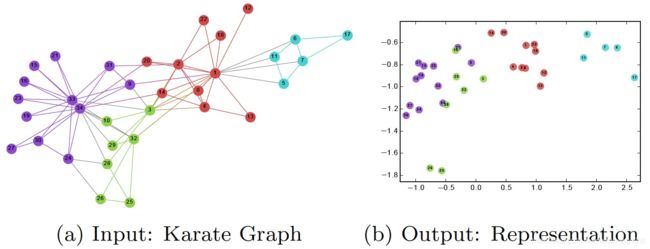
图嵌入需要捕捉到图的拓扑结构,顶点与顶点的关系,以及其他的信息 (如子图,连边等)。如果有更多的信息被表示出来,那么下游的任务将会获得更好的表现。在嵌入的过程中存在着一种共识:向量空间中保持连接的节点彼此靠近。基于此,研究者提出了拉普拉斯特征映射(Laplacian Eigenmaps)和局部线性嵌入(Locally Linear Embedding ,LLE)。
总的来说图嵌入技术大致可以分为两种:节点嵌入和图嵌入。当需要对节点进行分类,节点相似度预测,节点分布可视化时一般采用节点的嵌入;当需要在图级别(graph-level)上进行预测或者整个图结构预测,需要将整个图表示为一个向量进行嵌入表示。
二、优点
图是一种易于理解的表示形式,除此之外出于下面的原因需要对图进行嵌入表示:
- 在graph上直接进行机器学习具有一定的局限性,我们都知道图是由节点和边构成,这些向量关系一般只能使用数学,统计或者特定的子集进行表示,但是嵌入之后的向量空间具有更加灵活和丰富的计算方式。
- 图嵌入能够压缩数据, 我们一般用邻接矩阵描述图中节点之间的连接。 连接矩阵的维度是|V| x |V|,其中|V|
是图中节点的个数。矩阵中的每一列和每一行都代表一个节点。矩阵中的非零值表示两个节点已连接。将邻接矩阵用用大型图的特征空间几乎是不可能的。一个具有1M节点和1Mx1M的邻接矩阵的图该怎么表示和计算呢?但是嵌入可以看做是一种压缩技术,能够起到降维的作用。 - 向量计算比直接在图上操作更加的简单、快捷
但是图嵌入也需要满足一定的要求
- 属性选择:确保嵌入能够很好地描述图的属性,即需要表示图拓扑,节点连接和节点邻域。这样后期的预测或可视化才能获得较好的表现。
- 可扩展性:大多数真实网络都很大,包含了大量节点和边。嵌入方法应具有可扩展性,能够处理大型图。定义一个可扩展的模型具有挑战性,尤其是当该模型旨在保持网络的全局属性时。网络的大小不应降低嵌入过程的速度,一个好的嵌入方法不仅在小图上高效嵌入,同时也需要在大图上能够高效地嵌入。
- 嵌入的维度:实际嵌入时很难找到表示的最佳维数,维度越大能够保留的信息越多,但是通常有更高的时间和空间复杂度。较低的维度虽然时间、空间复杂度低,但无疑会损失很多图中原有的信息
三、方法
1、节点嵌入方法
- DeepWalk
在由物品组成的图结构上进行随机游走,产生大量物品序列,然后将这些物品序列作为训练样本输入word2vec进行训练,得到物品的embedding
DeepWalk通过随机游走(truncated random walk)学习出一个网络的表示,在网络标注顶点很少的情况也能得到比较好的效果。随机游走起始于选定的节点,然后从当前节点移至随机邻居,并执行一定的步数,该方法大致可分为三个步骤:
- 采样:通过随机游走对图上的节点进行采样,在给定的时间内得到一个节点构成的序列,论文研究表明从每个节点执行32到64次随机遍历就足够表示节点的结构关系;
- 训练skip-gram:随机游走得到的节点序列与word2vec方法中的句子相当。文本中skip-gram的输入是一个句子,在这里输入为随机游走采样得到的序列,进一步通过最大化预测相邻节点的概率进行预测周围节点进行训练和学习。
通常预测大约20个邻居节点-左侧10个节点,右侧10个节点。 - 计算嵌入

DeepWalk通过随机游走去可以获图中点的局部上下文信息,因此学到的表示向量反映的是该点在图中的局部结构,两个点在图中共有的邻近点(或者高阶邻近点)越多,则对应的两个向量之间的距离就越短。但是DeepWalk方法随机执行随机游走,这意味着嵌入不能很好地保留节点的局部关系,Node2vec方法可以解决此问题。
- Node2vec
Node2vec是DeepWalk的改进版,定义了一个bias random walk的策略生成序列,仍然用skip gram去训练。
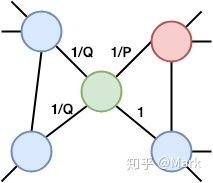
该算法引入了参数P和Q,参数Q关注随机游走中未发现部分的可能性,即控制着游走是向外还是向内: 若Q>1,随机游走倾向于访问接近的顶点(偏向BFS); 若Q<1,倾向于访问远离的顶点(偏向DFS)。
参数P控制了随机游走返回到前一个节点的概率。也就是说,参数P控制节点局部关系的表示,参数Q控制较大邻域的关系。
- SDNE
SDNE没有采用随机游走的方法而是使用自动编码器来同时优化一阶和二阶相似度,学习得到的向量表示保留局部和全局结构,并且对稀疏网络具有鲁棒性。一阶相似度表征了边连接的成对节点之间的局部相似性。 如果网络中的两个节点相连,则认为它们是相似的。 举个例子:当一篇论文引用另一篇论文时,意味着它们很可能涉及相似的主题,如6和7。但是当两个节点不相连时如5和6,他们就不具有相似度了吗?显然不是,从图上可以看出来他们虽然没有直接连接,但是他们有共同的邻居1,2,3,4,那么这时候就需要用二阶相似度来衡量了。
二阶相似度表示节点邻域结构的相似性,它能够了表征全局的网络结构。 如果两个节点共享许多邻居,则它们趋于相似。
SDNE的具体做法是使用自动编码器来保持一阶和二阶网络邻近度。它通过联合优化这两个近似值来实现这一点。该方法利用高度非线性函数来获得嵌入。模型由两部分组成:无监督和监督。前者包括一个自动编码器,目的是寻找一个可以重构其邻域的节点的嵌入。后者基于拉普拉斯特征映射,当相似顶点在嵌入空间中彼此映射得很远时,该特征映射会受到惩罚
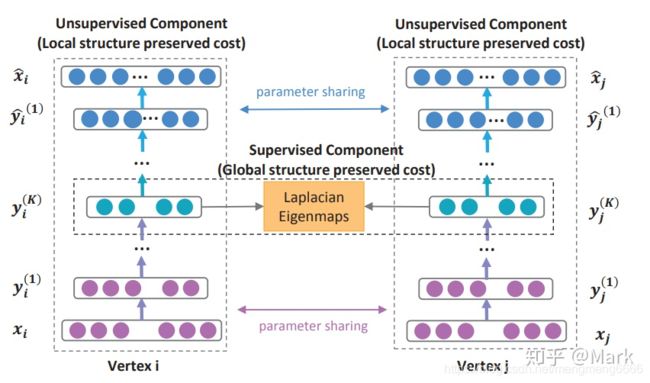
D. Wang, P. Cui, W. Zhu, Structural Deep Network Embedding (2016), Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining提出的模型由无监督部分与监督部分两部分组成。无监督部分用于提取与二阶估计相关的特征;同时由于部分节点是直接相连的,因而可以得到其的一阶估计,从而引入模型的有监督部分。这两部分的损失函数线性组合,联合优化
- EGES(阿里2018)
基本思想:在Deepwalk上生成的图embedding基础上引入补充信息,解决冷启动问题,使没有历史行为记录的的商品获得合理的初始embedding - LINE
2、图嵌入方法(整个图)
整个图嵌入的方式中具有代表性的方法:graph2vec
图嵌入是将整个图用一个向量表示的方法,Graph2vec【5】同样是基于skip-gram思想,把整个图编码进向量空间, 类似文档嵌入doc2vec, doc2vec在输入中获取文档的ID,并通过最大化文档预测随机单词的可能性进行训练。

Graph2vec由三个步骤构成
-
采样并重新标记图中的所有子图。子图是出现在所选节点周围的一组节点。子图中的节点距离所选边数不远。
-
训练skip-gram模型。 类似于文档doc2vec,由于文档是单词集,而图是子图集,在此阶段,对skip-gram模型进行训练。经过训练,可以最大程度地预测输入中存在于图中的子图的概率。

-
通过在输入处提供子图的id索引向量来计算嵌入
参考:
https://zhuanlan.zhihu.com/p/87572912
《深度学习推荐系统》