支持向量机实现鸢尾花数据集分类matlab
问题描述:
在进行感知机,以及逻辑斯蒂回归问题的讨论中,我们都以二分类问题为例。其中对于线性不可分的数据集,感知机和逻辑斯蒂回归已然失效,逻辑斯蒂回归对感知机进行的优化,是进行了一种思维上的“偷懒”,不再武断地判断预测数据属于哪个类,而是“圆滑”地告诉我们该数据属于哪一个的概率多大,通过对极大似然函数的参数估计,实现了模型的学习;通过极大似然估计,实现了数据类别的预测。但是这种优化并没有对线性不可分数据集提出解决方法,支持向量机,运用了几何间隔最大化(硬间隔或软间隔)和核技巧,将问题通过拉格朗日对偶转化,“投靠”了更高维的空间,即将线性不可分的数据集通过核技巧映射到高维空间(事实上,支持向量机并没有直接将空间进行映射,而是通过核技巧将内积进行从欧氏空间到希尔伯特空间的转换),企图从高维空间找到一个超平面能将数据集正确分类。
直观思路:
该思路的比较直观的解释,如果我们利用有限的特征不能将事物分类,那么我们可以将这些有限的特征通过某些关系组合构成新的特征从而识别出某类事物。如图1是原始数据集在某平面的映射,可见它是线性不可分的,我们通过
图1 拥有两个特征的数据集
核技巧可以将其“映射”到高维空间,我们猜想在高维空间这个数据集是线性可分的,于是得到图2,重新映射后,发现可以进行线性分类。
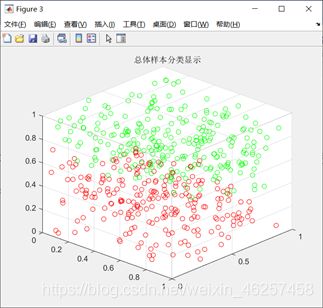
图2 三维空间的映射
图3 重新找到一个平面进行映射
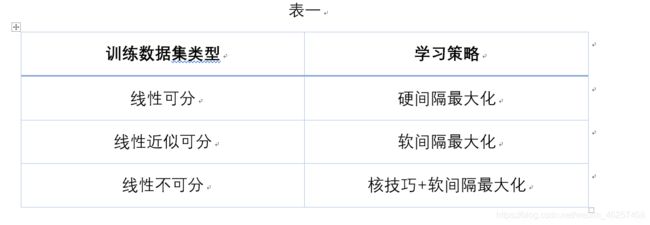
适用范围:
二分类模型,属于非线性分类器,策略为间隔最大化。
对于数据集不同的情况,采取的学习策略也不同。
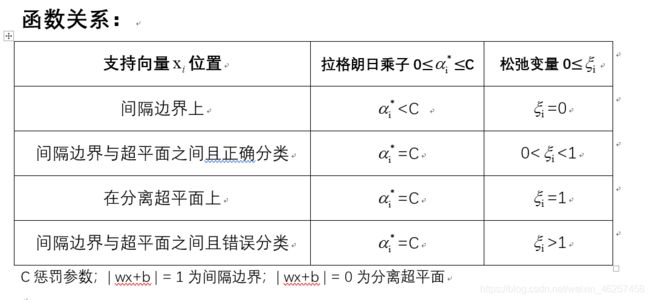
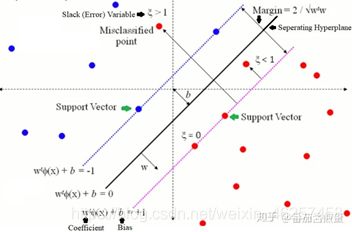
直观理解:如果一个样例点靠近我们的超平面,我们将它对应的 增大,类似于惩罚,为了使松弛变量发挥作用,设置一个惩罚参数,作为上界, 如果大于这个参数则均取得这个参数,以便于让松弛项发挥作用。当松弛变量 =0,则说明不需要进行软约束既满足正确分类且满足硬间隔最大化,样例在间隔边界上;当松弛变量增大,说明该样例已经进入了两个间隔之间,松弛变量的数值越大,则说明我们需要对这个样采取更放松的条件,当放松的条件超过某个值,即 >1,说明该样例已经被目前的超平面错误分类。
待续。。。
概念补充:
关于“凸”

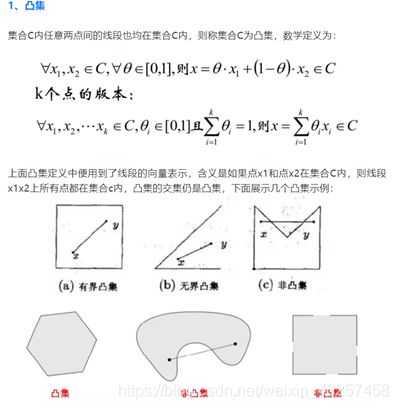

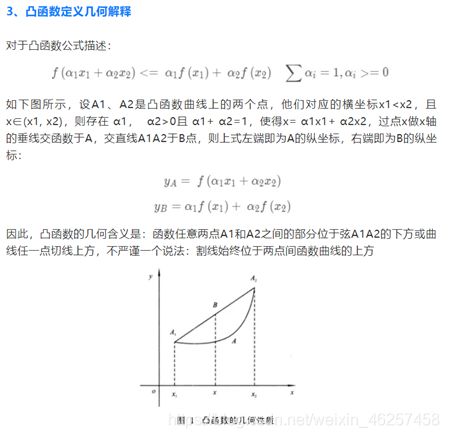

实例运行:
预先准备了数据集,数据为随机生成,并且根据预设的函数关系(为验证SVM的有效性,采用了非线性的函数关系),进行了分类。
使用了线性可分以及线性不可分的数据集对不同的核函数进行测试和验证,以下为测试结果。

图 5 线性核函数

图 6 线性核函数准确率

图 9 sigmoid核函数

图 10 sigmoid核函数准确率
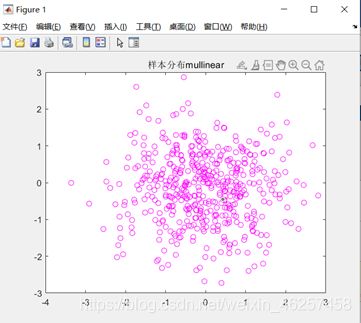
图 11 多项式核函数
线性不可分数据集:
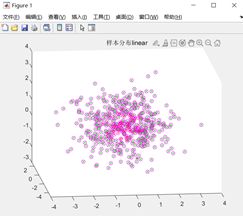
图 13 线性核函数

图 14 线性核函数准确率
结论:
由上不难看出,对于线性可分的数据集,线性核函数表现良好,但多项式核函数表现欠佳;但对于线性不可分数据集,则情况相反。高斯核函数对于两种情况表现都比较好,这说明高斯核函数对于空间映射更具有普适性。
基于支持向量机的多分类问题:
方法一:One-Versus-Rest(一对多)
训练时依次把某个类别的样本归为一类,其他剩余的样本归为另一类,这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。
优点:
分类速度快,分离超平面个数为数据类别数。缺点:存在分类重叠与不可分类现象。
分类重叠现象:
在进行测试时,对于每一类label,svm模型都会选择说测试数据属于这一类,导致都想“争抢”测试样本;此类问题比较容易解决,选择一个置信度最高的类即可(几何间隔最大)。
不可分类现象:
在进行测试时,对于每一类label,svm都会说不属于自己这一类,导致都选择“排斥”测试样本,这导致多分类svm失效。
数据集偏斜现象:
训练集本身,对于每一类样本数据个数不对等,相差较多的情况,这样学得的超平面,为了保证间隔最小,会导致让小数据类别更多地被误分类,这是不难理解的,因为牺牲小部分样例误分类如果可以让大数目样本更多的被正确分类,这种牺牲对于损失函数下降是有意义的,从而导致在测试时本属于小数目样本的数据可能被误分类为大数目的样本类别中。One-Versus-Rest 方案正是人为的造成了数据集偏斜。
方法二:One-Versus-One(一对一)
具体做法是在任意两类样本之间设计一个SVM,因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。在训练时往往比一对多花的时间少,并且由于采用了投票表决的方式,一定程度上解决了样本不可分问题,但是分类的类别多的时候,会使svm数目爆炸。
方法三:Directed Acyclic Graph SVM(有向无环图)DAG SVM
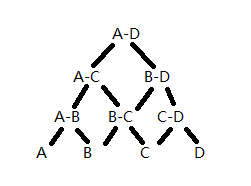
DAG存在的一个问题是单分类器的误判代价较高。如上图若根分类器判断错误,输入真实类别为A,却被错分至右边,这次误判将直接导致输入不会被正确分类。故而在选择根分类器时需选择鲁棒性较强的一个二分类器,子树的根分类器同理。
方法四:层次支持向量机
待续。。。
参考:
机器学习中对核函数的理解:
https://link.zhihu.com/?target=http%3A//mp.weixin.qq.com/s%3F__biz%3DMzIxNDIwMTk2OQ%3D%3D%26mid%3D2649077019%26idx%3D1%26sn%3De0c4a6c502e3668e1dc410f21e531cfd%26scene%3D0%23wechat_redirect
核函数的定义和作用是什么?:
https://www.zhihu.com/question/24627666
机器学习概念篇:一文详解凸函数和凸优化,干货满满
https://mp.weixin.qq.com/s?src=11×tamp=1619016438&ver=3022&signature=vq2-rqI8DivdbDhKDqFMHs3Pc7uV-eZr3yWYxWxlMdktd4m4tTrA5q0X8I8GwZbo8QcFZKWWU5X1sakYzBPFviW7siF48zmFxf-ww-RF4AX5eaINFwM2tRxmQS*FfJ&new=1
拉格朗日对偶性
https://zhuanlan.zhihu.com/p/45431511
线性可分支持向量机推广到线性不可分(四)
https://zhuanlan.zhihu.com/p/42773288
机器学习-白板推导系列(七)-核方法(Kernel Method)笔记
https://zhuanlan.zhihu.com/p/337498283
支持向量机SVM—实现多分类问题的解决方案
https://blog.csdn.net/weixin_44822636/article/details/110820652
算法原理代码
%% 样本准备
close;clear;clc;data_features = 3;
[train_data,train_label,test_data,test_label,m1,n1,m2,n2] = data_build(1000,data_features,0.5);
%% 模型训练
Kernel = 'mullinear';% Kernel 核技巧备选:gaussian linear sigmoid mullinear triangle
svm = train_svm(train_data',train_label',Kernel,10); % svm = train_svm(X,Y,kertype,C) C为变量上界(惩罚因子) svm为结构体
%% 模型测试
result = test_svm(svm,test_data',test_label',Kernel);
fprintf('训练完成!\n应用模型:SVM 支持向量机\n优化算法:interior-point-convex\n核函数:%s\n测试集识别率为:%f\n',Kernel,result.accuracy);
%% 作图显示数据以及训练结果;中间为支持向量[二维]
draw_svm(train_data,train_label,svm,data_features,Kernel);
function [train_data,train_label,test_data,test_label,m1,n1,m2,n2] = data_build(data_num,data_features,k)
% [train,test] = data_build(data_num,data_features,k)
% 功能:生成数据并实现训练集和测试集分类
% 语法和参数列表:
% [train_data,train_label,test_data,test_label,m1,n1,m2,n2] = data_build(data_num,data_features,k)
% input:
% data_num -- 数据总量
% data_features -- 特征维数
% k -- 用于训练的比例
%
% output:
% 返回训练集与测试集的数据及标签(类别)
% 名称一一对应不再注释
% m1,n1,m2,n2分别为train_data,test_data的行列数
data = randn(data_num,data_features);
label = zeros(data_num,1);
for i = 1:data_num
% 根据数据特征数目设置分类依据
if data_features == 2
% if data(i,1)^2+data(i,2)^2 > 1
if data(i,1)+data(i,2) > 1
label(i)=1;
else
label(i)=-1;
end
elseif data_features > 2
if data(i,1)^2+data(i,2)^2+data(i,3)^2 < 1
label(i)=1;
else
label(i)=-1;
end
end
end
% 乱序排列
randIndex = randperm(data_num);
data_new=data(randIndex,:);
label_new=label(randIndex,:);
k = k*data_num;
train_data=data_new(1:k,:);
train_label=label_new(1:k,:);
test_data=data_new(k+1:end,:);
test_label=label_new(k+1:end,:);
[m1,n1] = size(train_data);
[m2,n2] = size(test_data);
end
function draw_svm(train_data,train_label,svm,data_features,Kernel)
% 功能说明:根据数据特征的维数判断,进而分别绘图
% 函数语法及参数列表:draw_svm(inputArg1,data_features)
% input:
% train_data: 训练数据集
% train_label:训练集数据的类别
% svm:svm结构体(详见train_svm,help train_svm)
% data_features特征维数
switch data_features
case 2
plot(train_data(train_label==1,1),train_data(train_label==1,2),'ro',train_data(train_label==-1,1),train_data(train_label==-1,2),'go');hold on;
plot(svm.data(1,:),svm.data(2,:),'mo');hold on;title(['样本分布',Kernel]); % 显示支持向量 'mo'品红色的圈
otherwise
plot3(train_data(train_label==1,1),train_data(train_label==1,2),train_data(train_label==1,3),'r.');hold on;
plot3(train_data(train_label==-1,1),train_data(train_label==-1,2),train_data(train_label==-1,3),'gx');hold on;
plot3(svm.data(1,:),svm.data(2,:),svm.data(3,:),'mo');hold on;
title(['样本分布',Kernel]);
end
end
function K = kernel(X,Y,kerneltype)
% 功能:支持多种核运算;
% 语法结构:K = kernel(X,Y,kerneltype),kerneltype选择核技巧
% 'linear':线性内积
% K(v1,v2) = <v1,v2>
% 'gaussian':高斯核 %
% K(v1,v2)=exp(-gama||v1-v2||^2)
% 'sigmoid':sigmoid核;双曲正切函数
% K(v1,v2)=tanh(gama<v1,v2>+c)
% 'mullinear':多项式核
% K(v1,v2)=<v1,v2>^d;d为多项式的次数
% 'triangle':三角核
% K(v1,v2)=-||v1-v2||^d
% 在svm中运用线性,高斯或者sigmoid效果比较好
switch kerneltype
case 'linear' % 线性内积
K = X'*Y;
case 'sigmoid'
belta = 0.01;
theta = 0.001;
K = tanh(belta*X'*Y+theta);
case 'gaussian'% k(v1,v2) = exp(-||v1-v2||^2/(2sigma^2))
delta = 2*1.414;
delta = delta*delta;
XX = sum(X'.*X',2);
YY = sum(Y'.*Y',2);
XY = X'*Y;
K = abs(repmat(XX,[1 size(YY,1)]) + repmat(YY',[size(XX,1) 1]) - 2*XY);
K = exp(-K./delta);
case 'mullinear'
K = (X'*Y).^2;
% case'triangle'
% K = -norm(X-Y,1)^2;
end
end
function result = test_svm(svm, test_data, test_label, kerneltype)
% 功能说明:
% 完成测试集的预测以及准确率的输出
% 语法习惯核参数列表:result = test(svm, test_data, test_label, kerneltype)
% input:
% svm: train_svm函数返回的结构体(详见help train_svm)
% test_data: 测试数据
% test_label:测试集标签
% kerneltype:核技巧种类,形式参数,可选:linear gaussian sigmoid mullinear triangle
% output:
% result:结构体,属性如下
% result.Y:测试集中数据的预测类别 result.Y ∈{+1,-1}
% result.accuracy:测试集的准确率
% 教材非线性支持向量机学习算法的策略为选择a的一个正分量0< a <C进行计算
% 此处选择了对所有满足0< ai <C求得bi,并对b进行取平均运算
sum_b = svm.label - (svm.a'.* svm.label)*kernel(svm.data,svm.data,kerneltype);
b = mean(sum_b);
w = (svm.a'.* svm.label)*kernel(svm.data,test_data,kerneltype);% 统一起见,令 w = sigma(ai*yi*K(x,xi)
result.Y = sign(w+b);% 加外壳符号函数进行分类
result.accuracy = size(find(result.Y==test_label))/size(test_label);% 预测正确的数据数目/总测试集数目
end
function svm = train_svm(train_data,train_label,kertype,C)
% 功能说明:完成SVM训练
% 语法习惯与参数列表:svm = train_svm(train_data,train_label,kertype,B)
% input:
% train_data:训练数据
% train_label:训练数据的类别
% kertype:核函数的类别
% C 惩罚参数
% B 为变量约束中的上界
% output:
% svm:是一个结构体,包含属性如下:
% svm.a :得到的凸二次规划的解
% svm.data : 支持向量
% svm.label :支持向量的类别
% ------------*************************···········
% ------------关键函数quadprog的一些说明···········
% 函数quadprog:用于解二次规划问题
% 问题描述:
% min(x): 0.5·x'·H·x + f'·x
%
% A·x <= b,
% s.t.: Aeq·x = beq;
% lb <=x <= ub;
%
% 全参数语法结构:x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);
% 变量说明:
% H,A,Qeq是矩阵,f,b,beq,lb,ub,x是向量
% options:选择优化算法并进行设置
% 优化选项设置,对属性进行设置:
% 使用 optimoptions 或 optimset 创建选项(属性);
% 指定为 optimoptions 的输出或 optimset 等返回的结构体。
% 变量初始化以及超参设置
n = length(train_label); % 对变量的自由约束,上下界
H = (train_label'*train_label).*kernel(train_data,train_data,kertype);% H为yi*yj*K(xi,xj)
f = -ones(n,1); % 保证f为列向量,原式中包含转置操作
A = [];% 不含不等约束
b = [];% 不含不等约束
Aeq = train_label; % s.t.: aY = 0;
beq = 0; % s.t.: aY = 0;
lb = zeros(n,1); % 解:a 的范围
ub = C*ones(n,1); % 0 <= a <= C
a0 = zeros(n,1); % a0是解的初始近似值
options = optimset; % 'interior-point-convex'(默认优化算法)
options.Display = 'iter-detailed';% 显示优化步骤
% x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) 使用 options 中指定的优化选项求解上述问题。
% 使用 optimset 创建 options。如果不提供初始点,设置 x0 = []。
a = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
% 寻找支持向量;a>e 则认为train_data为支持向量 函数find查找逻辑为真的索引
e = 1e-4;
sv_index = find(abs(a)>e);
svm.a = a(sv_index);
svm.data = train_data(:,sv_index);% 作图显示支持向量位置
svm.label = train_label(sv_index);
end
鸢尾花数据集SVM实战
一 数据集信息:
··是一个很小的数据集,仅有150行,5列,每类有50个数据。该数据集的四个特征属性的取值都是数值型的,他们具有相同的量纲,不需要做任何标准化的处理,第五列为通过前面四列所确定的鸢尾花所属的类别名称。
·数据集处理:为了增加实验的科学性,随机将样本打乱了顺序,进行重新排列。
二 2分类(基于前两个特征):
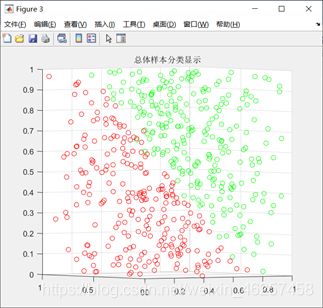
首先完成课程的任务,即根据前一百条数据的前两个特征完成学习,进行对鸢尾花的有效分类,并标注支持向量以及分离超平面效果如图2-1,图中红色与绿色代表正负样例,品红色为支持向量,直线为分离超平面。
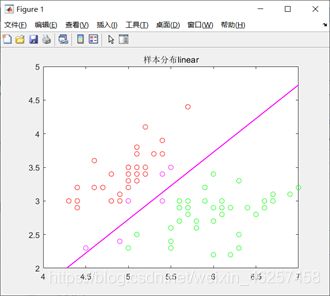
图2-1 基于前一百个样本两个特征的分类
为了演示方便(主要是为了在图中显示更多的样例),在这里我选取了0.8 : 0.2的样本比例分别用于训练和测试,采用核函数为’linear’ ( 公式见式2.1 ) 由于鸢尾花数据集为线性可分的,准确率达到了百分之百,降低训练测试比到 0.5 : 0.5之后,准确率如图2-2,仍为百分之百。

图2-2 识别准确率

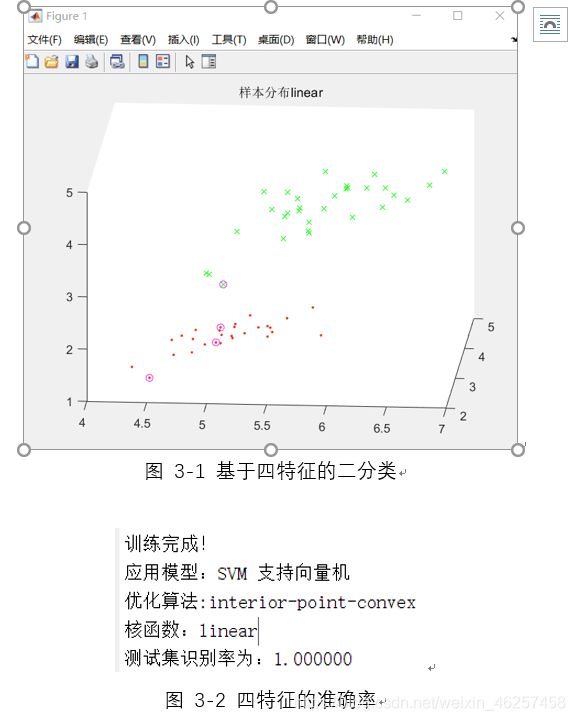
三 2分类(基于四个特征):
对于依靠前两个特征,已经能够将 ‘setosa’ 'versicolor’两类正确分类,现尝试利用四个特征对其进行分类,来验证在有冗余分类特征的前提下,支持向量机是否还能应对。采用核函数仍然为’linear’,结果如图3-1,准确率如图3-2,增加数据特征维数之后,表现仍然良好,这是容易解释的,因为鸢尾花数据集本身就是线性可分的。
参考:
鸢尾花(iris)数据集
https://www.gairuo.com/p/iris-dataset
代码
%% 数据预处理和导入
close;clear;clc
[train_data,train_label,test_data,test_label,m1,n1,m2,n2] = data_set(0.6,100);
%% 模型训练
Kernel = 'linear';% Kernel 核技巧备选:gaussian linear sigmoid mullinear
svm = train_svm(train_data',train_label',Kernel,10); % svm = train_svm(X,Y,kertype,C) C为变量上界(惩罚因子) svm为结构体
%% 模型测试
result = test_svm(svm,test_data',test_label',Kernel);
fprintf('训练完成!\n应用模型:SVM 支持向量机\n优化算法:interior-point-convex\n核函数:%s\n测试集识别率为:%f\n',Kernel,result.accuracy);
%% 作图显示数据以及训练结果;中间为支持向量[三维]
draw_svm(train_data,train_label,svm,3,Kernel);
function [train_data,train_label,test_data,test_label,m1,n1,m2,n2] = data_set(k,data_num)
% 功能说明:完成数据的预处理,setosa:1 versicolor:2 virginica:3
% 调用语法及参数说明:[data_iris,data_label] = data_set();
%
load('data_iris.mat');load('data_label.mat');
data_label = zeros(data_num,1);
for i = 1:data_num
switch species(i)
case 'setosa'
data_label(i) = 1;
case 'versicolor'
data_label(i) = -1;
% case 'virginica'
% data_label(i) = 3;
end
end
data_iris = iris(1:data_num,:);
% 乱序排列
randIndex = randperm(data_num);
data_new=data_iris(randIndex,:);
label_new=data_label(randIndex,:);
% 分为两组,比例k用于训练,剩余用于测试
k = k*data_num;
train_data=data_new(1:k,:);
train_label=label_new(1:k,:);
test_data=data_new(k+1:end,:);
test_label=label_new(k+1:end,:);
[m1,n1] = size(train_data);
[m2,n2] = size(test_data);
end
function draw_svm(train_data,train_label,svm,data_features,Kernel)
% 功能说明:根据数据特征的维数判断,进而分别绘图
% 函数语法及参数列表:draw_svm(inputArg1,data_features)
% input:
% train_data: 训练数据集
% train_label:训练集数据的类别
% svm:svm结构体(详见train_svm,help train_svm)
% data_features特征维数
switch data_features
case 2
plot(train_data(train_label==1,1),train_data(train_label==1,2),'ro',train_data(train_label==-1,1),train_data(train_label==-1,2),'go');hold on;
plot(svm.data(1,:),svm.data(2,:),'mo');hold on;title(['样本分布',Kernel]); % 显示支持向量 'mo'品红色的圈
[x1,x2] = meshgrid(4:0.01:7,2:0.01:5);
[rows,cols] = size(x1);
nt = rows*cols;
Xt = [reshape(x1,1,nt);reshape(x2,1,nt)];
Yt = ones(1,nt);
result = test_svm(svm, Xt, Yt,Kernel);
Yd = reshape(result.Y,rows,cols);
contour(x1,x2,Yd,'m');
otherwise
plot3(train_data(train_label==1,1),train_data(train_label==1,2),train_data(train_label==1,3),'r.');hold on;
plot3(train_data(train_label==-1,1),train_data(train_label==-1,2),train_data(train_label==-1,3),'gx');hold on;
plot3(svm.data(1,:),svm.data(2,:),svm.data(3,:),'mo');hold on;
title(['样本分布',Kernel]);
end
end
function K = kernel(X,Y,kerneltype)
% 功能:支持多种核运算;
% 语法结构:K = kernel(X,Y,kerneltype),kerneltype选择核技巧
% 'linear':线性内积
% K(v1,v2) = <v1,v2>
% 'gaussian':高斯核 %
% K(v1,v2)=exp(-gama||v1-v2||^2)
% 'sigmoid':sigmoid核;双曲正切函数
% K(v1,v2)=tanh(gama<v1,v2>+c)
% 'mullinear':多项式核
% K(v1,v2)=<v1,v2>^d;d为多项式的次数
% 'triangle':三角核
% K(v1,v2)=-||v1-v2||^d
% 在svm中运用线性,高斯或者sigmoid效果比较好
switch kerneltype
case 'linear' % 线性内积
K = X'*Y;
case 'sigmoid'
belta = 0.01;
theta = 0.001;
K = tanh(belta*X*Y+theta);
case 'gaussian'% k(v1,v2) = exp(-||v1-v2||^2/(2sigma^2))
delta = 2*1.414;
delta = delta*delta;
XX = sum(X'.*X',2);
YY = sum(Y'.*Y',2);
XY = X'*Y;
K = abs(repmat(XX,[1 size(YY,1)]) + repmat(YY',[size(XX,1) 1]) - 2*XY);
K = exp(-K./delta);
case 'mullinear'
K = (X'*Y).^2;
% case'triangle'
% K = -norm(X-Y,1)^2;
end
end
function result = test_svm(svm, test_data, test_label, kerneltype)
% 功能说明:
% 完成测试集的预测以及准确率的输出
% 语法习惯核参数列表:result = test(svm, test_data, test_label, kerneltype)
% input:
% svm: train_svm函数返回的结构体(详见help train_svm)
% test_data: 测试数据
% test_label:测试集标签
% kerneltype:核技巧种类,形式参数,可选:linear gaussian sigmoid mullinear triangle
% output:
% result:结构体,属性如下
% result.Y:测试集中数据的预测类别 result.Y ∈{+1,-1}
% result.accuracy:测试集的准确率
% 教材非线性支持向量机学习算法的策略为选择a的一个正分量0< a <C进行计算
% 此处选择了对所有满足0< ai <C求得bi,并对b进行取平均运算
sum_b = svm.label - (svm.a'.* svm.label)*kernel(svm.data,svm.data,kerneltype);
b = mean(sum_b);
w = (svm.a'.* svm.label)*kernel(svm.data,test_data,kerneltype);% 统一起见,令 w = sigma(ai*yi*K(x,xi)
result.Y = sign(w+b);% 加外壳符号函数进行分类
result.plotx = min(test_data(1,:)):0.001: max(test_data(1,:));
result.accuracy = size(find(result.Y==test_label))/size(test_label);% 预测正确的数据数目/总测试集数目
end
function svm = train_svm(train_data,train_label,kertype,C)
% 功能说明:完成SVM训练
% 语法习惯与参数列表:svm = train_svm(train_data,train_label,kertype,B)
% input:
% train_data:训练数据
% train_label:训练数据的类别
% kertype:核函数的类别
% C 惩罚参数
% B 为变量约束中的上界
% output:
% svm:是一个结构体,包含属性如下:
% svm.a :得到的凸二次规划的解
% svm.data : 支持向量
% svm.label :支持向量的类别
% ------------*************************···········
% ------------关键函数quadprog的一些说明···········
% 函数quadprog:用于解二次规划问题
% 问题描述:
% min(x): 0.5·x'·H·x + f'·x
%
% A·x <= b,
% s.t.: Aeq·x = beq;
% lb <=x <= ub;
%
% 全参数语法结构:x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);
% 变量说明:
% H,A,Qeq是矩阵,f,b,beq,lb,ub,x是向量
% options:选择优化算法并进行设置
% 优化选项设置,对属性进行设置:
% 使用 optimoptions 或 optimset 创建选项(属性);
% 指定为 optimoptions 的输出或 optimset 等返回的结构体。
% 变量初始化以及超参设置
n = length(train_label); % 对变量的自由约束,上下界
H = (train_label'*train_label).*kernel(train_data,train_data,kertype);% H为yi*yj*K(xi,xj)
f = -ones(n,1); % 保证f为列向量,原式中包含转置操作
A = [];% 不含不等约束
b = [];% 不含不等约束
Aeq = train_label; % s.t.: aY = 0;
beq = 0; % s.t.: aY = 0;
lb = zeros(n,1); % 解:a 的范围
ub = C*ones(n,1); % 0 <= a <= C
a0 = zeros(n,1); % a0是解的初始近似值
options = optimset; % 'interior-point-convex'(默认优化算法)
options.Display = 'iter-detailed';% 显示优化步骤
% x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options) 使用 options 中指定的优化选项求解上述问题。
% 使用 optimset 创建 options。如果不提供初始点,设置 x0 = []。
a = quadprog(H,f,A,b,Aeq,beq,lb,ub,a0,options);
% 寻找支持向量;a>e 则认为train_data为支持向量 函数find查找逻辑为真的索引
e = 1e-4;
sv_index = find(abs(a)>e);
svm.a = a(sv_index);
svm.data = train_data(:,sv_index);% 作图显示支持向量位置
svm.label = train_label(sv_index);
end
注:
writer :M宝可梦
引用请注明出处,谢谢合作!
处理之后的数据集及完整代码见:
https://download.csdn.net/download/weixin_46257458/18477867