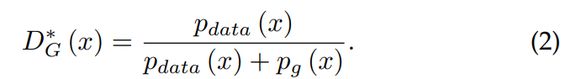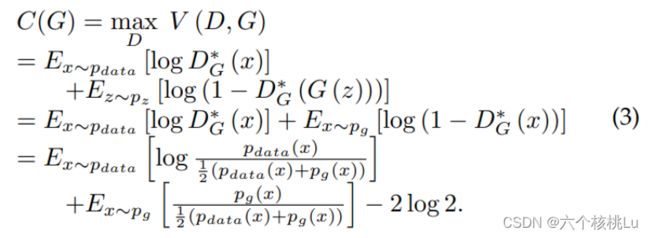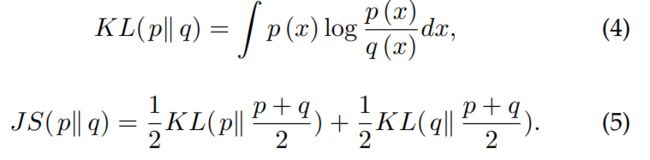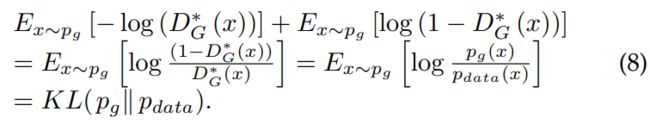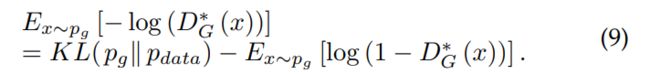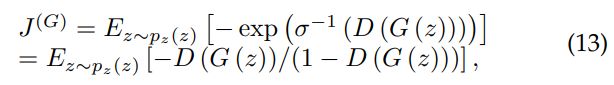生成对抗网络GAN 学习笔记

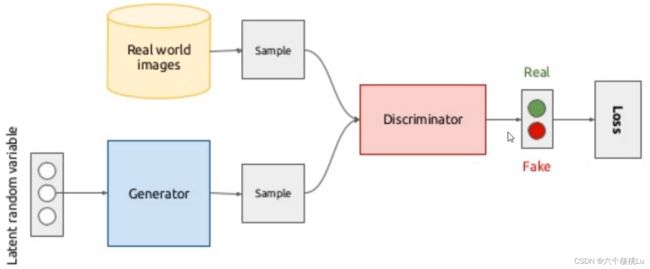
GAN由生成器和判别器组成：

        生成器（Generative Model）的本质也是一个神经网络，或者说是一个函数     G(x)

        判别器（Discriminative Model）的本质也是一个神经网络     D(x)

所以GAN的训练本质就是训练两个神经网络。

---

GAN 的算法原理

        1.最原始的极大极小博弈

        GAN的目标函数是

 其中 D(x) 是 [1, 0]^T 和 [D(x), 1 - D(x)]^T 间的交叉熵。类似地，log(1-D(G(z))) 是 [0, 1]^T 和 [D(G(z)), 1 - D(G(z))]^T 间的交叉熵。

        对于一个固定的 G，GAN中给出了最优的判别器 D：

 (1) 式中的极大极小博弈可以被重新形式化为：

两个概率分布 p(x) 和 q(x) 之间的 KL 散度和 JS 散度定义如下：

因此，(3) 式等价于

因此，GAN 的目标函数和 KL 散度与 JS 散度都相关。

        

        2.非饱和博弈

        实际上，公式 (1) 可能无法为 G 提供足够大的梯度使其很好地学习。一般来说，G 在学习过程的早期性能很差，产生的样本与训练数据有明显的差异。因此，D 可以以高置信度拒绝 G 生成的样本。在这种情况下，log(1-D(G(z))) 是饱和的。我们可以训练 G 以最大化 log(D(G(z)))，而非最小化 log(1-D(G(z)))。生成器的损失则变为：

        这个新的目标函数可以在训练过程中使 D 和 G 的达到相同的不动点，但是在学习初期就提供了大得多的梯度。非饱和博弈是启发式的，而非理论驱动的。然而，非饱和博弈还存在其它问题，如用于训练 G 的数值梯度不稳定。在最优的 下，有

因此 [-log((x))] 等价于

根据 (3) 式和 (6) 式，有

因此 [log^(1 - (x))] 等价于 

将 (11) 式代入 (9) 式，可以得到：

        从 (12) 式可以看出，对非饱和博弈中的替代 G 损失函数的优化是矛盾的，因为第一项目标是使生成的分布与实际分布之间的差异尽可能小，而由于负号的存在，第二项目标是使得这两个分布之间的差异尽可能大。这将为训练 G 带来不稳定的数值梯度。此外，KL 散度是非对称度量，这可以从以下两个例子中反映出来：

        对 G 的两种误差的惩罚是完全不同的。第一种误差是 G 产生了不真实的样本，对应的惩罚很大。第二种误差是 G 未能产生真实的样本，而惩罚很小。第一种误差是生成的样本不准确，而第二种误差是生成的样本不够多样化。基于这个原理，G 倾向于生成重复但是安全的样本，而不愿意冒险生成不同但不安全的样本，这会导致模式坍塌（mode collapse）问题。

        3.最大似然博弈

        在 GAN 中，有许多方法可以近似 (1) 式。假设判别器是最优的，想最小化

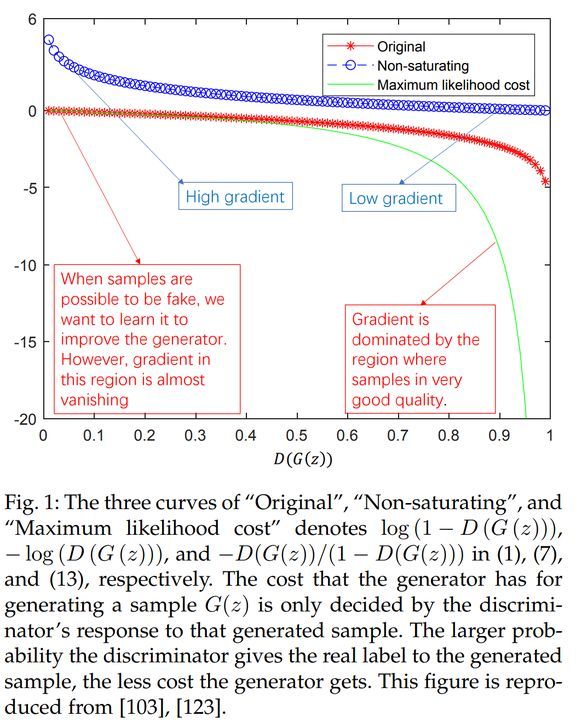
        下图展示了对于原始的极大极小博弈、非饱和博弈以及最大似然博弈的比较。

由上图  可以得到三个观察结果

        首先，当样本可能来自于生成器的时候，即在图的左端，最大似然博弈和原始极大极小博弈都受到梯度弥散的影响，而启发式的非饱和博弈不存在此问题。

        第二，最大似然博弈还存在一个问题，即几乎所有梯度都来自曲线的右端，这意味着每个 minibatch 中只有极少一部分样本主导了梯度的计算。这表明减小样本方差的方法可能是提高基于最大似然博弈的 GAN 性能的重要研究方向。

        第三，基于启发式的非饱和博弈的样本方差较低，这可能是它在实际应用中更成功的可能原因。

---

 

实例一 (有些问题 调试中......)

深度学习中经常看到epoch、iteration和batchsize，下面按照自己的理解说说这三个区别：

（1）batchsize：批大小。在深度学习中，一般采用SGD训练，即每次训练在训练集中取batchsize个样本训练；
（2）iteration：1个iteration等于使用batchsize个样本训练一次；
（3）epoch：1个epoch等于使用训练集中的全部样本训练一次；

举个例子，训练集有1000个样本，batchsize=10，那么：
训练完整个样本集需要：
100次iteration，1次epoch。

---

 实例二        学习手写数字

 采用 MNIST 数据集作为实验数据，最后看到生成器能够产生看起来像真的数字！

import numpy as np
import matplotlib.pyplot as plt
from keras.layers import Dense, Dropout, Input
from keras.models import Model, Sequential
from keras.datasets import mnist
from tqdm import tqdm
from keras.layers.advanced_activations import LeakyReLU
from keras.optimizers import Adam

# 导入数据
def load_data():
    (x_train, y_train), (x_test, y_test) = mnist.load_data()
    x_train = (x_train.astype(np.float32) - 127.5)/127.5

    # 将图片转为向量 x_train from (60000, 28, 28) to (60000, 784)
    # 每一行 784 个元素
    x_train = x_train.reshape(60000, 784)
    return (x_train, y_train, x_test, y_test)
(X_train, y_train,X_test, y_test)=load_data()
print(X_train.shape)

# 定义优化器
def adam_optimizer():
    return Adam(lr=0.0002, beta_1=0.5)

# 定义生成器：输入是 100 维，经过三层隐藏层，输出 784 维的向量（造假的图片）
def create_generator():
    generator=Sequential()
    generator.add(Dense(units=256,input_dim=100))
    generator.add(LeakyReLU(0.2))

    generator.add(Dense(units=512))
    generator.add(LeakyReLU(0.2))

    generator.add(Dense(units=1024))
    generator.add(LeakyReLU(0.2))

    generator.add(Dense(units=784, activation='tanh'))

    generator.compile(loss='binary_crossentropy', optimizer=adam_optimizer())
    return generator
g=create_generator()
g.summary()

# 定义判别器：判别器的输入为真实图片或者由生成器造出来的假图片（784维），经过三层隐藏层，输出类别（1 维）
def create_discriminator():
    discriminator = Sequential()
    discriminator.add(Dense(units=1024, input_dim=784))
    discriminator.add(LeakyReLU(0.2))
    discriminator.add(Dropout(0.3))

    discriminator.add(Dense(units=512))
    discriminator.add(LeakyReLU(0.2))
    discriminator.add(Dropout(0.3))

    discriminator.add(Dense(units=256))
    discriminator.add(LeakyReLU(0.2))

    discriminator.add(Dense(units=1, activation='sigmoid'))

    discriminator.compile(loss='binary_crossentropy', optimizer=adam_optimizer())
    return discriminator
d =create_discriminator()
d.summary()

# 定义生成对抗网络
def create_gan(discriminator, generator):
    discriminator.trainable=False
    # 这是一个链式模型：输入经过生成器、判别器得到输出
    gan_input = Input(shape=(100,))
    x = generator(gan_input)
    gan_output = discriminator(x)
    gan = Model(inputs=gan_input, outputs=gan_output)
    gan.compile(loss='binary_crossentropy', optimizer='adam')
    return gan
gan = create_gan(d,g)
gan.summary()

# 定义画图函数来可视化图片的生成
def plot_generated_images(epoch, generator, examples=100, dim=(10,10), figsize=(10,10)):
    noise = np.random.normal(loc=0, scale=1, size=[examples, 100])
    generated_images = generator.predict(noise)
    generated_images = generated_images.reshape(100, 28, 28)
    plt.figure(figsize=figsize)
    for i in range(generated_images.shape[0]):
        plt.subplot(dim[0], dim[1], i+1)
        plt.imshow(generated_images[i], interpolation='nearest')
        plt.axis('off')
    plt.tight_layout()
    plt.savefig('gan_generated_image %d.png' %epoch)
    plt.show()

# 生成对抗网络的训练函数
def training(epochs=1, batch_size=128):

    # 导入数据
    (X_train, y_train, X_test, y_test) = load_data()
    batch_count = X_train.shape[0] / batch_size

    # 定义生成器、判别器和GAN网络
    generator = create_generator()
    discriminator = create_discriminator()
    gan = create_gan(discriminator, generator)

    for e in range(1, epochs+1):
        print("Epoch %d" %e)
        for _ in tqdm(range(int(batch_count))):
            # 产生噪声喂给生成器
            noise = np.random.normal(0, 1, [batch_size, 100])

            # 产生假图片
            generated_images = generator.predict(noise)

            # 一组随机真图片
            image_batch =X_train[np.random.randint(low=0, high=X_train.shape[0], size=batch_size)]

            # 真假图片拼接
            X = np.concatenate([image_batch, generated_images])

            # 生成数据和真实数据的标签
            y_dis = np.zeros(2*batch_size)
            y_dis[:batch_size] = 0.9

            # 预训练，判别器区分真假
            discriminator.trainable = True
            discriminator.train_on_batch(X, y_dis)

            # 欺骗判别器 生成的图片为真的图片
            noise = np.random.normal(0, 1, [batch_size, 100])
            y_gen = np.ones(batch_size)

            # GAN的训练过程中判别器的权重需要固定
            discriminator.trainable = False

            # GAN的训练过程为交替“训练判别器”和“固定判别器权重训练链式模型”
            gan.train_on_batch(noise, y_gen)

        if e == 1 or e % 50 == 0:
            # 画图 看一下生成器能生成什么
            plot_generated_images(e, generator)

training(400,256)

1个epoch后 生成器生成的图片：

50个epoch后 生成器生成的图片：

 100个epoch后 生成器生成的图片：

 400个epoch后 生成器生成的图片：

---

REFERENCES：

https://arxiv.org/pdf/2001.06937.pdf

【他山之石】白话生成对抗网络GAN及代码实现

白话生成对抗网络 GAN，50 行代码玩转 GAN 模型！【附源码】

神经网络中Epoch、Iteration、Batchsize相关理解和说明_unique-R的博客-CSDN博客_epoch神经网络

未完待续......