图像处理数学基础
泛函分析
- 函数:数域->数域
- 泛函:函数->数域
- 算子:函数->函数
在适当的函数类中选择一个函数使得某值取得最值,变分法就是求泛函极值的方法。
泛函分析在图像处理应用:
- 图像去噪
- 图像分割
以分割曲线为参数构造能量泛函,使曲线与目标重合的时候能量最小,不重合的时候始终大于零。通过最小化能量方程,就可以求出目标的轮廓。即将图像分割过程转变为求解泛函的最小值的过程。 - 机器学习模型选择
变换分析
正交变换:为了用正交函数或正交矩阵表示图像而对原图像所做的线性可逆变换。
正交变换有能量集中和去除相关性的性质。
在变换域中,图像能量集中分布在低频率成分上。边缘、线状信息反映在高频率成分上,有利于图像处理。
正交变换广泛用于图像特征提取、图像编码、图像增强、图像复原、图像识别等。
图像工程中的主要正交变换
- 傅里叶变换
- 离散余弦变换
- 霍特林(K-L)变换
- 沃尔什变换
- 小波变换
傅里叶级数
任何周期函数都可以表示为不同频率的正弦和的形式,每个正弦和乘以不同的系数。
傅里叶变换
非周期的函数(曲线有限)可以用正弦和乘以加权函数的积分来表示。
用傅里叶级数或变换表示的函数特征可以完全通过傅里叶反变换来重建,且不丢失任何信息。
连续函数的傅里叶变换是波形分析的有力工具。
离散傅里叶变换使数学方法与计算机级数建立了联系。
傅里叶变换提供从另一个角度来观察图像,可以将图像从灰度分布转化到频率分布上来观察图像的特征。
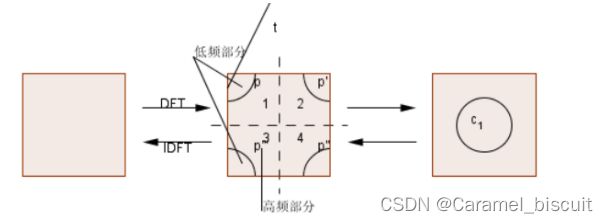
图像的频率是表征图像中灰度变化剧烈程度的指标,图像的边缘是突变部分,变化较快,因此是高频分量。
图像的噪声大部分情况下是高频部分,图像平缓部分则为低频分量。
图像的DCT变换
离散余弦变换具有很强的“能量集中”特性。大多数的自然信号的能量都集中离散余弦变换后的低频部分。
DCT应用
在静止图像编码标准JPEG、运动图像编码标准MJPEG和MPEG的各个标准中都使用了离散余弦变换。
实现特征提取的途径-降维
1.简化计算,便于分析
2.去掉冗余,显现特征
K-L变换是一种基于目标统计特性的最佳正交变换。
特点:K-L变换能够充分去除相关性,把有用的信息集中到数目尽量可能少的主分量中。
应用:主要用于图像压缩、图像旋转、图像增强、遥感多光谱图像的特征提取与信息融合。
霍特林(K-L)变换
在实际应用中,将图像看成随机矢量,具有N个像素的图像f(i,j)在某个通信信道传输了M次,接收到的是一个图像样本集合{f1(i,j),…,fM(i,j)},若用xk表示获得的图像fk(m,n),图像样本集合可表示为{x1,x2,…xM}.
基于PCA的训练数据增强
Alex网络
动机:目标是不随着光照强度和颜色而改变的。
做饭:使用PCA对于训练数据进行增强:对于每一个RGB图像进行一个PCA的变换,对主成分做一个标准差为0.1的高斯扰动,每一轮重新生成一个尺度因子。
PCA VS LDA
- PCA是无监督的,LDA是有监督的。
- PCA是去掉原始数据冗余的维度,LDA是选择一个最佳的投影方向,使得投影后相同类别的数据分布紧凑,不同类别的数据尽量相互远离。
傅里叶变换(FT)缺陷
FT变换适于分析平稳信号。
实际中大多数信号含有大量的非平稳成分,如:突变、奇异、起点,终点等,它们的频域特性都随时间而变化,对此FT并不适合。
原因:FT丢掉了时间信息,无法根据变换的结果判断一个特定的频率是在什么时候发生的。
短时傅里叶(STFT)
基本信号:给信号加一个小窗,主要集中在对小窗内的信号进行变换,反映了信号的局部特征。
把信号划分成许多小的时间间隔,用傅里叶变换分析每一个时间间隔,以便确定该时间间隔存在的频率。
STFT的处理方法是对信号施加一个滑动窗(反映滑动窗的位置)后,再做傅里叶变换。
STFT缺陷
1.其窗函数的大小和形状均与时间和频率无关,保持固定不变,对于分析时变信号不利。(高频信号持续时间短,所以希望对于高频采用小的时间窗,低频使用大时间窗进行)。
2.不能构成正交基,给数值计算带来不便。
小波变换
小波函数必须满足两个条件:
1.小:小波的振幅只能在一个很短的一段区间上非零,具有衰减性,是局部化的。
2.波:小波具有波动性,是振荡的。
小波是一个具有振荡性和迅速衰减的波。
基小波经过平移和伸缩得到一组小波基
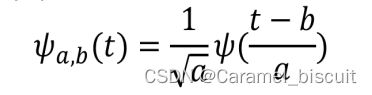
a:尺度因子,b:平移因子
(1)缩放(尺度变换):压缩或伸展基本小波,尺度系数越小,则小波越窄。

小波尺度和信号频率的关系:
尺度a较大时,距离远视野宽,分析频率低,概貌观察。
尺度a较小时,距离近视野窄,分析频率高,细节观察。
(2)平移:小波的延迟或超前。
离散小波变换(DWT)
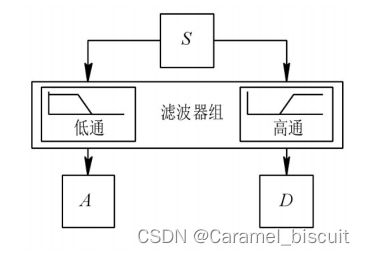
执行离散小波变换的有效方法是使用滤波器。
双通道子带编码。
一个为低通滤波器,得到信号的近似值A。
一个为高通滤波器,得到信号的细节值D。
高斯信号的特性:
- 高斯信号与一固定数值相加的结果,只改变噪声平均值,其它特性不变。
- 高斯信号的线性组合仍是高斯信号。
- 高斯信号通过线性系统后,仍是高斯信号。
高斯混合模型(Gaussian Mixed Model,GMM)
多个高斯分布函数的线性组合,理论上GMM可以拟合出任意类型的分布,可用于解决同一集合下的数据包含多个不同的分布的情况。
背景建模-视频目标检测
背景变化特定:在摄像机固定的情况下,背景的变化时缓慢的,而且大都是光照,风等影响。如水面波纹、摇摆树枝、飘扬的旗帜,通过对微小重复运动的背景建模。从而分离出前景和背景。
高斯混合建模::考虑到背景的多模态,将图像中每一个像素点的值看成是一个服从高斯分布的随机变量。一般的混合高斯模型采用3-5个单高斯模型进行混合。
- 参数初始化
在第一帧图像时,每个像素对应的第一个高斯分布进行初始化,均值赋为当前像素的值,权值赋为1。除第一以外的高斯分布函数的均值、权值和初始化零。 - 判定
在时刻t对图像帧中的每个像素与它对应的高斯模型进行匹配,匹配是背景,不匹配是前景。 - 参数更新