三维点云处理系列----PCA

一、主成分分析

PCA推导的基础数学知识准备
1、矩阵和向量相乘
矩阵和向量相乘实际是矩阵对向量进行旋转加拉伸作用。可以试试例子：矩阵为[(0,1),(2,1)],向量为（1,0）’,相乘之后向量变成了（0,2）’。进行了旋转和拉伸。但是，如果向量刚好是矩阵的特征向量的时候，矩阵只会对向量有缩放的效果，不会有旋转。
2、SVD分解
一个矩阵，可以分解成三个矩阵相乘的形式。

U和V都是酉矩阵，即

Σ是一个对角阵。所以也可以从SVD的角度来理解矩阵和向量乘法的一个物理意义。U,V值会对向量进行旋转变换，而Σ会对向量进行缩放变换。
3、瑞利商
瑞利商的简要理解：向量被一个矩阵相乘之后，相当于是进行了拉伸和旋转变换，拉伸变换的倍数是不超过矩阵A的特征值的最大最小值的。
瑞利商被用来求解PCA当中投影方差的最大最小值，从而得出投影主向量。

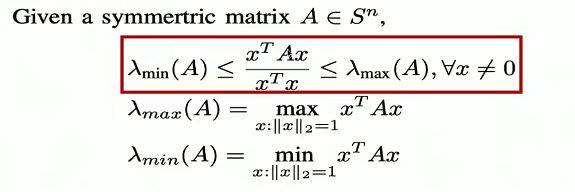
PCA的过程：
PCA的主要思想是：对输入的数据进行换基底的操作，使得数据在PCA得到的基底上有更好的表示。比如最大主向量，就是使得数据在最大主向量上分布更加分散，投影的方差最大。
对数据求均值，进行去中心化，得到去中心化之后的矩阵X
假设投影主向量为z,投影的长度大小为X’z,则投影的均值为X’z各个元素加和求均值
投影的方差：因为X先经过了去中心化，在合并化简的时候就等于均值矩阵X在z方向上投影的平方，最后使用瑞利商求方差最大化，发现方差最大的时候，对应的投影方向就是均值矩阵XX’的最大特征值对应的特征向量。

4、核PCA
PCA针对线性数据可以较好的提取出主向量对数据进行表示，但是对于非线性数据就不能较好的表示。
核PCA主要思想是：把当前的数据升高一个维度，在较高的维度里去表示当前的数据就能清晰的表示出来。核心关键是找出一个变换使得低维空间数据点转换到高维空间。

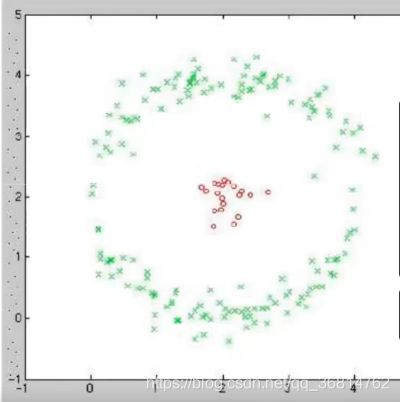
上升到高维空间后

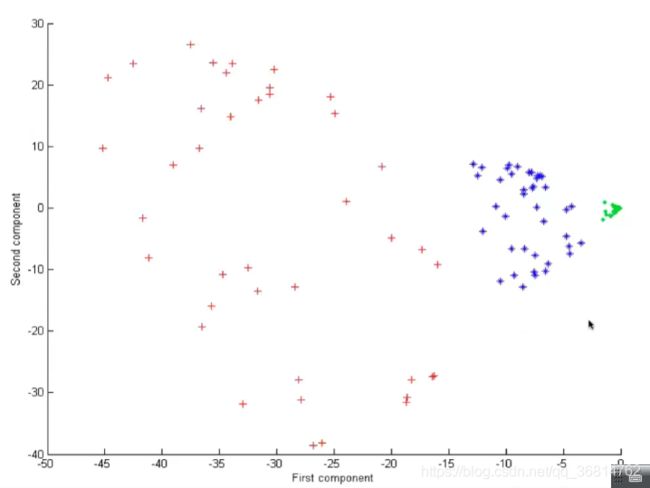
5、PCA应用
法向量计算
基本步骤：
１．随机选取出一个点
２．以改点为中心点，选取邻域中ｋ个点出来
３．以这ｋ个点作为一组数据输入到pca求出数据的主向量
４．选取出特征值最小的特征向量即为法向量方向

6、点云滤波算法
点云滤波voxel filter

出发点问题
对于体素中的点，保留那一个点作为输出比较好？
思路有两种：选取一个ｖｏｘｅｌ中的平均坐标点作为滤波输出；或者进行随机选取一个点作为输出

voxel filter的一般流程：

１．计算点云的整体空间范围，得出点云空间的最大、最小范围
２．设定体素大小r，计算出空间划分的份数索引
Ｄ_x=(x_max-x_min)/r
Ｄ_y=(y_max-y_min)/r
Ｄ_z=(z_max-z_min)/r
３．计算每个点的分组索引
hx = floor((x-x_min)/r)
hy = floor((y-y_min)/r)
hz = floor((y-y_min)/r)
index = hx+hy*D_x+hz*Dx*Dy
４．对每个点的索引进行排序，处在同一个体素的索引相同，相同索引聚集到一起
５．对每个体素中的点进行降采样

另外一种不采用排序的方法：使用哈希表映射，把所有点都映射到哈希表中，对于处于同一个位置的点进行采样输出。
hash(hx,hy,hz) = index % hash_size
但有可能处于不同体素的点会被映射到同一个哈希容器中，这时候就是存在冲突，需要对其进行冲突检测,比如哈希容器大小为１００，索引为１９１，２９１的两个点不属于同一个体素，但是经过映射都被映射到了９１这个容器。

课后作业代码编写：

# 实现PCA分析和法向量计算，并加载数据集中的文件进行验证
import open3d as o3d 
import os
import numpy as np
from pyntcloud import PyntCloud

# 功能：计算PCA的函数
# 输入：
#     data：点云，NX3的矩阵
#     correlation：区分np的cov和corrcoef，不输入时默认为False
#     sort: 特征值排序，排序是为了其他功能方便使用，不输入时默认为True
# 输出：
#     eigenvalues：特征值
#     eigenvectors：特征向量
def PCA(data, correlation=False, sort=True):
    #1计算数据均值
    data_mean = np.mean(data, axis=0)
    #2对数据进行去中心化
    data = data - data_mean
    #3对去中心化的数据H = Ｘ'X矩阵奇异值分解，求特征值和特征向量
    ##注意ｄａｔａ中存储的格式是ＮX3,协方差矩阵描述的是各个维度之间的相关性，所以协方差矩阵大小为３ｘ3.并且协方差矩阵为对称矩阵
    ##对角线上为各个维度内的方差，非对角线上为各个维度间的方差
    #对称矩阵分解出来的Ｕ和Ｖ是互为转置矩阵
    H = np.dot(data.T, data)
    #H = np.cov(data, rowvar=False)
    eigenvectors, eigenvalues, eigenvectors_t = np.linalg.svd(H)
    #4对特征值和特征向量进行排序
    if sort:
        sort = eigenvalues.argsort()[::-1]
        eigenvalues = eigenvalues[sort]
        #U中的列向量为特征向量
        eigenvectors = eigenvectors[:, sort]

    return eigenvalues, eigenvectors


def main():
    # 加载原始点云
    point_cloud_pynt = PyntCloud.from_file("airplane_0529.ply")
    point_cloud_o3d = point_cloud_pynt.to_instance("open3d", mesh=False)
    o3d.visualization.draw_geometries([point_cloud_o3d]) # 显示原始点云
    # 从点云中获取点，只对点进行处理
    points = point_cloud_pynt.points
    print('total points number is:', points.shape[0])
    size = points.shape[0]
    # 用PCA分析点云主方向
    w, u = PCA(points)
    point_cloud_vector = u[:, 0] #点云主方向对应的向量
    print('the main orientation of this pointcloud is: ', point_cloud_vector ,'and',w[0])
    print('the second orientation of this pointcloud is:',u[:, 1])
    print('the second orientation of this pointcloud is:',u[:, 2])

    # 循环计算每个点的法向量
    pcd_tree = o3d.geometry.KDTreeFlann(point_cloud_o3d)
    normals = []

    # 1.选取一个点,搜索１０个邻近点
    for i in range(size):
      [_, idx, _] = pcd_tree.search_knn_vector_3d(point_cloud_o3d.points[i], 10)
      k_nearest_point = np.asarray(point_cloud_o3d.points)[idx, :]  #按照ｉｄｘ取出k个近邻点
    # 2.选取改点的一个邻域，计算该邻域内的点的PCA
      u_1, v_1 = PCA(k_nearest_point)
      
    # 3.选取出特征值最小对应的特征向量作为法向量方向
      normals.append(v_1[:,2])

    normals = np.array(normals, dtype=np.float64)

if __name__ == '__main__':
    main()

python处理点云相关库、函数记录熟悉

numpy库

numpy.mean(a, axis, dtype, out，keepdims )   

经常操作的参数为axis，以m * n矩阵举例：
axis 不设置值，对 mn 个数求均值，返回一个实数
axis = 0：压缩行，对各列求均值，返回 1 n 矩阵
axis =1 ：压缩列，对各行求均值，返回 m *1 矩阵

H = np.dot(data.T, data)

点乘运算

eigenvectors, eigenvalues, eigenvectors_t = np.linalg.svd(H)

奇异值分解：
函数：np.linalg.svd(a,full_matrices=1,compute_uv=1)。

参数：
a是一个形如(M,N)矩阵
full_matrices的取值是为0或者1，默认值为1，这时u的大小为(M,M)，v的大小为(N,N) 。否则u的大小为(M,K)，v的大小为(K,N) ，K=min(M,N)。
compute_uv的取值是为0或者1，默认值为1，表示计算u,s,v。为0的时候只计算s。
返回值：
总共有三个返回值u,s,v
u大小为(M,M)，s大小为(M,N)，v大小为(N,N)。
A = usv

排序：

sort = eigenvalues.argsort()[::-1]#返回eigenvalues中元素从大到小的索引

x.argsort()
#输出x中元素从小到大排列的对应的index(索引)

[::-1]两个冒号，三个数，起始：结尾（不包括）：间隔。
最后为-1代表逆序。

H = np.cov(data, rowvar=False)
def cov(m, y=None, rowvar=True, bias=False, ddof=None, fweights=None,aweights=None)

m:一维或则二维的数组，默认情况下每一行代表一个变量（属性），每一列代表一个观测
y:与m具有一样的形式的一组数据
rowvar:默认为True,此时每一行代表一个变量（属性），每一列代表一个观测（一个点）；为False时，则反之

协方差矩阵求解

矩阵拼接：

data_index_point = np.c_[index, point_x, point_y, point_z]
np.r_是按列连接两个矩阵，就是把两矩阵上下相加，要求列数相等。
np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。

python点云数据处理

#读取加载点云
PyntCloud.from_file("airplane_0529.ply")