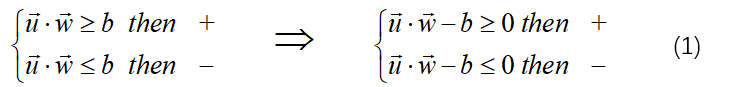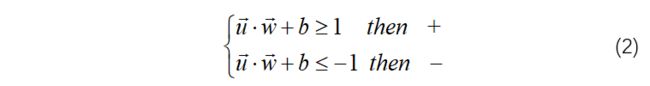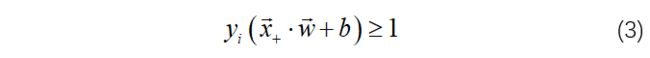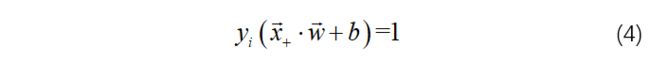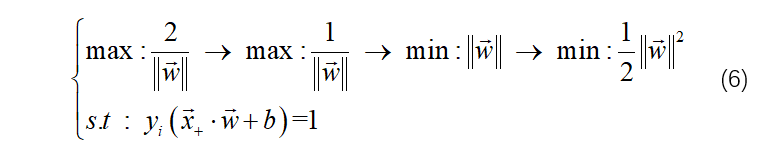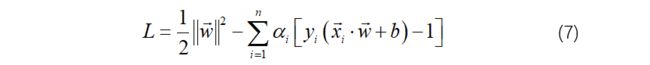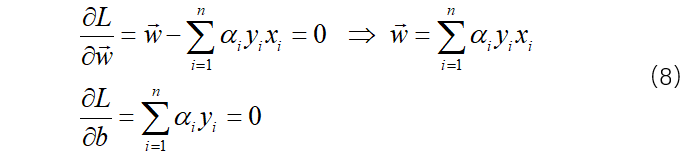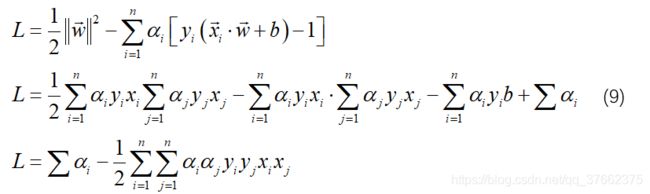机器学习系列（1）SVM的公式推导

机器学习与深度学习

        在深度学习“家喻户晓”之前，这种技术一直以“神经网络”的名义活跃于学者们的研究和工作者们的项目中。深度学习或者神经网络都属于机器学习的一个子类，理所当然地深度学习会具备机器学习中的一些共有特性，尽管近几年深度学习发展出了很多“专属”问题。近期更新的这个系列我们会以机器学习中常见算法的一些特殊性出发，探究一下它们会对我们的日后深度学习的学习带来哪些启发。

一 SVM的推导过程与其本身同样重要

        支持向量机（SVM）是一类监督学习式的机器学习算法，其决策边界是对学习样本求解的最大边距超平面。SVM算法在中小规模的数据集中的表现非常令人满意，对我们的深度学习来说更有意义的部分是它的推导过程，深度学习的优势在于对原始特征的重构，而SVM在已经有一些很好的表示特征情况下，它的性能同时可以得到很好的理论保证，而在一些场景中模型能否得到有效的理论保证是决策者判断是否选用该模型的关键，如辅助医疗、自动驾驶领域等。通过SVM的推导我们来了解这种机器学习算法，并将其与之后的深度学习进行对比，也许会给你带来一些启发。

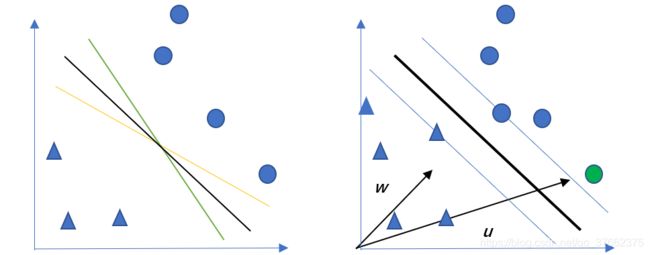
        考虑这样一个问题，一个决策边界将样本划分为正样本(○)和负样本(△)，而此决策边界可以有很多种表达方式，如图1.1中三种决策边界都可以实现我们想要的效果。那么，我们依据什么来判断哪种决策边界是最好的？

                          左图为1.1 几种边界示意图                                                    右图为1.2 SVM假设示意图

        在此我们做出一个假设如图1.2所示：定义与决策边界（粗）相互平行、距离相等的两条直线边界（细），该直线边界经过距离决策边界最近：两个样本，那么令两条直线边界间隔最大的决策边界的位置即是我们所求。接下来我们使用数学语言描述。

        存在垂直于决策边界的向量w和向量为u的任意一个待检测样本（xi,yi），则决策过程可以描述为：u在w方向的投影大于某个值b即判定为此样本为正样本，相反地如果小于值b则判定为负样本。（向量投影也就是距离在求解时集的还要除以一个被投影向量的模，这里是经过b调节使得形式更加简单些）

        目前为止，我们可以理解为一个SVM的问题的本质就是通过样本的学习向量w，对一个新的样本进行预测就是将其带入上式后与0进行对比，即可得到样本的归类结果。考虑经过样本边界，则在训练集中应该满足公式(2)，这也被称为最大间隔假设。

        需要注意的是，这里的1和-1可以是以0位分界线的任意两个数字，可以通过w和b的调整进行伸缩变化，选择1与-1是为了数学运算的方便，同时标签值设置的就是1与-1。（这里这样理解：等于0不就在中间的边界上了吗，所以自然是要分类讨论两种情况，也就是最大化间隔区域的两个边界，所以当然要与间隔的边界进行比较，然后通过缩放统一到1与-1）

        如将最大边界假设合写，当yi =+1或-1，则：

        显然地，位于样本边界上的点需满足：

       那么间隔的大小可以表示为：

       这里可能需要解释一下：这里是个分类讨论，x为正样本y是+1，x是负样本y是-1，负的x的负样本等于正样本，两者才能抵消

       关于间隔大小周志华老师西瓜书中的那种也很容易理解：点到一条直线的距离。     

这里就是一个向量的减法，位于间隔边界上的一个正样本的向量与一个负样本向量的差值向量在w向量方向上的投影的大小就是间隔大小。最终的这个式子很简单，只关于w。我们的任务是最大化间隔，则我们的任务可以转化为这样一个过程：

 

二 拉格朗日lagrange乘子法求解

       观察（6）式，是一个有约束的求极值点的问题，也就是条件极值，常用方法为拉格朗日乘子法。

       拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法，表示为：

       公式（7）分别求偏导：

       将（8）中结果带入（7）式中：

         公式（9）所揭露的意义为：我们的目的是使得模值最小，我们可以记录下使得α不为0（时的（xi，yi），以及相应的拉格朗日lagrange乘子法公式中的参数α，即可令模最小。我们还得出结论：L只取决于样本之间的两两点乘，这非常有利于我们的求解。最后判别条件可整理为更简单的模式：

                                                         

        一个新的样本u只要与这些样本训练后与不为0的α以及对应的（xi，yi）相乘大于等于0即可判断为正样本，同理小于等于0为负样本。

        有一句话用来描述拉格朗日算法很容易理解：拉格朗日算法可以将k个变量在L个约束下的最小化问题转变为K+L个变量的无约束优化问题（存在几个约束条件就需要引入几个额外变量）。  无约束优化问题我们更常见，一般使用迭代法求解，这里常用一种SMO方法，通俗点说就是固定一个或几个变量迭代其他变量。后来我发现SMO是专门针对SVM提出的优化算法，SVM真的是有一整套自己的非常优美的推导过程，怪不得DL出现之前如此受欢迎。

        这里还有需要注意的一点是：这里只考虑了等式约束，其实实际应用中还有很多不等式约束，这里为了避免混淆先不讲述了，想要了解请看这里：https://www.bilibili.com/video/BV17J411C7zZ?p=82

 

三 SVM的核方法

        为什么要使用核方法：从模型角度来说上述的讨论都是针对线性的间隔，我们需要从一个更高维的角度来求借一个SVM问题，这就需要进行一个高维的映射。然后再从优化角度来说我们要计算一个对偶产生的内积，这就需要使用一个“核”来简化运算

1非线性带来高维转换

        这里很重要的一点是上面的结论都是针对线性可分情况的讨论，但我们解决的问题大多数都是非线性的。有三个例子（严格的cover定理、分蛋糕问题、解决异或问题）可以证明一个现象：当前维度线性不可分的问题，在更高的维度线性可分。于是我们将xi*xj进行一个特征空间的映射以提升维度xi*xj --> φ（xi）*φ（xj）

2对偶产生内积

        φ（xi）* φ（xj）是一个比较不易求解的部分，但我们并不关心φ（xi）或者φ（xj）单独的个体，我们关心的是两者的内积。如果通过一个可代替的函数（也就是我们说的核SVM中的核）来代替这个内积的结果，将使得计算变得非常容易，事实上经证明这样的函数是存在的，也就是核函数

 

四 软边界     

        软边界代表SVM允许一点点的错误，不严格寻找“支持向量”。6.28是最大间隔

  

       使用的“损失函数”有没有感觉像是一种DL中的“激活函数”，所以说SVM是很强的且有很大的潜力。

       包括scikit-learn在内的很多第三方模块都对常用的机器学习方法进行了封装，他们很容易被调用。且机器学习SVM算法的程序实现不作为本书的介绍内容，故不在此介绍SVM的程序实现。我们在本章推导了机器学习中的算法之一SVM，这有利于我们理解这种流行于深度学习技术之前的经典算法的优势所在，它可以作为我们在今后的深度学习技术探索过程中的基础参考模型。