一文读懂Embedding
文章目录
-
- 一、**什么是Embedding?**
- 二、One-Hot编码
- 三、**怎么理解Embedding**
- **四、Word Embedding**
一、什么是Embedding?
“Embedding”直译是嵌入式、嵌入层。
简单来说,我们常见的地图就是对于现实地理的Embedding,现实的地理地形的信息其实远远超过三维,但是地图通过颜色和等高线等来最大化表现现实的地理信息。
通过它,我们在现实世界里的文字、图片、语言、视频就能转化为计算机能识别、能使用的语言,且转化的过程中信息不丢失。
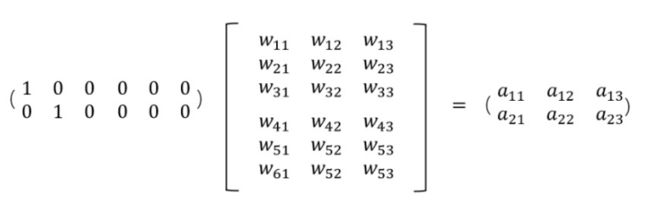
Embedding层,在某种程度上,就是用来降维的,降维的原理就是矩阵乘法。
二、One-Hot编码
One-Hot 编码是分类变量作为二进制向量的表示。
- 将分类值映射到整数值。
- 然后,每个整数值被表示为二进制向量,除了整数的索引之外,它都是零值,它被标记为1。
举例:
运动特征:[“足球”,“篮球”,“羽毛球”,“乒乓球”](N=4):
足球 => [1,0,0,0]
篮球 => [0,1,0,0]
羽毛球 => [0,0,1,0]
乒乓球 => [0,0,0,1]
优点:
- 解决了 分类器不好处理离散数据 的问题。将离散型特征使用 one-hot 编码,会让特征之间的距离计算更加合理。
- 在一定程度上也起到了 扩充特征 的作用。
缺点:
在文本特征表示上有些缺点就非常突出了。
- 它是一个词袋模型,不考虑词与词之间的顺序(文本中词的顺序信息也是很重要的);
- 它假设词与词相互独立(在大多数情况下,词与词是相互影响的);
- 它得到的特征是离散稀疏的 (这个问题最严重,Embedding降维就是对此优化)。
三、怎么理解Embedding
由于One-Hot编码过于稀疏,过度占用资源,我们使用Embedding对其降维。
假设:我们有一个2 x 6的矩阵,然后乘上一个6 x 3的矩阵后,变成了一个2 x 3的矩阵。
Embedding层,在某种程度上,就是用来降维的,降维的原理就是矩阵乘法。
可以降维,那么embedding也可以升维,对低维的数据进行升维时,可能把一些其他特征给放大了,或者把笼统的特征给分开了。
四、Word Embedding
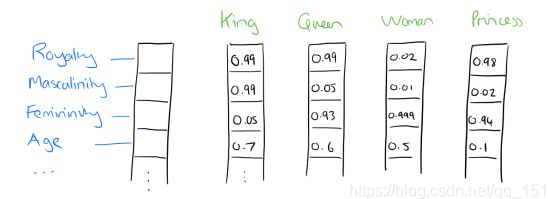
比如将词汇表里的词用 “Royalty”, “Masculinity”, “Femininity” 和 “Age” 4个维度来表示,King 这个词对应的词向量可能是 (0.99,0.99,0.05,0.7)。
在实际情况中,有时并不能对词向量的每个维度做一个很好的解释,但我们知道他是某一个维度的特征就可以了。
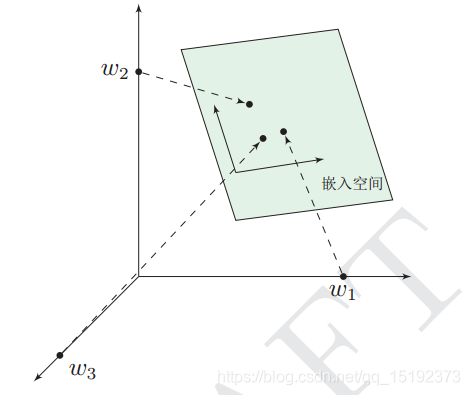
这个过程称为 word embedding(词嵌入),即将高维词向量嵌入到一个低维空间。如图:
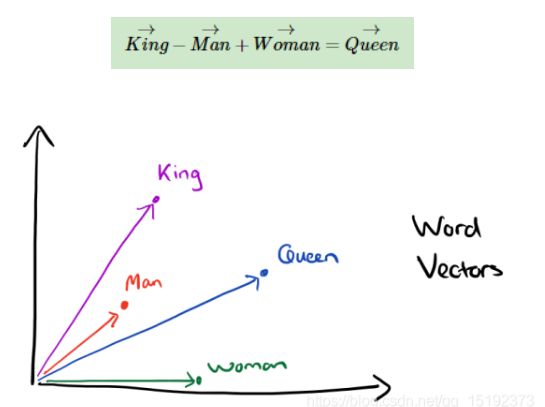
经过我们一系列的降维神操作,有了用 representation 表示的较短的词向量,我们就可以较容易的分析词之间的关系了,比如我们将词的维度降维到 2维,有一个有趣的研究表明,用下图的词向量表示我们的词时,我们可以发现:
queen(皇后)= king(国王)- man(男人)+ woman(女人)
这样计算机能明白,“皇后啊,就是女性的国王”
walked(过去式)= walking(进行时)- swimming(进行时)+ swam(过去式)
同理计算机也能明白,“walked,就是walking的过去式”
另外,向量间的距离也可能会建立联系,比方说“北京”是“中国”的首都,“巴黎”是“法国”的首都,那么向量:|中国|-|北京|=|法国|-|巴黎|
式”
另外,向量间的距离也可能会建立联系,比方说“北京”是“中国”的首都,“巴黎”是“法国”的首都,那么向量:|中国|-|北京|=|法国|-|巴黎|