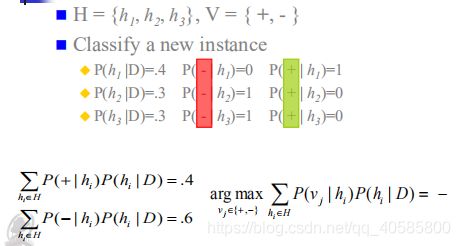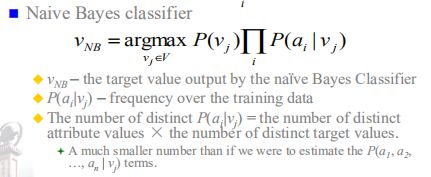贝叶斯学习的简单介绍
文章目录
-
-
-
- 贝叶斯学习 Bayesian Learning
- 一、介绍
-
- 1.1 先验概率
- 1.2 后验概率
- 二、贝叶斯理论
-
- 2.1 举例介绍
- 2.2 MAP假设
- 2.3 概率法则
- 三、最小描述长度假设
- 四、贝叶斯最优分类器
- 五、Gibbs算法
- 六、Bagging分类器
- 七、朴素贝叶斯分类器
- 八、贝叶斯信念网络
- 九、总结
-
-
贝叶斯学习 Bayesian Learning
一、介绍
贝叶斯概率论于1764年提出。
贝叶斯学习提供了定量的方法来衡量证据如何支持其他假设。
贝叶斯决策理论是一种基本的统计方法,它利用决策所伴随的概率和成本来量化各种决策之间的权衡。
首先,我们假设所有的概率知道。那么,我们将研究概率结构不完全已知的情况。
1.1 先验概率
先验概率是指根据以往经验和分析得到的概率,它往往作为"由因求果"问题中的"因"出现。
那么,如何通过先验概率做决策呢?
- 如果 P(w1) > P(w2),则决策结果——w1
- 如果 P(w1) ≤ P(w2),则决策结果——w2
这种决策的误差是:P(error) = min{P(w1), P(w2 )}
1.2 后验概率
后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,是"执果寻因"问题中的"因"。
贝叶斯学习方法的特点:
- 每一个观察到的训练例子都可以增加或减少假设正确的估计概率(灵活性)
- 先验知识可以与观测数据相结合来确定一个假设的最终概率
- 贝叶斯方法可以适应进行概率预测的假设
- 通过组合新的假设,可以对多个假设进行加权分类
- 可以为评估假设提供一个黄金标准
二、贝叶斯理论
2.1 举例介绍
贝叶斯决策理论早于决策树学习和神经网络,应用在统计学理论领域。
目标:学习到最好的假设。贝叶斯学习中:“最好的假设“就是“最可能的假设”。
Bayes定理允许基于如下因素来计算可能的假设:
- 假设先验概率
- 假设条件下观察某些数据的概率
- 观测数据本身
给定数据D加上H中各种假设的先验概率的任何初始知识,我们得到以下符号:
- h的先验概率P(h):它反映了我们在观察数据之前所掌握的关于h∈h是一个正确假设的任何背景知识
- D的先验概率,P(D):它反映了在不知道哪个假设成立的情况下,训练数据D被观察到的概率。
- 条件概率,P(D | h):它表示在假设h∈h成立的某个世界中观测数据D的概率。
- 后验概率,P(h | D):它表示给定观测训练数据D时h保持不变的概率。这是机器学习研究人员感兴趣的数量。
于是可以通过此公式计算后验概率,这也是贝叶斯学习方法的基石:
P(h | D)= P(D | h) P(h)/ P(D)*
2.2 MAP假设
在许多学习场景中,目标是在给定观测数据D的情况下,从一组候选假设h中找到最可能的假设h,任何这种最大似然假设都被称为最大后验概率假设。(Maximum A Posteriori (MAP) 假设)
贝叶斯理论可用于确定MAP假设:
h = argmax(h∈H) P(h | D)
= argmax(h∈H) P(D | h)* P(h)/ P(D)
= argmax(h∈H) P(D | h)* P(h)
如果每个假设h在假设集H中的概率是相等的,则我们只需要计算使得P(D | h)最大的h即可,MAP会演化为极大似然**Maximum Likelihood **(ML)。即h = argmax(h∈H) P(D | h)
2.3 概率法则
- P(A ∩ B) = P(A|B)P(B) = P(B|A)P(A)
- P(A∪B) = P(A) + P(B) - P(AB)
- 如果A、B事件相互独立:则 P(A ∩ B) = P(A)P(B) ,且P(ABC…) = P(A)P(B)P©…
- 奥卡姆的剃刀:最简单假设→描述长度最短的假设
三、最小描述长度假设
Minimum Description Length Principle(MDL)
hMDL = argmin(h∈H) Lc1(h)+ Lc2(D | h)
其中:
Lc1(h)是假设表述的比特长度(——表示模型复杂度)
Lc2(D | h)是使用假设h进行编码时,数据D描述的比特长度(——表示错误)
Lc(x)是在方案c下编码x的最小比特长度
最小描述长度假设和最大后验概率假设本质上是相同的
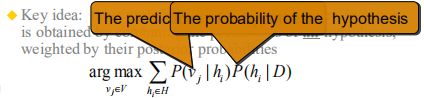
四、贝叶斯最优分类器
Bayes optimal classification,同时考虑所有的假设并且进行加权。
argmax(vj∈V) Σ(hi∈H) P(vj|hj)P(hi|D)
该方法使新实例正确分类的概率最大化。
使用相同的假设空间和相同的先验知识的分类方法没有一种方法能比这种方法的平均性能好。
这种方法所做的预测与H中没有包含的假设相对应。
存在的问题:需要对所有可能的模型/假设进行总结,当模型的假设空间很大时,它是昂贵的或不可能的。
解决方案:抽样——Gibbs算法
五、Gibbs算法
Gibbs算法:根据h上的后验概率分布P(h | D),从h中随机选择一个假设h,使用h对新实例x进行分类。
在一定条件下,该算法期望误差最多为Bayes最优分类器的两倍(Harssler等人。1994年)。
可以通过从P(h | D)中抽样多个假设并平均其分类结果来改进。
- 马尔可夫链蒙特卡罗(MCMC)抽样
- 重要性抽样
缺点:从P(h | D)中抽样是很困难的。
由此提出了Bagging分类器——通过对训练样本的抽样实现抽样P(h | D)
六、Bagging分类器
Bagging分类器——通过对训练样本的抽样实现抽样P(h | D)
Boostrap 采样,(使用bootstrap采样和从P(h | D)中采样几乎是相同的):
- 通过随机抽取m个示例创建Di,替换D
- Di期望从D中漏掉37%的实例
Bagging 算法:
- 创建k个bootstrap样本D1,D2,…,Dk
- 在每个Di上训练不同的分类器hi
- 利用等权分类器投票对新实例进行分类
例如:经过实证研究,使用Bagging的决策树比单纯的决策树要效果好。
模型的Error通常同时要考虑偏差和方差,即:Error = Bias + Variance
其中Bias,偏差,指的是模型预测值和真实值的差别;Variance,方差,指的是模型对给定数据集进行预测的变化率。
Bagging分类器比单一分类器表现的好的原因就在于它可以有效降低模型的方差。
七、朴素贝叶斯分类器
假设属性取值ai之间互相独立。
Vnb:朴素贝叶斯分类器的输出结果
P(ai|vj):满足vj的条件下各个属性值(相互独立)的频率
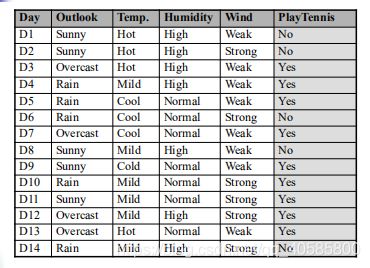
一道题目:
因此 Vnb = no,且目标值为no的条件概率为:0.0206/0.0206+0.0053 = 0.795
八、贝叶斯信念网络
贝叶斯最有分类器应用成本较高;朴素贝叶斯使用条件独立假设,在许多场景下这样的假设是有局限性的。
贝叶斯信念网络提供了一种折衷的方案——允许声明适用于变量子集的条件独立性假设。
贝叶斯信念网络是一种概率图形模型,它表示:
- 通过有向无环图(DAG)得到的一组变量及其条件独立性
- 变量集合的联合概率分布
例如,贝叶斯网络可以表示疾病和症状之间的概率关系。给定症状,网络可用于计算各种疾病出现的概率。
形式上,贝叶斯网络是有向无环图:
- 节点表示贝叶斯意义上的变量:可以是可观测量、潜在变量、未知参数或假设。
- 边表示条件依赖
- 未连接的节点表示相互有条件独立的变量。
- 每个节点与一个概率函数相关联,该函数将节点父变量的一组特定值作为输入,并给出节点所代表变量的概率。
- 例如,如果父项是m个布尔变量,那么概率函数可以用一个包含2m个条目的表来表示,其父项的2m个可能组合中的每个条目都有一个条目为真或假。
九、总结
- 贝叶斯方法为概率学习方法提供了基础,该方法适应(并要求)关于替代假设的先验概率和观察给定假设的各种数据的概率的知识。
- 贝叶斯方法允许根据这些假设的先验和观测数据为每个候选假设分配一个后验概率。
- 贝叶斯方法可以用来确定给定数据的最可能假设——最大后验概率(MAP)假设。(这是最佳假设,因为没有其他假设更有可能)
- Bayes最优分类器结合了所有备选假设的预测,并按其后验概率加权,以计算每个新实例的最可能分类
- naive bayes分类器是一种贝叶斯学习方法,在许多实际应用中得到了广泛的应用。它之所以被称为“天真”,是因为它包含了一个简化的假设,即给定实例的分类,属性值是有条件独立的。当满足这个假设时,天真的Bayes分类器是通常相当有效。
- 贝叶斯信念网络为属性子集之间的条件独立假设集提供了一种更具表现力的表示。
- 最小描述长度原则建议选择最小假设描述长度加上给定假设数据描述长度的最小假设。贝叶斯定理和信息论的基本结果可以为这一原理提供理论依据。