随机梯度下降算法SGD

随机梯度下降算法SGD

参考：为什么说随机最速下降法 (SGD) 是一个很好的方法？

假如我们要优化一个函数$f(x)$ ，即找到它的最小值，常用的方法叫做 Gradient Descent (GD)，也就是最速下降法。说起来很简单, 就是每次沿着当前位置的导数方向走一小步，走啊走啊就能够走到一个好地方了。

如上图, 就像你下山一样，每一步你都挑最陡的路走，如果最后你没摔死的话，一般你很快就能够走到山脚。用数学表示一下，就是

$x_{t+1}=x_t-{\eta }_t\nabla f(x_t)$

这里$x_t$就是第t步的位置，$\nabla f(x_t)$就是导数，${\eta }_t$是步长。所以这个算法非常简单，就是反复做这个一行的迭代。

虽然简单优美，但 GD 算法至少有两个明显的缺陷

**首先，**在使用的时候, 尤其是机器学习的应用中，我们都会面临非常大的数据集。这个时候如果硬要算 $f(x)$ 的精确导数（也别管 $f(x)$是什么了，反正每个机器学习算法里面都有这么个东西），往往意味着我们要花几个小时把整个数据集都扫描一遍，然后还只能走一小步。一般 GD 要几千步几万步才能收敛，所以这样就根本跑不完了。

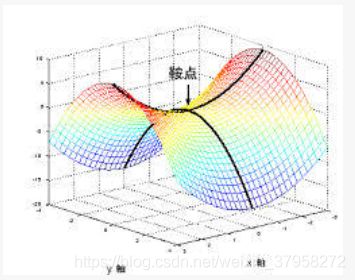
**其次，**如果我们不小心陷入了鞍点，或者比较差的局部最优点，GD 算法就跑不出来了，因为这些点的导数是 0。什么是鞍点:

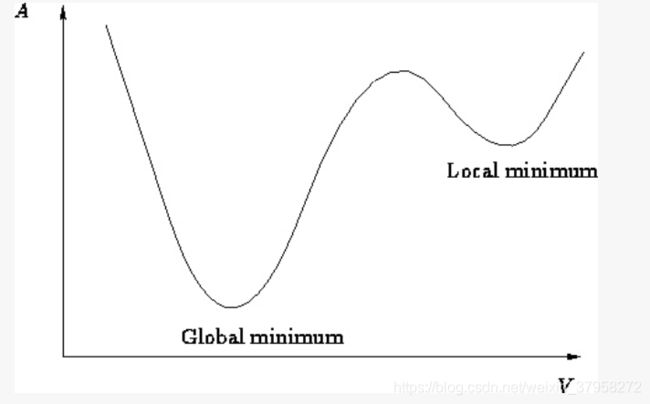
什么是局部最优点（下图右边）：

有趣的是，这两大缺陷竟然可以用同一个方法解决，就是我们今天要谈的 Stochastic Gradient Descent (SGD) 算法。

SGD 算法的表达式和 GD 差不多：

$x_{t+1}=x_t-{\eta }_t\nabla g_t$

这里$g_t$就是所谓的 Stochastic Gradient，它满足$E[g_t]=\nabla f(x_t)$

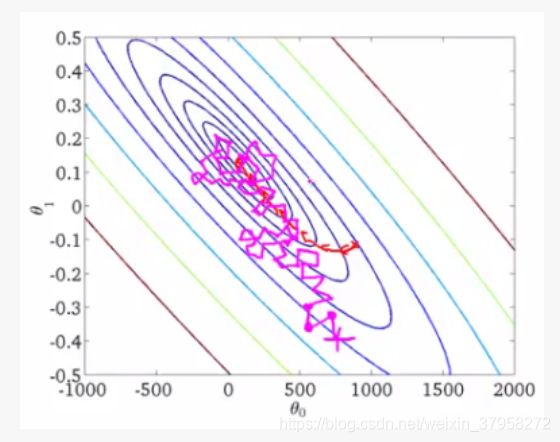
也就是说，虽然包含一定的随机性，但是从期望上来看，它是等于正确的导数的。用一张图来表示，其实 SGD 就像是喝醉了酒的 GD，它依稀认得路，最后也能自己走回家，但是走得歪歪扭扭。（红色的是 GD 的路线，偏粉红的是 SGD 的路线）。

仔细看的话，其实 SGD 需要更多步才能够收敛的，毕竟它喝醉了。可是，由于它对导数的要求非常低，可以包含大量的噪声，只要期望正确就行（有时候期望不对都是可以的），所以导数算起来非常快。就我刚才说的机器学习的例子，比如神经网络吧，训练的时候都是每次只从百万数据点里面拿 128 或者 256 个数据点，算一个不那么准的导数，然后用 SGD 走一步的。想想看，这样每次算的时间就快了 10000 倍，就算是多走几倍的路，算算也是挺值的了。

所以它可以完美解决 GD 的第一个问题——算得慢。这也是当初人们使用 SGD 的主要目的。而且，大家并不用担心导数中包含的噪声会有什么负面影响。有大量的理论工作说明，只要噪声不离谱，其实（至少在 f 是凸函数的情况下），SGD 都能够很好地收敛。

虽然搞理论的人这么说，但是很多完美主义者仍会惴惴不安，觉得用带了随机噪声的导数来训练自己的神经网络不放心，一定要用最准确的导数才行。于是他们往往还会尝试用 GD 跑一遍，和 SGD 得到的结果比较比较。

结果呢？因为我经常干这样的事情，所以我可以负责任地告诉大家，哪怕 GD 训练的时候有多几百倍几千倍的时间，最后结果往往是 SGD 得到的网络表现要比 GD 得到的网络要好得多！

很意外是不是？加了噪声的算法反而更好，这简直就像说＂让马路上的司机多喝点酒，交通能够更顺畅＂一样让人难以接受。

但事实就是如此。实践中，人们发现，除了算得快，SGD 有非常多的优良性质。它能够自动逃离鞍点，自动逃离比较差的局部最优点，而且，最后找到的答案还具有很强的一般性（generalization），即能够在自己之前没有见过但是服从同样分布的数据集上表现非常好！

这是为什么呢？今天我们就简单谈谈为什么它可以逃离鞍点。之后有机会我会再详细介绍 SGD 的别的优良性质——这些性质也是目前优化和机器学习领域研究的热点问题。

那么我们先理解一下，鞍点的数学表达是什么。

首先，我们考虑的情况是导数为０的点。这些点被称为 Stationary points，即稳定点。稳定点的话，可以是（局部）最小值，（局部）最大值，也可以是鞍点。如何判断呢？我们可以计算它的 Hessian 矩阵 H。

• 如果 H 是负定的，说明所有的特征值都是负的。这个时候，你无论往什么方向走，导数都会变负，也就是说函数值会下降。所以，这是（局部）最大值。

• 如果 H 是正定的，说明所有的特征值都是正的。这个时候，你无论往什么方向走，导数都会变正，也就是说函数值会上升。所以，这是（局部）最小值。

• 如果Ｈ既包含正的特征值，又包含负的特征值，那么这个稳定点就是一个鞍点。具体参照之前的图片。也就是说有些方向函数值会上升，有些方向函数值会下降。

• 虽然看起来上面已经包含了所有的情况，但是其实不是的！还有一个非常重要的情况就是 H 可能包含特征值为０的情况。这种情况下面，我们无法判断稳定点到底属于哪一类，往往需要参照更高维的导数才行。想想看，如果特征值是０，就说明有些方向一马平川一望无际，函数值一直不变，那我们当然不知道是怎么回事了：）

我们今天讨论的情况只包含前三种，不包含第四种．第四种被称为退化了的情况，所以我们考虑的情况就叫做非退化情况。

为了说明这一点，首先要引入一个概念：strict saddle 函数。它是说，对于函数定义域内的任意一个点 $x$，满足：

• 函数在 $x$ 点的导数比较大（因而能够做梯度下降）；或者，
• 函数在 $x$ 点附近有最小值（因而已接近完成优化任务）；或者，
• 函数在 $x$ 点的二阶偏导组成的 Hessian 矩阵至少含有一个负的特征值（因而沿着这个方向能够滑下去，降低函数值）。

为什么我们要 x 满足这三个情况的至少一个呢？因为

• 如果 x 的导数大，那么沿着这个导数一定可以大大降低函数值（我们对函数有光滑性假设）
• 如果 x 的 Hessian 矩阵有一个负的特征值，那么我们通过加噪声随机扰动，跑跑就能够跑到这个方向上，沿着这个方向就能够像滑滑梯一样一路滑下去，大大降低函数值
• 如果 x 已经离某一个（局部）最小值很近了，那么我们就完成任务了，毕竟这个世界上没有十全十美的事情，离得近和精确跑到这个点也没什么区别。

所以说，如果我们考虑的函数满足这个 strict saddle 性质，那么 SGD 算法其实是不会被困在鞍点的．那么 strict saddle 性质是不是一个合理的性质呢？

实际上，有大量的机器学习的问题使用的函数都满足这样的性质。比如 Orthogonal tensor decomposition，dictionary learning, matrix completion 等等。而且，其实并不用担心最后得到的点只是一个局部最优，而不是全局最优。因为实际上人们发现大量的机器学习问题，几乎所有的局部最优是几乎一样好的，也就是说，只要找到一个局部最优点，其实就已经找到了全局最优，比如 Orthogonal tensor decomposition 就满足这样的性质，还有小马哥 NIPS16 的 best student paper 证明了 matrix completion 也满足这样的性质。我觉得神经网络从某些角度来看，也是（几乎）满足的，只是不知道怎么证。

下面讨论一下证明，主要讨论一下第二篇。第一篇论文其实就是用数学的语言在说＂在鞍点加扰动，能够顺着负的特征值方向滑下去＂。第二篇非常有意思，我觉得值得介绍一下想法。

首先，算法上有了一些改动．算法不再是SGD，而是跑若干步GD，然后跑一步SGD．当然实际上大家是不会这么用的，但是理论分析么，这么考虑没问题．什么时候跑SGD呢？只有当导数比较小，而且已经很长时间没有跑过SGD的时候，才会跑一次．也就是说，只有确实陷在鞍点上了，才会随机扰动一下下．

因为鞍点有负的特征值，所以只要扰动之后在这个方向上有那么一点点分量，就能够一马平川地滑下去．除非分量非常非常小的情况下才可能会继续陷在鞍点附近．换句话说，如果加了一个随机扰动，其实大概率情况下是能够逃离鞍点的！

虽然这个想法也很直观，但是要严格地证明很不容易，因为具体函数可能是很复杂的，Hessian矩阵也在不断地变化，所以要说明＂扰动之后会陷在鞍点附近的概率是小概率＂这件事情并不容易．

想法也很直观，但是要严格地证明很不容易，因为具体函数可能是很复杂的，Hessian矩阵也在不断地变化，所以要说明＂扰动之后会陷在鞍点附近的概率是小概率＂这件事情并不容易．

作者们采取了一个很巧妙的方法：对于负特征值的那个方向，任何两个点在这两个方向上的投影的距离只要大于u/2, 那么它们中间至少有一个点能够通过多跑几步GD逃离鞍点．也就是说，会持续陷在鞍点附近的点所在的区间至多只有u那么宽！通过计算宽度，我们也就可以计算出概率的上届，说明大概率下这个SGD+GD算法能够逃离鞍点了．