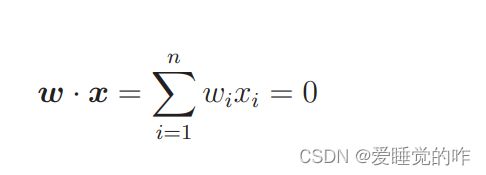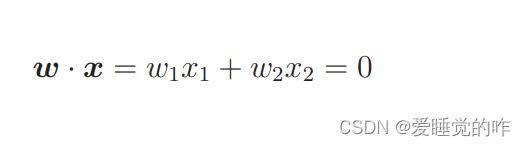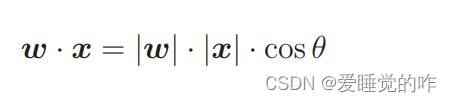机器学习中的数学原理——向量内积

今天是2023年的第一天，祝大家新年快乐！这个专栏主要是用来分享一下我在机器学习中的学习笔记及一些感悟，也希望对你的学习有帮助哦！感兴趣的小伙伴欢迎私信或者评论区留言！这一篇就更新一下《白话机器学习中的数学——向量内积》！

目录

一、什么是内积

二、案例分析 

---

一、什么是内积

内积一般指点积。在数学中，数量积（dot product; scalar product，也称为点积）是接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：a·b=a1b1+a2b2+……+anbn。

二、案例分析 

在上面的学习中，我们已经初步了解了二分类的问题，在最简单的二分类问题中，我们需要找到那条分界线，但是不是像我们之前回归那样，找直线的斜率和截距，而是要找向量。分类用图形来解释更容易理解，所以把它想象为有大小和方向的、 带箭头的向量比较好。

我们所要画的直线是使权重向量成为法线向量的直线。设权重向量为 w，那么那条直线的表达式就是这样的。

我们来慢慢解释上面这段话，权重向量就是我们想要知道的未知参数，w 是权重一词的英 文——weight 的首字母。上次学习回归时，我们为了求未知参数θ 做了很多事情，而 w 和 θ 是一样的。所以它们都是参数，只是叫法不同。上述的表达式就是两个向量的内积,我们也可以写成这样：

我们依然为图像的横纵分类案例举例，图像有宽和高的二维情况， 所以 n = 2 就可以了，表达式就可以写成：

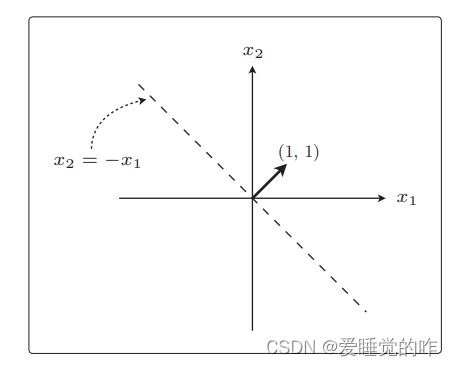
而法线是与某条直线相垂直的向量。我们设权重向量为w = (1, 1)，那么刚才的内积表达式会变成什么样呢？只需要代入(1,1)进行计算就可以了

移项变形之后，表达式变成 x2 = −x1 了。这就是斜率为−1 的直线

在这张图上再画上刚才确定的权重向量 w = (1, 1) 就更容易理解了

权重向量 w 和这条直线是垂直的！这就是“使权重向量成为法线向量的直线”在图形上的解释。高中时我们还学过，用向量之间的夹角 θ和 cos 计算内积的表达式

这是内积的另一个表达式。用这个表达式也没有问题。表达式中 的 |w| 和 |x| 是向量的长，因此必定是正数。所以要想使内积为0，只能使 cos θ = 0。要想使 cos θ = 0，也就意味着 θ = 90◦ 或θ = 270◦ 。这两种情况也是直角。

最终找到与我画的直线成直角的权重向量就完成任务了。

当然，一开始并不存在你画的那种直线，而是要通过训练找到权重向量，然后才能得到与这个向量垂直的直线，最后根据这条直线就可以对数据进行分类了。