第三十五课.基于贝叶斯的深度学习

贝叶斯公式

首先回顾贝叶斯公式：$$p(z|x)=\frac{p(x,z)}{p(x)}=\frac{p(x|z)p(z)}{p(x)}$$通常：

• $p(z)$为先验概率，$z$通常被定义为隐变量；
• $p(z|x)$为后验概率；
• $p(x,z)$为联合概率；
• $p(x|z)$为似然函数；
• $p(x)$为真实分布（evidence）；

引入全概率公式：$$p(x)=\int p(x|z)p(z)dz$$可以将贝叶斯公式改写为：$$p(z|x)=\frac{p(x|z)p(z)}{\int p(x|z)p(z)dz}$$当隐变量$z$是离散型变量时，积分符号改成求和：$$p(z|x)=\frac{p(x|z)p(z)}{\sum p(x|z)p(z)dz}$$

---

通常，使用$P$表示分布函数，$p$表示概率密度函数

---

在常规的神经网络中，对于一个神经元有：

其中，权重$w_i$和偏置$b$都是确定的一个值，在前向推理过程中，缺少了一定的随机性，如果将权重和偏置视为分布，推理时每次从分布中采样出具体的权重和偏置，就得到了基于贝叶斯的深度学习Bayesian neural networks（BNN）。

---

正如过去说过的，贝叶斯理论的核心即：一切皆为随机变量，换言之，一切皆分布

---

下面是一个直观的例子：

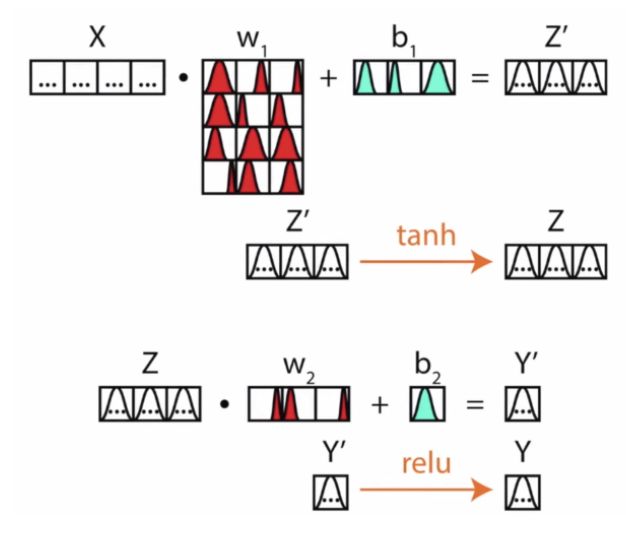
该网络分别有两层参数，即对应两层参数的分布。

基础问题

贝叶斯深度学习与深度学习的区别

在深度学习的基础上把权重和偏置变为分布（distribution）就是贝叶斯深度学习。

贝叶斯深度学习有以下优点：

• 贝叶斯深度学习比非贝叶斯深度学习更加 robust。因为我们可以采样一次又一次，细微改变权重对深度学习造成的影响在贝叶斯深度学习中可以得到解决；
• 贝叶斯深度学习可以提供不确定性（uncertainty）。

贝叶斯神经网络与贝叶斯网络

贝叶斯网络（Bayesian network），又称信念网络（belief network），是有向无环图模型（directed acyclic graphical model），是一种概率图模型（概率图模型的核心是多维随机变量的联合概率分布进行计算）。

贝叶斯神经网络（Bayesian neural network）是贝叶斯和神经网络的结合。

贝叶斯神经网络和贝叶斯网络是两个不同的对象。

关于贝叶斯深度学习的框架，可以参考：BoTorch：

贝叶斯神经网络的推理与学习

前向计算

想要像非贝叶斯神经网络那样进行前向传播，我们可以对贝叶斯神经网络的权重和偏置进行采样，得到一组参数，然后像非贝叶斯神经网络那样使用即可。

当然，我们可以对权重和偏置的分布进行多次采样，得到多个参数组合，参数的细微改变对模型结果的影响就可以体现出来。这也是贝叶斯深度学习的优势之一，多次采样最后一起得到的结果会更加具有鲁棒性。

学习

给定训练集$D=\left\{(x_1,y_1),...,(x_m,y_m)\right\}$，训练贝叶斯神经网络，按照贝叶斯公式有：$$p(w|x,y)=\frac{p(y|x,w)p(w)}{\int p(y|x,w)p(w)dw}$$我们希望得到后验概率$p(w|x,y)$，先验概率$p(w)$是提前设置的（初始化），比如初始时令$p(w)$为标准正态分布。

似然$p(y|x,w)$是一个关于$w$的函数，当$w$等于某个值时，我们便可以确定分子$p(y|x,w)p(w)$，对于分母，要对$w$的取值空间进行积分，但$w\in R$，这是非常复杂的计算，因此需要寻求其他近似方法以计算分母。

对于训练，通常有以下三种方法：

• 用蒙特卡洛采样去近似分母的积分，其本质即为：用采样得到的统计结果去实现近似；
• 直接用一个简单的分布$q$近似后验概率$p$，不再考虑分母的积分，直接基于KL散度最小化$p$和$q$的差异；
• 蒙特卡洛Dropout，简单实用，不改变网络原始结构，只需要在每层网络后加Dropout，训练过程也和常规神经网络一致，只需要在测试时，多次对同一输入前向计算，从而达到引入随机性的目的。