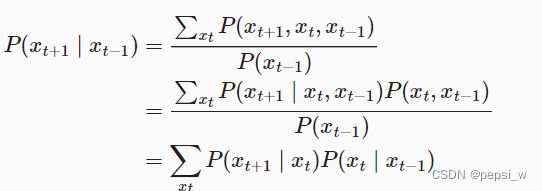9--序列模型

        在现实生活中，很多数据是具有时序结构的，如一段文字、语音等。

9.1 统计工具

        处理序列数据需要统计工具和新的深度神经网络架构。假设某股票在时刻t的价格为xt，则使用t时刻之前的价格来对t时刻的价格进行预估：这里可以使用不同的模型来对xt进行预估。

 9.1.1 自回归模型

        第一种假设在xt只与它之前的个序列相关，即使用观测序列就能预测出xt的值，这样做的好处是保证了在 t > τ 时，参数的数量是固定的，这种模型被称为自回归模型，因为它们是对自己执行回归。

        第二种假设如下图所示，保留一些对过去观测的总结， 并且同时更新预测和总结， 这就产生了基于估计xt， 以及公式更新的模型。 由于ht从未被观测到，这类模型也被称为隐变量自回归模型。

        这两种方法中的训练数据由历史数据组成，整个序列的估值公式如下所示： 

9.1.2 马尔可夫模型 

        使用xt−1,…,xt−τ 而不是xt−1,…,x1来估计xt，只要这种是近似精确的，就说序列满足马尔可夫条件（Markov condition）。 特别是，如果τ=1，得到一个一阶马尔可夫模型：

         对于离散值的计算如下：

9.1.3 使用回归模型来对数据进行预测 

        这里使用简单的MLP模型来对生成的带有噪音的正弦函数值进行训练，将前面4个数据作为特征，第5个数据为label，这样就能通过前面4个值来对xt进行预测。

        实现代码如下：

!pip install git+https://github.com/d2l-ai/d2l-zh@release  # installing d2l
!pip install matplotlib_inline
!pip install matplotlib==3.0.0

import torch
from torch import nn
from d2l import torch as d2l

#生成1000个数据
T = 1000
time = torch.arange(1,T+1,dtype=torch.float32)
#加入噪音
x = torch.sin(0.01*time)+torch.normal(0,0.2,(T,))

tau = 4
#将前四个作为特征值，第五个数作为label，这样就会有1000-4个样本，每个样本的特征维度为4
features = torch.zeros((T-tau,tau))
for i in range(tau):
  features[:,i] = x[i:i+T-tau]#这里很巧妙 可以自己画个简单的来看
labels = x[tau:].reshape((-1,1))

batch_size,n_train = 16,600
#只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train],labels[:n_train]),batch_size=batch_size,is_train=True)


def init_weights(m):
  if type(m)==nn.Linear:
    nn.init.xavier_uniform_(m.weight)

def get_net():
  net = nn.Sequential(nn.Linear(4,10),nn.ReLU(),nn.Linear(10,1))
  net.apply(init_weights)
  return net

loss = nn.MSELoss(reduction='none')

def train(net,train_iter,loss,lr,epoch_num):
  trainer = torch.optim.Adam(net.parameters(),lr)
  for epoch in range(epoch_num):
    for X,y in train_iter:
      trainer.zero_grad()
      l = loss(net(X),y)
      l.sum().backward()
      trainer.step()
    print(f'epoch {epoch+1},'f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')
net = get_net()
train(net,train_iter,loss,0.01,5)

onestep_pred = net(features)
d2l.plot([time,time[tau:]],[x.detach().numpy(),onestep_pred.detach().numpy()],
              'time','x',legend=['data','1-step preds'],figsize=(6,3))

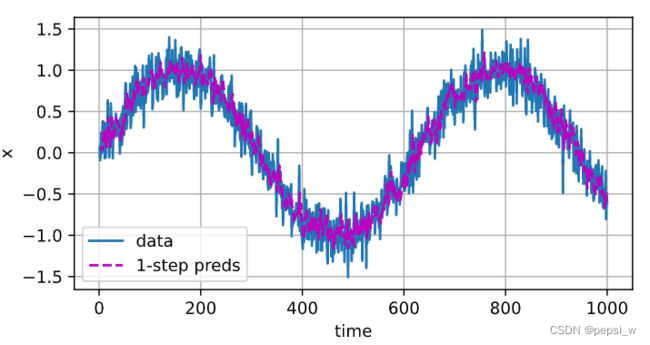
        运行结果如下，左图是整个训练过程中损失函数的变换，可以看出该模型的一个损失值是稍微有点大的。右图中紫色的点就是对所有数据进行预测的结果，预测结果跟实际数据大体走向是一致的。

 

        使用前600个来对整个序列进行预测，并将预测值作为已知数据，并参与对后面的数据进行预测，具体代码如下：

multistep_preds = torch.zeros(T)
multistep_preds[: n_train+tau] = x[: n_train+tau]
for i in range(n_train+tau,T):
  #使用前tau个数来对i进行预测 并将预测结果放回序列中 作为已知值对后面进行预测
  multistep_preds[i] = net(multistep_preds[i - tau:i].reshape((1, -1)))

d2l.plot([time, time[tau:], time[n_train + tau:]],
         [x.detach().numpy(), onestep_pred.detach().numpy(),
          multistep_preds[n_train + tau:].detach().numpy()], 'time',
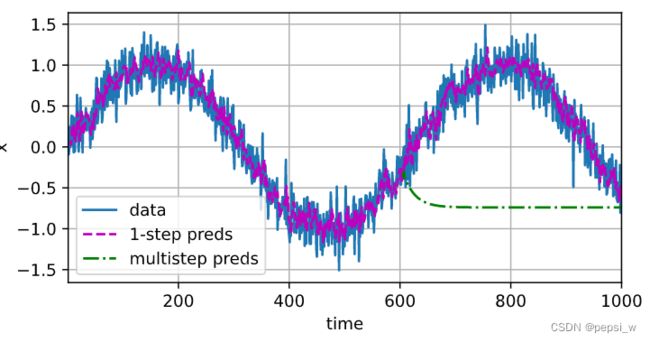
         'x', legend=['data', '1-step preds', 'multistep preds'],
         xlim=[1, 1000], figsize=(6, 3))

        运行结果如下图所示，可以看出600后面的值与真实数据误差很大，这是由于用来预测后面数据的值本身也是一个有误差的预测值，最终误差的累积导致后面数据与真实数据呈现出很大的误差。