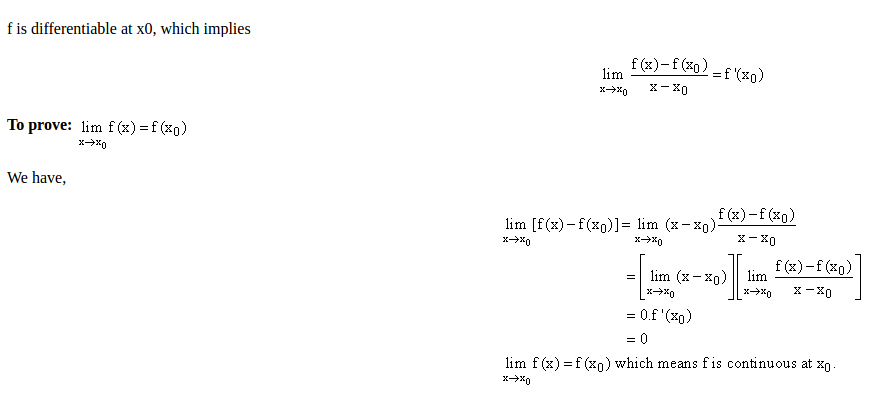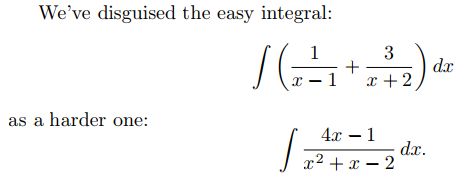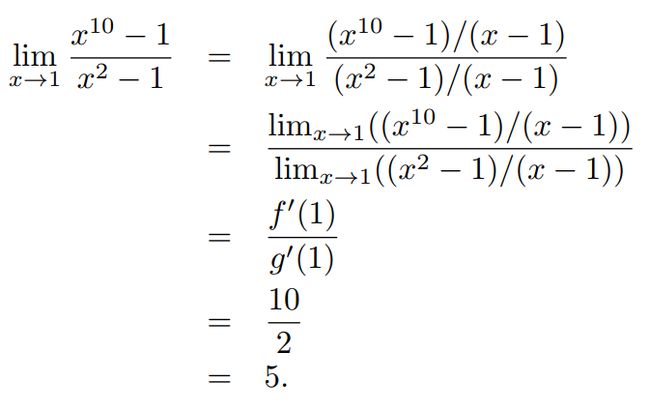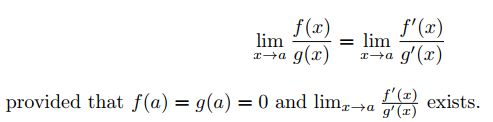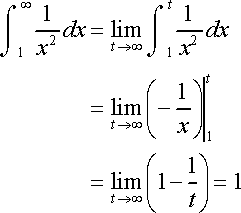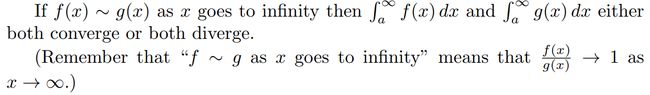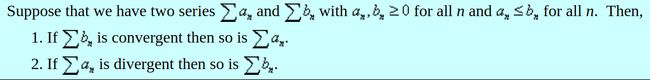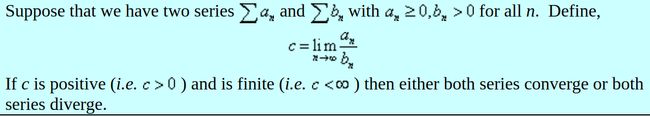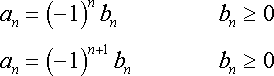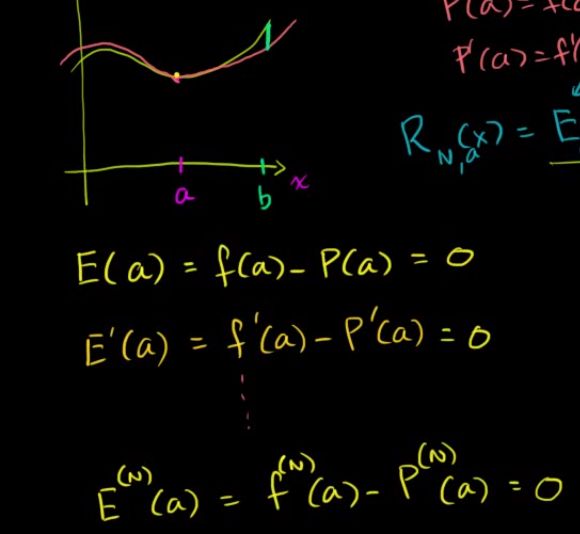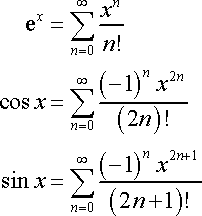MIT 18.01 单变量微积分总结
引言
这篇文章是对 MIT Single Variable Calculus 这个课程的知识点总结。在这个课程中,我遇到一些问题涉及到先前高中学过的知识,同时也有一些比较难理解的或容易混淆的概念,因此我把找到的这些资料链接列在下面(这些资料弥补了我先前忘记的知识,并且加深了对课程内容的理解,非常有帮助):
What is a Function?
Even and Odd Functions
Function Transformations
Inverse function
In what sense is the derivative the “best” linear approximation?
Inflection points introduction
Continuous versus differentiable
How to Detrmine when Limits Don’t Exist
Prove that the derivative of an even differentiable function is odd, and the derivative of an odd is even
limit and continuity
下面是 continuous 的定义:
A function f is continuous at x0 if limx→x0f(x)=f(x0)
如果一个函数在 x0 处是 continuous 的,那么从下面的定义中,我们可以得出以下3个属性:
- limx→x+0f(x)=limx→x−0f(x)
- f(x0) is defined
- limx→x+0f(x)=limx→x−0f(x)=f(x0)
下面中的链接是关于 limit 的一些属性,和证明这些属性为什么是正确的。
Limit Properties
Proof of Limit Properties
下面我们来证明一个定理,定理的内容如下:
If f is differentiable at x0, then f is continuous at x0
如果 f is continuous at x0,我们有 limx→x0f(x)=f(x0) ,因此我们只需要证明,当函数 f 在 x0 处可导,这个等式是成立的。整个证明过程如下图:
sin 与 cos 导数的证明
在这个 lecture 中,David Jerison 教授讲解了 sin 与 cos 函数导数的代数与几何证明,在具体证明之前,让我们首先求出2个极限的解,它们分别是:
我们首先来证明第2个极限,下图是个单位圆,角度 θ is described in radians but NOT when it is measured in degrees.
把第2个极限中的 Δx 用 θ 替换,我们可以看出当 θ 无限接近于0时, sinθ 与 arc length(即 θ )无限接近,因此我们可以总结出:
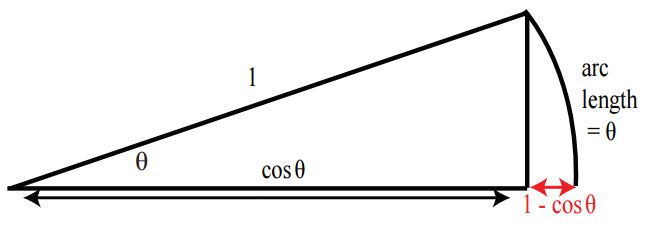
接下来让我们来求第1个极限,下图来自于单位圆的一部分,我们可以看出当 θ 无限接近于0时, 1−cosθ 无限接近接近于0,因此我们可以总结出:
上面的几何证明过程中,有2个重点我需要解释一下:
1、在MIT的课堂上,我看到很多同学会问到:当 θ 无限接近于0时, 1−cosθ 无限接近接近于0,同时 arc length 不也接近于0吗?这里我们忽略了一个重点,就是 1−cosθ 接近于0的速度要比 theta 接近于0的速度快很多。
2、上面极限中的角度全是以弧度来描述的,如果你以度数来描述,则上面的结论不成立,因此当我们对 sinx和cosx 求导时,这些 x 所指的一定要是弧度。
至此,我们已经求出了上面的2个极限。现在,只需要一些代数 tricks 就可以证明出 sinx与cosx 的枯导数,这里我就不介绍了,MIT 给的课程资料上有详细的步骤,下面是资料的链接:
Derivative of sinx
Derivative of cosx
下面我们来用几何的方式去证明 sinx 的导数,导数本身想表达的就是 the rate of change,即 ratio,现在我们来看一看 y=sinθ ,当 θ 增加 Δθ 时, Δy 是多少?
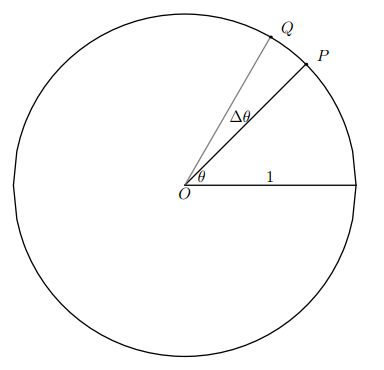
下图是个单位圆,当角度增加 Δθ 时, y 如何变化呢?我们可以把上图中的弧 PQ 单独拿出来,如下图:
当 Δθ 无限小时,我们可以把弧 PQ 近似成上图的绿线,由于 Δθ = 弧 PQ ,所以直线 QP 约等于 Δθ ,现在最重要的就是我们要如何求出角 ∠QPR ,其实它就是 θ ,因此我们可以得出:
General Strategy for Curve Sketching
在这个 lecture 中, Jerison 教授介绍了一个通用的策略去大致描绘出函数图像,下面的链接中给出了具体的步骤,如果步骤1和2中的点很难找出,你可以直接跳到第3步。
描绘函数图像
函数的平均值
想必你已经知道如何求解一个离散集合的平均值,比如: a1,a2,…,an ,那么它的平均值定义如下:
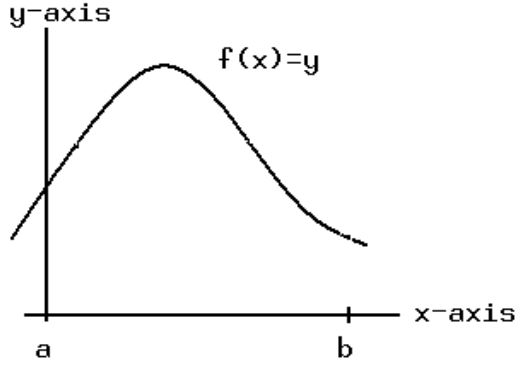
那么现在,我想求出下图中函数在区间 [a,b] 的平均值,我们怎样做到这点呢?
我们目前虽然不知道如何去求连续函数在某一区间的平均值,但是我们会求一个离散集合的平均值,因此我们可以通过这个方法来粗略估计出上图所示函数的平均值,过程如下:
1、Split [a,b] into subintervals width Δx=b−an
2、Pick a point xi in each subinterval
3、Average just the f(xi) :
随着 n n 逐渐增大,上面估算出的平均值将会越接近真正的平均值,感觉有点像积分呢!别要着急,好戏还在后面。
4、把上面的公式中的分子与分母都乖上 \Delta xΔx:
Average \approx \frac{(f(x_1)+f(x_2)+\dots+f(x_n))*\Delta x}{n*\Delta x}
我们可以看出,上面公式中的分子是 Riemann sum,因此随着 n n 逐渐增大,它变成了积分; 由于 \Delta x = \frac{b-a}{n}Δx=b−an,我们有如下式子:
5、取极限
因此,函数 f(x) 在区间 [a,b] 的平均值定义如下:
Fundamental theorem of calculus 告诉我们: ΔF=∫baf(x)dx ,我们把两边同除以 Δx ,并根据上面推导出的定义,得到 ΔFΔx=Average(f) ,重写这个公式,得到如下式子:
由于 mina<x<bf(x)≤Average(f)≤maxa<x<bf(x) ,因此得到如下公式:
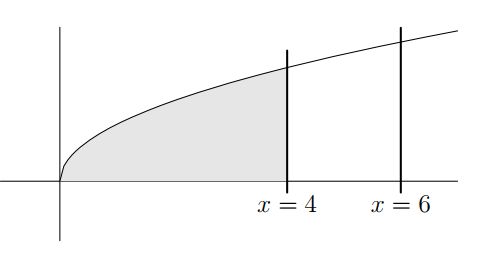
用积分求立方体体积
我下面介绍的这些方法都是求旋转体(solid of revolution)的体积,它们都是由某个平面沿着某个轴旋转得出的不规则立方体。在某些情况下,我们用哪个方法都可以解决问题,但是某个方法可能比另一个方法的计算要容易,但是在另一些情况下,只能用某个方法,而不能用其它方法。
Disk method
假设下图中弧线的公式为 y=f(x) ,我们把这个弧线沿着 x 轴旋转 360 度,如何求出这个旋转之后的体积呢?
我们通过 slicing the solid vertically into disk shaped pieces and summing the volumes of the disks,就可以求出体积了,这个方法没什么好说的,太简单了!
这个 disk 的厚度就是 dx ,底面积就是 πr2 ,其中 r=f(x) ,所以:
然后把 dV 积分就可以求出体积了。
Washer method
我们把下图中阴影部分的面积沿着 x=6 旋转,这回应该如何求出体积呢?我们通过 slicing the solid horizontally into washer shaped pieces and summing the volumes of the washers 就可以求出体积了。
实际上一个 wahser 的体积就是一个大 disk 的体积减掉一个小 disk 的体积, 每个 washer 有一个高度为 dy ,一个 inner radius r,和一个 outer radius R≥r 。所以:
然后把 dV 积分就可以求出体积了。
Shell method
这回我们要求的体积依然是 Washer method 中那个图形旋转过后得到的体积,只不过这次是用 shell method. 在 Washer method 中,我们采用的是 slicing the solid horizontally,这回我们要 slicing the solid vertically,那么在 Shell method 方法中,我们得出的是一个 shell(形状像 cylinder),那么我们如何求出 shell 的体积呢?我们把它展开成一个长方体来求体积,它的长为:半径为 (6-x)的周长; 宽为: dx ; 高为: f(x) . 这里我们应该注意的是,正是由于 dx 非常小,我们才可以把它展开成一个长方体来求面积,如果 dx 很大,那它实际上就是一个 hollow cylinder,而对于一个 hollow cylinder 来说,你根本就不可能把它展开成一个长方体,这是因为 inner radius 和 outer radius 的长度差距很大。
考试题目
考试题目 里面涉及了几个综合的问题,对整个积分与微分的学习非常有帮助。下面我把几个重要的点指出来,方便日后 review:
1、第3题(a):除了答案中给的积分方法,你也可以直接将平方展开,然后对每项分别求和,其中每个项的求和结果分别是3,9,9. 在计算的过程中会遇到 12+22+32+⋯+n2=n(n+1)(2n+1)6 ,Formula For the Sum Of the First N Squares 详细解释了公式的推导过程。
2、第3题(b):这个题目要用 fundamental theorem of calculus 来做,答案给的很简略,我现在补充一下。棘手的地方就是它的积分极限是 [0,x2] ,其实我们可以用替换变量的方法来解决这个难题,过程如下:
让 u=x2 ,令 g(u)=∫u0f(t)dt ,现在让我们求 g(u) 的导数,由于 u 是关于 x 的函数,所以根据 fundamental theorem of calculus 和 chain rule 得到如下过程:
3、第4题(a):当求这种加权平均的问题时,我们可以把要求的变量认为是离散问题中的 1,2,3,4,5. 然后不同的问题一定有一个总体,然后我们可以想像分别把总体切分贡献到上面的1,2,3,4,5上。比如:这个问题中我们要求的是 centroid 的 x,y 坐标,在离散的情况下,x可以是1,2,4,5,5,只不过现在x是连续的,这个问题中的总体是面积,我们把这个面积竖直切割成一个个小部分,然后贡献到对应的 x,当然了千万别忘记最后除以总体,就和离散加权的平均值一样。
其它题目也都非常好,必须要再做一遍。
求解积分的技术
用 Substitution Rule 求解积分通用过程
1、看 integrand 在给定的区间内是否连续?
2、看 integrand 是奇函数或者是偶函数吗?
如果 f(x) 为奇函数: ∫a−af(x)dx=0
如果 f(x) 为偶函数: ∫a−af(x)dx=2∫a0f(x)dx
Note that in order to use these facts the limit of integration must be the same number, but opposite signs!
3、用 Substitution Rule 求解积分
具体步骤参考:Substitution Rule for Definite Integrals
Trigonometric Powers
求下面形式积分的通用过程:
上式中的 m and n are non-negative integers. There are two cases to think about here. The easy case is the one in which at least one exponent is odd. MIT 的教授在课上给了几个这种 case 的例子:
例子1
例子2
例子3
你会发现只要 integrand 有一个是 odd power,我们只需要用 sin2(x)+cos2(x)=1 把那个 odd power 的拆分一下,然后用 substitution 就可以顺利地求出积分。比如:上式中的 n 是奇数的,我们就可以拆分成 sinn−1(x)sin(x),n - 1 就一定是偶数了,所以可以用 sin2(x)+cos2(x)=1 把 sinx 转化成 cosx 了,而这个单独的 sinx 就可以用 substitution 处理,比如令 u=sinx,du=cosxdx
更困难的一种 case 是 m 和 n 都是偶数的。这时我们需要用半角公式 turning even powers of sin x and cos x into odd powers of cos(2x),MIT 的教授给了这种 case 的几个例子:
例子1
例子2
例子3
每当我们看到 the square root of a quadratic in an integral, you should think
of trigonometry and sin2θ+cos2θ ,比如 a2−y2−−−−−−√ ,对于这样的 integrand,我们可以画一个半径为 a 的圆,然后用三角函数 substitute y或x,仔细做下面的2个例子,看它们具体步骤用到的各种技巧:
例子1
例子2
Trigonometric Substitution and Completing the Square
Review of Trigonometric Identities 包含了很重要的三角函数等式,应该推导性地熟记这些公式。下面的链接中分别包含了求 Tangent,Secant,和一些重要三角函数积分的总结:
Integral of Tangent
Integral of Secant
Summary of Trig Integration
对于 square root of a quadratic function 来说,我们要用 trig substitution 来求解这样的积分,下图中是教授总结出的3种基本形式:
一旦你替换完成,你可以使用 Undoing Trig Substitution 去得到最终的答案。有些时候,我们并没有那么幸运得到上面3种基本形式,我们需要 Completing the Square 来把公式重写成上面熟悉的3种形式,下面是2个 Completing the Square 的例子:
例子1
例子2
这是一个 Trig Substitution 的例子:Example of Trig Substitution
Integration by Partial Fractions
Partial Fractions 技术总结来说分为以下3个过程:
- Factor the denominator Q(x)
- Set-up (describe the target sum)
- Cover-up (solve for unknown coefficients)
Partial Fractions 技术主要是求解下面形式的积分:
P(x) and Q(x) are polynomials, functions of this type are called rational functions. 下图中的第一个积分我们可以很容易地求出来,但是第2个积分就不容易,而实际上它们是同一个积分,而 partial fractions 技术就是教我们如何把难的积分变成这个简单的形式,这个方法只有在 x 的指数是整数时使用!
用 partial fractions 求解上面困难形式的积分如下所示:
我们如何用求解上图中的变量 A 和 B 呢?用 Cover-up 方法可以大大加快我们求解的速度。在 Integrate by Partial Fractions 这个例子中,求 A,B,和 C的过程就叫做 Cover-up,我们可以看出它可以非常快速的求出未知变量。
partial fractions 中第2步的 setup 分为如下几种情况:
Repeated Factors
Quadratic Factors
这是一个关于 Quadratic Factors 的例子,希望我认真 review 一下它解题的过程。
注意:只有当 Q(x) 的 degree 大于 P(x) ,你才可以用上面的步骤。反之,你需要用 Long Division 转化一下,然后你可以用 partial fractions,Substitution Rule 或者 Trigonometric Substitution 去求出最后的积分。 这是个关于 Long Division 的 例子
教授也给我们总结出求这样一种有理函数形式积分的整个过程:Partial Fractions – Big Example,仔细 review.
Integration by Parts
下图是公式:
这个教授介绍了几个 Reduction Formula 去求积分,它们分别是如下的积分:
∫(lnx)ndx
∫xnexdx
Integration by reduction formulae 上给出了更多的例子,有空参考一下,尤其是 ∫xncos(x)dx 和 ∫xnsin(x)dx ,下面是一个例子:
例子
L’Hˆopital’s Rule
在我们不会洛必达法则之前,如何求出下面的极限呢?
令 f(x)=x10−1 和 g(x)=x2−1 ,让分子和分母同时除以 x−1 ,得到如下形式:
上面只是一个例子,我们可以用上面的过程得到一个更加通用的例子:
从上面的推导过程可以看出, f(a)=g(a)=0 ,否则我们的推导过程将不成立。洛必达法则内容如下:
总结来说,只有在 00 或 ∞∞ 这样的 case 下,我们才可以应用洛必达法则。仔细看一下整个 lecture 所写的内容,它也给出了不能用洛必达法则的例子,而是用 linear approximation 来解决的,同时这个 lecture 也告诉我们不要过度依赖它。其实我们可以看出当极限包含超越函数时,我们要用洛必达法则,而只包含多项式的时候,我们要进行一些代数变形,然后极限就可以很明了地求出来。下面是一个比较好的例子,希望我仔细看一下:
The Indeterminate Form 0^0
反常积分
下面是反常积分的定义:
An improper integral is a definite integral that has either or both limits infinite or an integrand that approaches infinity at one or more points in the range of integration. Improper integrals cannot be computed using a normal Riemann integral.
从上面的定义可以看出,有2种类型的反常积分,它们分别是:
- either or both limits infinite
- integrand that approaches infinity at one or more points in the range of integration
第一种类型反常积分的求解
下面是一个不错的例子:
我们可以暂时把 ∞ 当作是一个很大的数,然后我们就可以用正常的方式去求解这个积分,然后取极限,过程如下:
这里面有个关于收敛和发散的定义:We will call these integrals convergent if the associated limit exists and is a finite number (i.e. it’s not plus or minus infinity) and divergent if the associated limit either doesn’t exist or is (plus or minus) infinity
对于这种类型的反常积分,如果上下2个极限分别是 +∞ 和 −∞ ,我们可以用下面的公式把它拆分成2部分:
Where c is any number. Note as well that this requires BOTH of the integrals to be convergent in order for this integral to also be convergent. If either of the two integrals is divergent then so is this integral.
既然现在可以求出第一种类型的反常积分了,我们可以得到下面的事实:
如果 a>0 ,那么 ∫∞a1xpdx 是收敛的,当 p>1 ; 是发散的,当 p≤1
上面事实中的本质其实就是说:if an integrand goes to zero fast enough then the integral will converge. How fast is fast enough? If we use this fact as a guide it looks like integrands that go to zero faster than 1x goes to zero will probably converge
MIT 的这个教授为我们推导出上面的事实,证明过程请参考 Integral of 1/(xp)
这是关于整个事实的总结,我必须认真看看:事实的整体总结
第二种类型反常积分的求解
这种类型的反常积分实际上就是 integrand 在整个积分区间存在 singularities at finite values. 我把它分为以下4种情况,每种情况都有相对应的求解方法:
1、integrand 在上极限处不连续
2、integrand 在下极限处不连续
3、integrand 在中间某处不连续
4、integrand 在上极限与下极限都不连续
上面公式中涉及到的 c 可以是任意值。 上面的求解过程其实也没什么难的,只不过都是正常求解积分的流程,然后取相应的极限就行了。
Limit Comparison
对于一些积分来说,它们的求解过程非常繁琐,这时我们可以用 limit comparison 来把它转换成一个更容易求解地积分,从而判断出它是收敛还是发散。Limit comparison 的定义如下:
下面是关于 Limit Comparison 的几个例子:
由于我们已经知道 ∫∞1001xdx 是发散的,所以 ∫∞1001x2+10−−−−−−√dx 也是发散的。
另一个例子:Confirming an Integral Converges
有些 integrands 的增长速度或衰减速度非常快,我们可以用 Ordinary comparison 来判断其是否收敛:例子
关于求解反常积分的总结
当我们求解反常积分时,我们应该看看是否存在无穷,或者一些 singularities,必要时,我们需要把原来的积分拆成几部分。同时我们也可以用 Limit Comparison 来快速的判断积分是否收敛。
序列和级数
Sequences
Sequences 可以用如下3种 notation 表示:
![]()
上面中的 an 通常是一个公式。下图中就是一个 sequence 的例子:
你可以把上图 sequence 中的 formula 看作是一个只可以插入整数的函数 f(n)=n+1n2 ,这是一个很重要的思想,Treating the sequence terms as function evaluations will allow us to do many things with sequences that couldn’t do otherwise. 像函数一样,我们可以 graph 上面的 sequence:
从上图可以看出,随着 n 逐渐增大,sequence terms 越来越接近于0,因此可以说 0 is the limit (or sometimes the limiting value) of the sequence 可以写作如下:
可以看出,上面的 notation 与表达函数极限时的 notation 一样。If limn→∞an exists and is finite we say that the sequence is convergent. If limn→∞an doesn’t exist or is infinite we say the sequence diverges.
像函数一样,sequence 也有相应的 Squeeze Theorem,如下:
文章 中 Example 2 的 b 和 c 是关于判断 sequence 收敛/发散 的好例子。下图中是一些关于 sequence 的 terminology and definitions:
下图中是一个关于 sequence 的定理:
上图中的定理并没有说: if a sequence is not bounded and/or not monotonic that it is divergent. 文章 中 Example 2b 就是这样的一个例子。这个定理也有2个很容易理解的变种:
1、If {an} is bounded above and increasing then it converges
2、If {an} is bounded below and decreasing then it converges
Series
级数实际上就是 the sum of a sequence of terms. 比如现在有一个序列为 a1,a2,…,an ,那么级数就是 Sn=∑an ,说得更直接一点就是:序列是一系列的有序的数,而级数就是一个数。因此一定要明白级数的收敛/发散与序列的收敛/发散之间的差异和关系。下面是一个关于它们之间关系的定理:
上面的定理说明如果一个级数收敛,那么它所对应的序列也一定收敛,反之,不成立。 因此,通过这个定理,可以得到 Divergence Test:
If limn→∞an≠0 then ∑an will diverge.
注意:Divergence Test only says that a series is guaranteed to diverge if the series terms don’t go to zero in the limit. If the series terms do happen to go to zero the series may or may not converge!
conditionally convergent 和 absolutely convergent
1、A series ∑an is said to converge absolutely if ∑|an| also converges.
2、If ∑an converges and ∑|an| diverges the series ∑an is called conditionally convergent.
文章 中介绍了一个关于 rearrangement 的概念,其中作者举个关于它的例子,这个例子大致就是说:当我们 rearrange 级数的这些 term 时,得到 sum 有可能不同。关于 conditionally convergent 和 absolutely convergent 有如下事实:
其实上面的事实主要就是说:当一个级数为 absolutely convergent 时,我们可以把 infinite series 看作是 infinite sum,这是由于当 rearrange term 时,产生的结果并不变; 另一方面,当一个级数为 conditionally convergent 时,我们不可以把 infinite series 看作是 infinite sum.
index shift
比如对于下面的级数 ∑∞n=2n+52n 来说,它的 start index 为2,如果让它变成 start index 为0呢?你可以用替代方法,比如让 i=n−2 ,然后 n=i+2 ,之后你就把 i 代入公式中就可以得到想要的结果了,这篇文章的中间部分左右有详细的代入过程。实际上,主要的思路就是:你要让 index shift 之后的级数与之前级数的每项要完全相同。
3个 Special Series
通常情况下,得到一个级数的值是非常困难的(当然了,这个级数要收敛),因此在整个单变量微积分的课程中,下面介绍的2个 series 是唯一可以找到值的,其中1个是发散的。
Geometric Series
在文章的后半部分,我会详细介绍 Power Series,你会发现,Geometric Series 只是 Power Series 的一个特例。它记作如下形式:
这里面有个收敛半径的概念,在 Power Series 的章节中我会详细介绍,这里你只需要知道,如果要让上面的公式成立, |r|<1 . 还有一点需要注意的是,如果你想用这个公式去求 Geometric Series 的值,一定要保证你所求的 series 的形式要与上面公式左面的 series 形式保持一致,必须时,需要做一些变换。
有些时候,我们需要把函数用级数来表示,通过把函数转变成上面函数的形式,找出 a 和 r,就可以用几何级数来表示函数了。文章中的例子2和5是两个不错的例子。
Telescoping Series
Telescoping Series 之所以可以求出值是因此它可以要把中间的 terms 全部约掉,从而只留下头部 term 和尾部 term,因此我们就可以很容易得到 series 的值了。文章 中的例子 3 和 4 都是非常好的例子。
Harmonic Series
Harmonic Series 的形式如下:
用 Integral Test 就可以很容易地证明它是发散的。
判断级数是否收敛
Integral Test
Integral Test 主要就是用 Riemann sum 把级数与反常积分关联起来,我们可以相对容易地判断出反常积分是否收敛,一旦知道反常反常积分是否收敛以后,就可以判断出级数是否收敛。Integral Test 的内容如下:
Suppose that f(x) is a continuous, positive and decreasing function on the interval [k,∞) and that f(n)=an then, ∫∞1f(x)dx 与 ∑∞n=kan 的收敛与发散一致。
下面是做 Integral Test 所需要的条件:
In order to use the Integral Test the series terms MUST eventually be decreasing and positive. If they are not then the test doesn’t work. Also remember that the test only determines the convergence of a series and does NOT give the value of the series
详细的证明过程请参考:Proof of Integral Test,我们可以看到整个证明过程占的篇幅很大,但是思路非常简单,假设我现在想证明的级数是 ∑∞n=1an
1、首先让函数 f(n)=an
2、写出这个函数的 Right Riemann sum 或者 Left Riemann sum,其中让 Δx=1
3、你会发现 Riemann sum 就是级数,然后你用这个函数的反常积分与 Riemann sum 相比较
现在我们已经把反常积分与级数的收敛与否关联起来,并且在这篇文章上面的章节中的引用块中给出了一个总结,因此我们可以给出下面的总结,它被叫做 p-series test:
如果 k>0 ,那么 ∑∞n=k1np 是收敛的,当 p>1 ; 是发散的,当 p≤1
例子:如何用 Integral Test 来判断 harmonic series 是否收敛:文章 的开篇给出了详细的步骤。
Comparison Test 和 Limit Comparison Test
下面是 Comparison Test 所包含的内容:
这篇文章 中的 Example 2 是一个关于 Comparison Test 的非常好的例子,必须好好看看。
其实上面的内容是很直观的,也就说:对于一大一小的2个级数,如果大的级数收敛,那么小的级数必然收敛; 如果小的级数发散,那么大的级数也就必然发散。但是,如果大的级数发散,你就不能断定小级数的行为; 同样地,如果小的级数收敛,你也不能断定大级数的行为。那么在这样的情况下,所以我们才需要 Limit Comparison Test,它的内容如下:
实际上,Limit Comparison Test 只是 Comparison Test 的一个变种,看一下它的证明你就知道为什么了。Proof of Limit Comparison Test
这篇文章 中的 Example 3 是一个关于 Limit Comparison Test 的非常好的例子,必须好好看看。你要仔细注意一下它们是谁除以谁,如果反过来以后,你就会找不出它们比值的极限; 同时你也要注意,要想 Limit Comparison Test 成功,它们的比值的极限必须为常数。
其实你会发现,关于级数的 Limit Comparison Test 与文章上面关于反常积分的 Limit Comparison 的思想是一样的。
Alternating Series Test
从名字就可以看出来,Alternating Series Test 是针对于 Alternating Series 的,那么什么是 Alternating Series 呢?An alternating series is any series, ∑an for which the series terms can be written in one of the following two forms :
当然了,还有很多其它形式的 alternating sign,它们都可以转换成上面的2种形式,比如下图中的2种 alternating sign:
Alternating Series Test 的定义如下:
关于这个 Alternating Series Test 有3点需要注意:
1、它只告诉我们级数什么时候收敛,但是并没有告诉我们级数什么时候发散。也就是说,如果我们有一个级数不满足上面的条件,你需要另寻其它的 test 来验证级数是否收敛或发散。
2、我们只需要 series terms, bn will be eventually decreasing. The point of all this is that we don’t need to require that the series terms be decreasing for all n. We only need to require that the series terms will eventually be decreasing since we can always strip out the first few terms that aren’t actually decreasing and look only at the terms that are actually decreasing. 文章中的 Example 3 就是这样的一个例子。
3、想要判断是否为递减序列,你不能靠直觉,而是应该用导数来检查
Ratio Test
Notice that in the case of L=1 the ratio test is pretty much worthless and we would need to resort to a different test to determine the convergence of the series.
文章中的例子5是一个很好的例子。
Root Test
As with the ratio test, if we get L=1 the root test will tell us nothing and we’ll need to use another test to determine the convergence of the series. Also note that if L=1 in the Ratio Test then the Root Test will also give L=1
这些测试方法的总结
有了这么多的 test 工具,我们应该去认真理解它们的应用条件,有可能多个 test 应用到一个级数上,但是只有一个是最容易得到结果的,因此我们只有通过不断地练习,找出一定的感觉,从而在见到一个级数以后就可以找出最合适的 test. 下面的 guidelines 是一个老外总结出来的,当我做练习的时候,我应该按照这个步骤去找级数的收敛/发散,从而给自己形成一定的感觉。
Again, remember that these are only a set of guidelines and not a set of hard and fast rules to use when trying to determine the best test to use on a series. If more than one test can be used try to use the test that will be the easiest for you to use and remember that what is easy for someone else may not be easy for you!
详细内容请参考:Strategy for Series
Power Series
Power Series 记作如下形式:
上式中的 cn are often called the coefficients of the series. The first thing to notice about a power series is that it is a function of x. 在上面我介绍的级数中,我们只允许 numbers in the series; 而现在,we are allowing variables to be in the series as well. This will not change how things work however. Everything that we know about series still holds.
由于现在有了变量 x 的加入,Power Series 是否收敛,将会取决于变量 x 的值,对于一些 x 有可能收敛,而对于另一些 x 则有可能发散。
存在一个数 R ,如果 |x−a|>R 将使 Power Series 发散,如果 |x−a|<R 将使 Power Series 收敛。这个数 R 叫做这个级数的 radius of convergence. 当 |x−a|=R 时,级数有可能收敛,也有可能发散。
当我们知道 R 以后,我们就可以知道 x 的区间范围,使级数收敛的 x 的范围叫做 interval of convergence. 不仅如此,如果我们想要完全知道这个区间,也需要知道端点处的 x 使级数是否收敛,即, x=a−R 和 x=a+R 处。
无论如何,Power Series 在 x=a 处一定收敛,The series may not converge for any other value of x ,but it will always converge for x=a,这是因此当你把 x=a 插入到 Power Series 中,你会得到如下过程:
文章中的例子1就是一个关于用 ratio test 找出 radius of convergence 的例子
例子3和例子4是两个比较极端的例子,值得一看。对于这2个例子的总结是:If the power series only converges for x=a , then the radius of convergence is R=0 and the interval of convergence is x=a. Likewise if the power series converges for every x the radius of convergence is R=∞ and interval of convergence is −∞<x<∞
介绍 Taylor 与 Maclaurin polynomials
Taylor polynomials 就是 approximating functions 的一种手段。记得先前我已经学过了 linear approximation 和 quadratic approximation 来 approximating functions,但是有了 Taylor polynomials 以后,我们可以用更高阶的多项式来 approximate 函数,阶数越高,approximate 的越准确。
假设我想用 Taylor polynomials 来 approximate 函数 f(x)=ex 在 x=0 处,得到的 Taylor polynomials 暂且称为 P(x) . 那么它的主要思想过程如下:
1、让 f(0)=P(0) ——> P(x)=1
2、让 f′(0)=P′(0) ——> P(x)=1+x
3、让 f′′(0)=P′′(0) ——> P(x)=1+x+12x2
4、让 f′′′(0)=P′′′(0) ——> P(x)=1+x+12x2+16x3
5、keep going …
点击我 演示更多的 approximation.
从上面的过程也可以看出,阶数越高,approximate 的越准确。相信从上面的过程中,你也看出了模式,因此现在可以得出 Maclaurin series 了:
上面的过程我们是在 x=0 处的 approximate,Taylor series 可以让我们在任何一点 approximate,假设在 x=c 处,它的公式如下:
还有一点关于 Taylor polynomial 的重点就是,The nth degree Taylor polynomial may actually have a degree that is less than n. It will never be more than n, but it can be less than n. 文章中的例子3 用到了这个知识,这道题目的大致思路如下:
1、第一种方法也是最容易想到的方法就是求导,然后插入到 Taylor Series 公式中,但是这样的计算量很大。
2、第二种方式就是,分别用相应的 Taylor Series 去替换 ex 和 cos(x) ,这样会得到一个级数的乘法。这个题目让我们给出 Taylor Series 的前3个非零项,正常情况下,degree 为 0,1,2,…,n ,但是有可能存在零项,导致某个 degree 就不存在了,因此我们只需要依次地从2个级数的乘法中找各个 degree,如果其中某个 degree 不存在,则找下个 degree,直到找出3个非零项为为止。找 degree 的过程用乘法分配率就行,谁分配谁无所谓,思路其实很简单。
Taylor polynomial remainder
下图中, f(x) 是原函数,而 P(x) 是 f(x) 在 x=a 处的 Taylor polynomial approximation. 现在,我们想要知道原函数与 Taylor polynomial 之间在 x=b 处的误差,因此误差函数可以写成如下形式:
上式中的 N 为 polynomial 的 degree,a 表示在 x=a 处的 approximation. 还有,我们在上面已经看到了 Taylor polynomial 的过程,所以我们可以得到下图中的那些公式,即 E(a)=f(a)−P(a)=0 等。
图片来源
由于我们已经知道了 degree 为 N , 在 x=a 处,为了使公式变得更加简洁,对于下面所有关于这个主题的公式我都不带下标 a 和 N 了!
现在,分别对上面的误差公式求第 N+1 次导数,由于我们的 degree 为 N ,所以 P(N+1)(x)=0
显然, f(N+1)(x) 是可以被 bound 的,由于我们想找出 x=b 处的误差,所以让 x∈[a,b] ,那么在这个范围内,设最大的 f(N+1)(x) 值为 M ,所以有如下公式:
通过对上面取积分,我们就可以得到 |R(x)| 的边界了,下图中是详细的过程,其中的 E(x)=R(x) ,通过上面我们的推导,可知下图中的 M=Max(f(N+1)(x)) ,其中 x∈[a,b] ,在这个例子中,我们让这个区间为 [a,b] ,但是,我要知道,在任何一个问题中,只要区间包含 center 和 要求的 x 就行,这个例子中的 center 和 x 分别为 a 和 b,所以区间 [a,b] 符合要求。
文件 中的5,6页有2个关于找出误差边界的例子。
下图中是3个比较重要函数的 Taylor series 表示,文章中有详细的推导过程。通过上面的学习,我们都知道 Taylor polynomials 是 approximate 函数,想要下面3个式子相等,我们需要证明 f(x) 与 P(x) 之间的误差为0,即需要证明 limn→∞R(x)=0 ,这个证明过程很复杂,我们假设它成立,才有下面的等式。