理解Markov, Chebyshev, Chernoff概率不等式
Markov inequality
若Y是非负随机变量,对于所有 y > 0 \displaystyle y >0 y>0,都有
P r { Y ≥ y } ≤ E [ Y ] y \mathrm{Pr}\{Y\geq y\} \leq \frac{\operatorname{E}[ Y]}{y} Pr{Y≥y}≤yE[Y]
如上图, y P r { Y ≥ y } \displaystyle y\mathrm{Pr}\{Y\geq y\} yPr{Y≥y}是阴影部分的面积,而整个曲线下的面积是均值,所以,显然 y P r { Y ≥ y } ⩽ E [ Y ] \displaystyle y\mathrm{Pr}\{Y\geq y\} \leqslant E[ Y] yPr{Y≥y}⩽E[Y]。
事实上,这个曲线下面积是均值只有在Y是非负随机变量才能成立,我们可以来验证一下:
P r { Y ≥ y } = 1 − F ( y ) \mathrm{Pr}\{Y\geq y\} =1-F( y) Pr{Y≥y}=1−F(y)
其中 F ( y ) : = P ( Y ⩽ y ) \displaystyle F( y) :=P( Y\leqslant y) F(y):=P(Y⩽y)是Y的累计分布函数,满足 F ( + ∞ ) = 1 \displaystyle F( +\infty ) =1 F(+∞)=1,于是
∫ 0 + ∞ P r { Y ≥ y } d y = ∫ 0 + ∞ ( 1 − F ( y ) ) d y = y ( 1 − F ( y ) ) ∣ 0 + ∞ + ∫ 0 + ∞ y f ( y ) d y = E [ y ] \int ^{+\infty }_{0}\mathrm{Pr}\{Y\geq y\} dy=\int ^{+\infty }_{0}( 1-F( y)) dy=y( 1-F( y)) |^{+\infty }_{0} +\int ^{+\infty }_{0} yf( y) dy=E[ y] ∫0+∞Pr{Y≥y}dy=∫0+∞(1−F(y))dy=y(1−F(y))∣0+∞+∫0+∞yf(y)dy=E[y]
显然,y不是非负的时候,积分可以取到 − ∞ \displaystyle -\infty −∞,这时候 y ( 1 − F ( y ) ) \displaystyle y( 1-F( y)) y(1−F(y))就会发散,不再等于0了。
Chebyshev inequality
既然Markov inequality只能用于非负变量,那对于那些可以取负值的随机变量咋办?其实我们可以对随机变量取平方或者绝对值让他变成非负的,最典型的做法是,令 Y = ( Z − E [ Z ] ) 2 \displaystyle Y=( Z-E[ Z])^{2} Y=(Z−E[Z])2,这时候Y就是一个非负随机变量了,于是
P r { ( Z − E [ Z ] ) 2 ≥ y } ≤ E [ ( Z − E [ Z ] ) 2 ] y = σ z 2 y \mathrm{Pr}\left\{( Z-E[ Z])^{2} \geq y\right\} \leq \frac{\operatorname{E}\left[( Z-E[ Z])^{2}\right]}{y} =\frac{\sigma ^{2}_{z}}{y} Pr{(Z−E[Z])2≥y}≤yE[(Z−E[Z])2]=yσz2
我们将 y \displaystyle y y换成 ϵ 2 \displaystyle \epsilon ^{2} ϵ2,于是 ( Z − E [ Z ] ) 2 ≥ ϵ 2 ⟹ ∣ Z − E [ Z ] ∣ ⩾ ϵ \displaystyle ( Z-E[ Z])^{2} \geq \epsilon ^{2} \Longrightarrow |Z-E[ Z] |\geqslant \epsilon (Z−E[Z])2≥ϵ2⟹∣Z−E[Z]∣⩾ϵ,于是
P r { ∣ Z − E [ Z ] ∣ ≥ ϵ } ≤ σ z 2 ϵ 2 \mathrm{Pr}\{|Z-E[ Z] |\geq \epsilon \} \leq \frac{\sigma ^{2}_{z}}{\epsilon ^{2}} Pr{∣Z−E[Z]∣≥ϵ}≤ϵ2σz2
这就是Chebyshev inequality. 而且当 Z = ( X 1 + . . . + X n ) / n \displaystyle Z=( X_{1} +...+X_{n}) /n Z=(X1+...+Xn)/n表示样本均值的时候,该不等式可以被用来证明weak law of large numbers.
Chernoff bounds
显然,除了平方和绝对值之外,指数函数也是一个非负函数,所以当 Y = e Z r \displaystyle Y=e^{Zr} Y=eZr时,
P r { e Z r ≥ y } ≤ E [ e Z r ] y \mathrm{Pr}\left\{e^{Zr} \geq y\right\} \leq \frac{\operatorname{E}\left[ e^{Zr}\right]}{y} Pr{eZr≥y}≤yE[eZr]
如果我们用 e r b \displaystyle e^{rb} erb来代替 y \displaystyle y y会更有意义。注意到,当 e Z r ⩾ e r b \displaystyle e^{Zr} \geqslant e^{rb} eZr⩾erb时。若 r > 0 \displaystyle r >0 r>0则等价于 Z ⩾ b \displaystyle Z\geqslant b Z⩾b,否则 Z < b \displaystyle Z< b Z<b. 因此,对于任意的实数b,我们有
P r { Z ≥ b } ≤ E [ e Z r ] e r b r > 0 P r { Z ≤ b } ≤ E [ e Z r ] e r b r < 0 \begin{array}{ c c c } \mathrm{Pr}\{Z\geq b\} \leq \frac{\operatorname{E}\left[ e^{Zr}\right]}{e^{rb}} & & r >0\\ \mathrm{Pr}\{Z\leq b\} \leq \frac{\operatorname{E}\left[ e^{Zr}\right]}{e^{rb}} & & r< 0 \end{array} Pr{Z≥b}≤erbE[eZr]Pr{Z≤b}≤erbE[eZr]r>0r<0
它的最重要应用是当Z是 S n = X 1 + . . . + X n \displaystyle S_{n} =X_{1} +...+X_{n} Sn=X1+...+Xn独立同分布样本的求和的时候,我们有
P r { S n ≥ n a } ≤ E [ e S n r ] e r n a = E [ e X r ] n e r n a r > 0 P r { S n ≤ n a } ≤ E [ e S n r ] e r n a = E [ e X r ] n e r n a r < 0 \begin{array}{ c c c } \mathrm{Pr}\{S_{n} \geq na\} \leq \frac{\operatorname{E}\left[ e^{S_{n} r}\right]}{e^{rna}} =\frac{\operatorname{E}\left[ e^{Xr}\right]^{n}}{e^{rna}} & & r >0\\ \mathrm{Pr}\{S_{n} \leq na\} \leq \frac{\operatorname{E}\left[ e^{S_{n} r}\right]}{e^{rna}} =\frac{\operatorname{E}\left[ e^{Xr}\right]^{n}}{e^{rna}} & & r< 0 \end{array} Pr{Sn≥na}≤ernaE[eSnr]=ernaE[eXr]nPr{Sn≤na}≤ernaE[eSnr]=ernaE[eXr]nr>0r<0
你会发现,在这个bound中,r的取值是任意的,我们可以去搜索所有的r可能的取值来找到一个最紧的bound,而显然r的最优取值是跟a有关的,那么这个最优值是多少呢?注意到 g X ( r ) : = E [ e X r ] \displaystyle g_{X}( r) :=\operatorname{E}\left[ e^{Xr}\right] gX(r):=E[eXr]其实是一个moment generating function(MGF),即, g X ′ ( r ) = E [ X ] , g X ′ ′ ( r ) = E [ X 2 ] \displaystyle g_{X} '( r) =E[ X] ,g_{X} ''( r) =E\left[ X^{2}\right] gX′(r)=E[X],gX′′(r)=E[X2],进一步令 γ X ( r ) : = ln g X ( r ) \displaystyle \gamma _{X}( r) :=\ln g_{X}( r) γX(r):=lngX(r),于是
P r { S n ≥ n a } ≤ e n γ X ( r ) − r n a r > 0 P r { S n ≤ n a } ≤ e n γ X ( r ) − r n a r < 0 \begin{array}{ c c c } \mathrm{Pr}\{S_{n} \geq na\} \leq e^{n\gamma _{X}( r) -rna} & & r >0\\ \mathrm{Pr}\{S_{n} \leq na\} \leq e^{n\gamma _{X}( r) -rna} & & r< 0 \end{array} Pr{Sn≥na}≤enγX(r)−rnaPr{Sn≤na}≤enγX(r)−rnar>0r<0
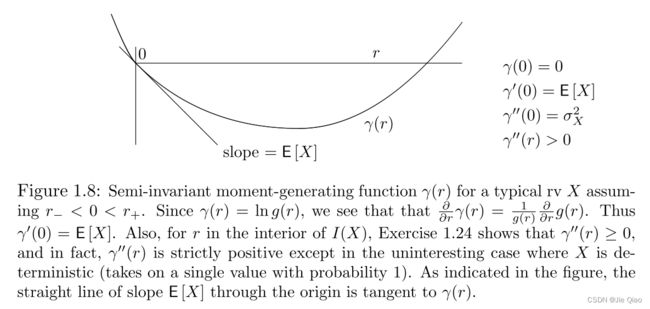
于是,最紧的bound应该就是 n γ X ( r ) − r n a \displaystyle n\gamma _{X}( r) -rna nγX(r)−rna所能取得的最小值。这个取了log之后的MGF又称为cumulant-generating function,它跟MGF的不同在于,它 r = 0 \displaystyle r=0 r=0处的一阶跟二阶cumulant分别对应的是均值和方差。可以证明 γ ′ ′ \displaystyle \gamma '' γ′′是大于0的,是凸函数,可以用方差总是大于0来直观理解。
那么如果 γ X ( r ) \displaystyle \gamma _{X}( r) γX(r)是一个凸函数,整个函数也是凸的,最小值将在极值点上,且关于r的导数为0。那么关于 γ X ( r ) \displaystyle \gamma _{X}( r) γX(r)长什么样呢?如下图
于是最紧的bound是
d ( n γ X ( r ) − r n a ) d r = n γ X ′ ( r ) − n a = 0 \frac{d( n\gamma _{X}( r) -rna)}{dr} =n\gamma '_{X}( r) -na=0 drd(nγX(r)−rna)=nγX′(r)−na=0
这个方程的解,即 γ X ′ ( r ) = a \displaystyle \gamma '_{X}( r) =a γX′(r)=a,于是,我们只要找到个合适的r,其对应位置的斜率为a就是最优的r值了:
参考资料
Gallager, Robert G. “Discrete stochastic processes.” OpenCourseWare: Massachusetts Institute of Technology (2011).
https://www.probabilitycourse.com/chapter6/6_1_3_moment_functions.php