期末C++算法的MATLAB实现
关于计算多重积分的蒙特卡罗法
MATLAB代码:
clc;clear
%蒙特卡洛算法求解圆周率近似值
% 参数初始化:投放10000个点,圆半径为1,圆心坐标(0,0)
% 初始时还未投放点,有0个点在圆内
p = 10000; r = 1; x0 = 1; y0 = 1; n = 0;
% 将p个点随机放在一个边长为2的正方形内,该正方形内有个内切圆
% 正方形的面积是4
% 因为每个点都是“随机投放”的,最终落在圆内的点数比上总点数,就近似等于圆的面积比上正方形面积
% 即2*pi*(r^2)/4 = (圆内点数)/(总点数)
hold on % 保持绘图窗口,多次绘图
for i = 1:p % 对于要投放的总共p个点
% rand函数产生在(0, 1)之间的随机数;rand函数还有其他多种形式,可自行百度
px = rand*2; % 随机生成该点的横坐标
py = rand*2; % 随机生成该点的纵坐标
% 所以,
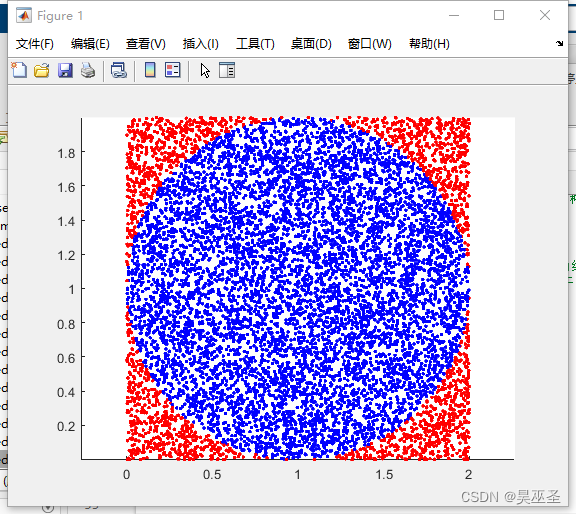
% 若该点在圆内,则颜色设为蓝色,变量n加一;在圆外则设为红色
if (px-1)^2 + (py-1)^2 < 1 % 横纵坐标的平方和小于半径,则在圆内
plot(px,py,'.','Color',"b");
n = n+1;
else
plot(px,py,'.','Color',"r");
end
end
axis equal % 绘图时横纵坐标单位长度相同,便于观察圆
s = (n/p)*4;
pi0 = s;
% 注意:matlab本身有圆周率值,在计算时直接调用pi即可
% a = 2*pi
运算截图:
积分一步的变步长欧拉方法
MATLAN代码:
clear;
format long;
a = 0;
b = 1;
h = 0.1;
d = 1;
res = forward(a, b, h, d);
x = res(1,:);
y = res(2,:);
z = [1, 1.0954, 1.1832, 1.2649, 1.3416, 1.4142, 1.4832, 1.5492, 1.6125, 1.6733, 1.7321];
y(2,:) = z;
plot(x, y);
function result = forward(a, b, h, y)
n = (b-a)/h;
x0 = a;
x1 = a;
y0 = y;
result(1,1) = x0;
result(2,1) = y0;
for m = 0:n-1
x1 = x1 + h;
f0 = y0 - 2*x0/y0;
d = y0 + h*f0;
f1 = d - 2*x1/d;
y1 = y0 + h/2*(f0+f1);
x0 = x1;
y0 = y1;
result(1, m+2) = x0;
result(2, m+2) = y0;
end
end
运算截图: