Pytorch实战-logistic 回归二元分类代码详细注释

 

1、logistic 回归介绍
logistic 回归是一种广义线性回归 (generalized linear model)，与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 wx+b，其中 w 和 b 是待求参数，其区别在于他们的因变量不同，多重线性回归直接将 wx+b 作为因变量，即 y=wx+b，而 logistic 回归则通过函数L 将 wx+b 对应一个隐状态 p, p = L(wx+b), 然后根据 p 与 1-p 的大小决定变量的值。如果 L 是logistc 函数，就是 logistic 回归，如果 L是多项式函数就是多项式回说的更通俗一点，就是 logistc 回归会在线性回归后再加一层 logistic 函数的调用。
logistic 回归主要是进行二分类预测，我们在激活函数时候讲到过 Sigmod 函数， Sigmod 函数是最常见的 logistc 函数为 Sigmod 函数的输出的是是对于 0-1 之间的概率值，当概率大于 0.5预测为 1，小于 0.5 预测为 0。


2、数据集

德国信用数据集：UCI German Credit
https://archive.ics.uci.edu/ml/machine-learning-databases/statlog/german/

3、代码实战

# 导入相关的包

import torch # torch 是一种科学计算框架
import torch.nn as nn # torch.nn 神经网络的接口
import numpy as np # numpy 科学计算的软件包
torch.__version__ # 查看 torch 的版本

# 使用 numpy 的 load 方法读取数据

data = np.loadtxt("german.data-numeric")

注：
numpy 中的 loadtxt() 函数可以用来读取文件，主要是 txt 文件；

# 对数据做一下归一化处理

n, l = data.shape
for j in range(l-1):
    meanVal = np.mean(data[:, j])  
    stdVal = np.std(data[:, j])  
    data[:, j] = (data[:, j]-meanVal) / stdVal

注：

• n, l = data.shape --读取 data 的大小；n 代表行数，l 代表列数

实例：

• data[:, j] --读取 data 所有行的 j 列的数

实例：

• meanVal = np.mean(data[:, j]) # 求 data 所有行 j 列所有数的平均值
• stdVal = np.std(data[:, j]) # 求 data 所有行 j 列所有数的方差
• data[:, j] = (data[:, j]-meanVal)/stdVal # 归一化

# 打乱数据

np.random.shuffle(data)

注：
shuffle() 方法将序列的所有元素随机排序，但 shuffle() 是不能直接访问的，需要导入 random 模块，然后通过 random 静态对象调用该方法。

# 区分训练集和测试集

由于这里没有验证集，所以我们直接使用测试集的准确度作为评判好坏的标准
区分规则：900条用于训练，100条作为测试训练

train_data = data[: 900, : l-1] # 训练试集
train_lab = data[: 900, l-1] -1 # 训练标签
test_data = data[900: , : l-1] # 测试集
test_lab = data[900: , l-1] - 1 # 测试标签

注意：
这里为什么需要在 label 中 -1 呢？
打开原始数据看一下就明白了，主要原因是原始的数据标签范围是1和2，而在代码中使用的是sigmoid函数，其对应的范围是 0-1，因此需要把原始的 label-1.

# 定义模型

class LR(nn.Module):
    def __init__(self):  # 构造函数
        super(LR,self).__init__() # 继承父类的构造方法，等价于 LR.__init__(self)
        self.fc = nn.Linear(24, 2) 
    
    # 定义前向传播函数
    def forward(self,x):
        out = self.fc(x) 
        out = torch.sigmoid(out)
        return out 

注：

• nn.Linear(24, 2) --- 对输入的数据进行线性变换 y = x + b

原型: torch.nn.Linear(in_features, out_features, bias=True)
参数: in_features -- 输入样本数据的大小
out_features -- 输出样本数据的大小；
bias -- 如果设置为 False，则该图层将不会学习加法偏差。默认值：True

参考 :https://pytorch.org/docs/master/nn.html#torch.nn.Linear

# 测试集上的准确率

def test(pred,lab):
    t = pred.max(-1)[1] == lab
    return torch.mean(t.float())

注：

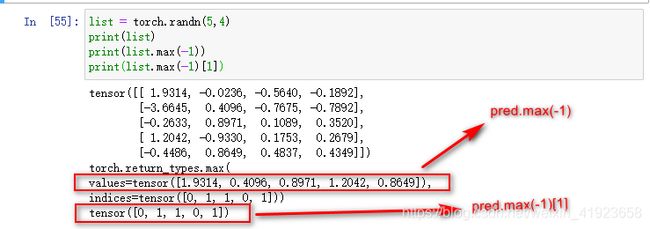
• pred.max(-1) --- 表示取 pred 每一行的最大值；
• Pred.max(-1)[1] --- 表示取 pred 每一行最大值的索引；

实例：

参考：https://blog.csdn.net/jzwong/article/details/103267516

• t = pred.max(-1)[1] == lab --- 返回的是一个长度为样本个数的 0，1 向量
• torch.mean(t.float()) --- 准确率的定义，其实就是计算 1 占整个样本的比率

# 设置

net = LR() # 类的实例化，创建一个实例
criterion = nn.CrossEntropyLoss() # 使用 CrossEntropyLoss 损失
optm = torch.optim.Adam(net.parameters()) # Adam 优化
epochs = 1000 # 训练 1000 次

# 开始训练

for i in range(epochs):
    # 指定模型为训练模式，计算梯度
    net.train()
    # 输入值都需要转换成 torch 的Tensor
    x = torch.from_numpy(train_data).float()
    y = torch.from_numpy(train_lab).long()
    y_hat = net(x)
    loss = criterion(y_hat, y) # 计算损失
    optm.zero_grad() # 前一步的损失清零
    loss.backward() # 反向传播
    optm.step() # 优化
    if (i + 1) % 100  == 0:  # 这里我们每 100 次输出相关的信息
        # 指定模型为计算模式
        net.eval()
        test_in = torch.from_numpy(test_data).float()
        test_l = torch.from_numpy(test_lab).float()
        test_out = net(test_in)
        # 使用我们的测试函数计算准确率
        accu = test(test_out, test_l)
        print("Epoch:{}, Loss:{:.4f}, Accurary:{:.2f}".format(i+1, loss.item(),accu))

准确率：