高斯滤波与双边滤波原理、MATLAB实现及结果对照
本文详细介绍高斯滤波和双边滤波的原理并给出MATLAB实现，最后对照高斯滤波与双边滤波的效果。
目录
一、滤波原理
1.1 一维高斯分布
1.2 二维高斯分布
1.3 高斯滤波总结
二、双边滤波
1. 双边滤波的原理
2. 双边滤波是如何实现“保边去噪”的？
3. MATLAB实现双边滤波
4. 关于sigma值的选取
4.1 空间域sigma 选取
4.2 值域sigma 选取
三、双边滤波与高斯滤波结果对照
3.1 仿真图像对照
3.2 真实图像对照
3.3 总结
一、滤波原理
参考：https://blog.csdn.net/nima1994/article/details/79776802（高斯滤波的原理）
划重点：
空域滤波的本质即在窗口内“取平均”，模板半径越大，模糊效果越强。
高斯滤波中，高斯函数是用来计算模板权重的，其依据为：连续图像中，越靠近的点关系越密切，越远离的点关系越疏远，因此，加权平均更合理，即距离中心点越近的点权重越大，距离越远的点权重越小。
1.1 一维高斯分布
而一维高斯分布（正态分布）刚好满足这一条件，如图1.
图1 正态分布“钟形曲线”
一维高斯分布公式见式（1），其中均值
决定了曲线的中心点，
决定了曲线的宽度，越大曲线越宽。
…………（1）
MATLAB实现一维高斯函数：
function g = Gaussian(X,avg,sigma)
%% 功能说明：一维高斯分布
%% 参数说明：avg -- 均值,决定中心点位置
% sigma -- 标准差，决定曲线宽度
temp_1 = 1 / (sigma * sqrt(2*pi));
temp_2 = -(X - avg).^2./(2*sigma^2);
g = temp_1 * exp(temp_2);
g = g ./ sum(g(:));
end
使用上述功能绘制不同值对应的曲线，代码如下：
X = -15:0.1:15;
avg = 0; % 图像中心点为0
sigmas = [1;2;3;4];
for i = 1:length(sigmas)
g = Gaussian(X,avg,sigmas(i));
plot(X,g)
hold on
end
legend('\sigma = 1','\sigma = 2','\sigma = 3','\sigma = 4');图像如图2，显然，决定了曲线的宽度，越大曲线越宽，且图像关于x = avg（这里为0）对称。
图2 不同值对应的一维高斯分布
补充说明：之前做了min-max标准化，将不同sigma值对应的曲线的取值范围均映射在了[0,1]范围内，但现在发现这种做法忽略了sigma取值对曲线高度的影响。
（高斯分布的性质：曲线下方与x轴上方的面积之和为1）sigma的取值不仅决定了曲线的宽度，也决定了曲线的高度，sigma越大，曲线越宽越矮；sigma越小，曲线越窄越高。
1.2 二维高斯分布
将x = x,y分别代入公式（1）后，二者相乘即可得到二维高斯分布公式（2）：
…………（2）
这里令
可得简化版二维高斯分布函数公式（3）：
…………（3）
根据公式（3）即可计算高斯滤波模板中每个点的权重。
二维高斯函数，代码如下：
function [G] = Gaussian(R,sigma)
%% 功能说明：二维高斯函数，可用于计算高斯滤波权重矩阵
% 高斯滤波：仅考虑了空域信息，未考虑灰度相似性
%% 输入参数：R -- 模板半径
% sigma -- 标准差
[X,Y] = meshgrid(-R:0.1:R);
temp1 = 1/(2*pi*sigma^2);
temp2 = -(X.^2 + Y.^2)/(2*sigma^2);
G = temp1 * exp(temp2);
G = G./sum(G(:)); % 模板的权重之和必须等于1。
% 绘制模板图
figure
surf(X,Y,G);
shading interp;
end大小为15*15，标准差为2的二维高斯分布模板如图3所示
图3 大小为11*11的二维高斯分布
使用大小为5*5，标准差为0.3的模板对含有弱小目标和云层的图像进行高斯模糊，如图4所示。
图4 大小为5*5，标准差为0.3的模板高斯模糊滤波结果
1.3 高斯滤波总结
高斯滤波只考虑了图像像素之间的空间相似性，即连续图像中，越靠近的点关系越密切，越远离的点关系越疏远。
二、双边滤波
1. 双边滤波的原理
参考：https://blog.csdn.net/Chaolei3/article/details/88579377
双边滤波是一种非线性的方法，与高斯滤波相比，双边滤波不仅考虑了图像的空间相似性，也考虑了其灰度相似性，可以达到“保边去噪”的目的。
双边滤波包含两部分：空域矩阵与值域矩阵，空域矩阵可类比高斯滤波，用于模糊去噪；值域矩阵根据灰度相似性得到，用来保护边缘。
空域矩阵计算公式（4），值域矩阵计算公式（5）
…………（4）
…………（5）
公式说明：定义(i, j)为中心点坐标，(k, l)为以点(i, j)为中心的邻域内任意一点。
公式（4）（5）相乘即为双边滤波权重矩阵计算公式（6）
…………（6）
最后，计算加权平均值作为中心点坐标滤波后的值
………… （7）
2. 双边滤波是如何实现“保边去噪”的？
参考：https://blog.csdn.net/Jfuck/article/details/8932978?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2.control
由公式（4），空间域权重矩阵的权重分布仍然是“钟形”，即距中心点越近，所占权重越大；
由公式（5）（6），已知
是过（0，1）点的减函数，即灰度差值越大，权重越小，平滑效果越差，反之，灰度差值越小，权重越大，平滑效果越好。所以，当中心点位于边缘处时，灰度差值大，空间域平滑效果削弱，边缘被保留；当邻域灰度值接近中心点时，灰度差值接近0，值域权重接近1，此时滤波效果取决于空间域权重矩阵，与高斯滤波效果一致。
公式（7）的含义：滤波后中心点的值 = 权重矩阵 .* 原始图像 （且保证权重之和为1，归一化处理）（参照滤波原理）
图5 双边滤波“保边去噪”原理图
3. MATLAB实现双边滤波
function b = BF_Filter(img,r,sigma_d,sigma_r)
%% 功能说明：双边滤波，用于计算双边滤波后的图像
% 双边滤波是一种非线性方法，同时考虑图像的空域信息和灰度相似性。
% 通过空域矩阵和值域矩阵形成新的权重矩阵，其中，空域矩阵用来模糊去噪，值域矩阵用来保护边缘。
%% 输入参数：img -- 待滤波图像
% r -- 模板半径，e.g. 3*3模版的半径为1
% sigma_d -- 空域矩阵标准差
% sigma_r -- 值域矩阵标准差
% 判断是否为灰度图像
if(size(img,3)>1)
img = rgb2gray(img);
end
[x,y] = meshgrid(-r:r);
% 空域权重矩阵 size = (2r+1)*(2r+1)
w_spacial = exp(-(x.^2 + y.^2)/(2*sigma_d.^2));
[m,n] = size(img);
img = double(img);
% 扩展图像，size = (m+2r)*(n+2r)
f_temp = padarray(img,[r r],'symmetric');
% 滑动窗口并滤波
b = zeros(m,n); % 滤波后图像
for i = r+1:m+r
for j = r+1:n+r
temp = f_temp(i-r:i+r,j-r:j+r);
w_value = exp(-(temp - img(i-r,j-r)).^2/(2*sigma_r^2)); % size = (2r+1)*(2r+1)
w = w_spacial .* w_value;
s = temp.*w;
b(i-r,j-r) = sum(s(:))/sum(w(:));
end
end
end4. 关于sigma值的选取
参考：https://blog.csdn.net/Jfuck/article/details/8932978?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-2.control
4.1 空间域sigma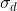 
选取
核大小通常为，即
因为距离中心点大小之外的系数与中点的系数值比较小，可以认为此之外的点与中心点几乎没有联系，权重系数可看作0.
4.2 值域sigma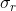 
选取
图6 
图像
当
，灰度差值范围为[0,255]时，x 的取值范围 
，值域范围为：[0.3679,1];
当
，灰度差值范围为[0,255]时，x 的取值范围 
，值域范围为：[0.01832,1];
所以，sigma越大，权重值域范围越小，此时即使邻域灰度值与中心点灰度值之差较大，其对应权重也会很大，这与双边滤波“保边”的初衷相违背；sigma越小，权重值域范围越大，此时当邻域灰度值域中心点灰度值之差较大时，其对应权重越小，可以削弱“平滑”，达到“保边”效果。
综上，sigma越大，边缘越模糊，sigma-->∞时，x-->0，权重-->1，与高斯模板相乘后可认为等效于高斯滤波；
sigma越小，边缘越清晰，sigma-->0时，x-->∞，权重-->0，与高斯模板相乘后可认为系数皆相等，等效于源图像。
三、双边滤波与高斯滤波结果对照
3.1 仿真图像对照
生成含明显边缘的图像，如图7所示。
图7 仿真图像
img_B = zeros(250,250);
img_B(:,40:50) = 1;
img_B(:,180:200) = 1;
img_B(100:105,:) = 1;
imshow(img_B)高斯滤波与双边滤波结果如图8所示，显然，双边滤波可以更好地保留图像的边缘信息。
图8 双边滤波与高斯滤波仿真图像对比结果
%% 高斯滤波
r = 7;
sigma_d = 1;
G = Gaussian(r, sigma_d);
g = imfilter(img_B, G, 'symmetric');
%% 双边滤波
sigma_r = 3;
b = BF_Filter(img_B,r,sigma_d,sigma_r);
figure
subplot(1,2,1)
imshow(b);title([num2str(2*r+1),'*',num2str(2*r+1),'双边滤波结果','\sigma_d=1 ,',' \sigma_r=3']);
subplot(1,2,2)
imshow(g);title([num2str(2*r+1),'*',num2str(2*r+1),'高斯滤波结果','\sigma_d=1']);3.2 真实图像对照
从结果来看，对于含有云层等结构背景及弱小目标的图像，与高斯滤波相比，双边滤波可以很好地保留图像的边缘（结构）信息。
图9 原真实图像
图10 双边滤波与高斯滤波真实图像对比结果
img = imread('cloud.bmp');
if(size(img,3)>1)
img = rgb2gray(img);
end
r = 7;
sigma_d = 0.5;
G = Gaussian(r, sigma_d);
img_g = imfilter(img, G, 'symmetric');
sigma_r = 3;
img_b = BF_Filter(img,r,sigma_d,sigma_r);
subplot(1,3,1);
imshow(img);title('原图');
subplot(1,3,2)
imshow(img_g,[]);title('高斯滤波结果');
subplot(1,3,3);
imshow(img_b,[]);title('双边滤波结果');3.3 总结
结合弱小目标检测的课题目标，双边滤波适合预测含有丰富边缘（结构）信息的背景预测，通过实验选择合适的sigma值，对背景进行预测，原图-预测背景图=目标图（STI），然后从STI图中检测目标，下一步需要进行深入探究。