《PyTorch深度学习实践》完结合集 · Hongpu Liu · overview（1）

目录

前言

一、Pytorch 的安装

二、线性模型（穷举法）

三、梯度下降算法实现

四、反向传播

结语

---

前言

 刘老师的课件讲的挺好的！！！我是结合着吴恩达深度学习的课程一起来看的！！！

刘老师的课讲的很生动！！！里面有代码的详解也有理论推导，适合初学者！！！

 课程链接：《PyTorch深度学习实践》完结合集https://www.bilibili.com/video/BV1Y7411d7Ys?p=1

一、Pytorch 的安装

详解：Pytorch(一) Pytorch 的安装：https://blog.csdn.net/qq_23013309/article/details/103965619

二、线性模型（穷举法）

#! /usr/bin/env python
# -*- coding: utf-8 -*-

'''
时间：2021.8.12
作者：手可摘星辰不去高声语
文件名：02-线性模型1.py
功能：穷举法实现第一种（ y = w * x ）线性模型
'''


import numpy as np
import matplotlib.pyplot as plt


# 准备训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]


# 第一种（ y = w * x ）线性模型
def forward(x):
    return x * w


# 计算损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y)**2


if __name__ == '__main__':
    w_list = []
    mse_list = []
    # 计算数据组数
    numb_train = len(x_data)
    # 提前获取到条件：w权值的范围大致处于0~4,遍历每一个w
    for w in np.arange(0.0, 4.1, 0.1):
        sum_loss_val = 0
        count = 0
        w_list.append(w)
        # 遍历计算每一个w下的每一个（x，y）的loss
        for x_val, y_val in zip(x_data, y_data):
            count = count % numb_train+ 1
            y_val_pred = forward(x_val)
            loss_val = loss(x_val, y_val)
            sum_loss_val = sum_loss_val + loss_val
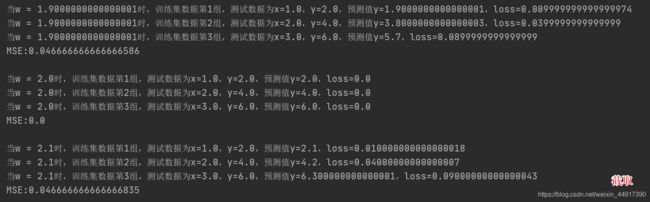
            print("当w = {}时，训练集数据第{}组，测试数据为x={}，y={}，预测值y={}，loss={}"
                  .format(w, count, x_val, y_val, y_val_pred, loss_val))
        # 每一个w结束后，需要计算每组loss的平均值，即MSE
        mse = sum_loss_val/numb_train
        mse_list.append(mse)
        print("MSE:{}\n".format(mse))

    # 绘制二维图像（mse随w变化）
    plt.plot(w_list, mse_list)
    plt.xlabel("w")
    plt.ylabel("mse")
    plt.title("Linear Model : y = w * x ")
    plt.show()

 

作业：

#! /usr/bin/env python
# -*- coding: utf-8 -*-

'''
时间：2021.8.13
作者：手可摘星辰不去高声语
文件名：03-线性模型2.py
功能：穷举法实现第二种（ y = w * x + b ）线性模型
'''


import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter


# mpl模块载入的时候加载配置信息存储在rcParams变量中，rc_params_from_file()函数从文件加载配置信息
mpl.rcParams['legend.fontsize'] = 20
font = {
    'color': 'b',
    'style': 'oblique',
    'size': 20,
    'weight': 'bold'
}
fig = plt.figure(figsize=(10, 8))  # 参数为图片大小
ax = fig.gca(projection='3d')  # get current axes，且坐标轴是3d的
ax.set_aspect('equal')  # 坐标轴间比例一致

# 准备训练集
x_data = [0.9, 1.8, 4.1]
y_data = [2.9, 6.1, 9.2]


# 第一种（ y = w * x ）线性模型
def forward(x, w, b):
    return x * w + b


# 计算损失函数
def loss(x, y, w, b):
    y_pred = forward(x, w, b)
    return (y_pred - y)**2


if __name__ == '__main__':
    w_train_start, w_train_end, w_train_step = -1, 5, 0.1
    b_train_start, b_train_end, b_train_step = -2.0, 5.0, 0.1
    w_list = []
    b_list = []
    mse_array = []
    count_num = 0
    # 计算数据组数
    numb_train = len(x_data)
    # 提前获取到条件：w权值的范围大致处于0~4,遍历每一个w
    # 提前获取到条件：b的范围大致处于-2~2,遍历每一个b
    for w_train in np.arange(w_train_start, w_train_end, w_train_step):
        count = 0
        mse_list = []
        w_list.append(w_train)

        for b_train in np.arange(b_train_start, b_train_end, b_train_step):
            # 只加入一组b_train到b_list当中去即可
            if count_num == 0:
                b_list.append(b_train)
            sum_loss_val = 0

            # 遍历计算每一个(w,b)下的每一个（x，y）的loss
            for x_val, y_val in zip(x_data, y_data):
                count = count % numb_train + 1
                y_val_pred = forward(x_val, w_train, b_train)
                loss_val = loss(x_val, y_val, w_train, b_train)
                sum_loss_val = sum_loss_val + loss_val
                print("当(w,b) = ({},{})时，训练集数据第{}组，测试数据为x={}，y={}，预测值y={}，loss={}"
                      .format(w_train, b_train, count, x_val, y_val, y_val_pred, loss_val))

            # 每一个(w,b)结束后，需要计算每组loss的平均值，即MSE
            mse = sum_loss_val/numb_train
            print("MSE:{}\n".format(mse))
            mse_list.append(mse)
        mse_array.append(mse_list)
        count_num = count_num + 1

    # 绘制三维图像（mse随w，b变化）
    # 准备数据

    x = np.array(b_list)
    y = np.array(w_list)
    # 格点矩阵,原来的x行向量向下复制len(y)次，形成len(y)*len(x)的矩阵，即为新的x矩阵；
    # 原来的y列向量向右复制len(x)次，形成len(y)*len(x)的矩阵，即为新的y矩阵；
    # 新的x矩阵和新的y矩阵shape相同
    x, y = np.meshgrid(x, y)
    z = np.array(mse_array)
    surf = ax.plot_surface(x, y, z, cmap="rainbow")

    # 自定义z轴
    ax.set_zlim(-5, 100)
    ax.zaxis.set_major_locator(LinearLocator(10))  # z轴网格线的疏密，刻度的疏密，20表示刻度的个数
    ax.zaxis.set_major_formatter(FormatStrFormatter('%.01f'))  # 将z的value字符串转为float，保留1位小数

    # 设置坐标轴的label和标题
    ax.set_xlabel('b', size=15)
    ax.set_ylabel('w', size=15)
    ax.set_zlabel('loss', size=15)
    ax.set_title("Surface plot", weight='bold', size=20)

    # 添加右侧的色卡条
    fig.colorbar(surf, shrink=0.6, aspect=8)  # shrink表示整体收缩比例，aspect仅对bar的宽度有影响，aspect值越大，bar越窄
    plt.show()

 

三、梯度下降算法实现

  

 

 

  

 

#! /usr/bin/env python
# -*- coding: utf-8 -*-

'''
============================================
时间：2021.8.13
作者：手可摘星辰不去高声语
文件名：04-梯度下降法.py
功能：
1、Ctrl + Enter      在下方新建行但不移动光标；
2、Shift + Enter     在下方新建行并移到新行行首；
3、Shift + Enter     任意位置换行
4、Ctrl + D          向下复制当前行
5、Ctrl + Y 　　      删除当前行
6、Ctrl + Shift + V  打开剪切板
7、Ctrl + /          注释(取消注释)选择的行；
8、Ctrl + E 　　　  　可打开最近访问过的文件
9、Double Shift + /  万能搜索
============================================
'''


import matplotlib.pyplot as plt


# 准备训练集
x_data = [0.9, 1.8, 4.1]
y_data = [2.9, 6.1, 9.2]


def forward(x, w):
    return x * w


# 计算代价函数
def cost(x_train_data, y_train_data, w_train):
    cost_val = 0
    for x, y in zip(x_train_data, y_train_data):
        y_pred = forward(x, w_train)
        cost_val = cost_val + (y_pred - y)**2
    return cost_val/len(x_data)


def gradient(x_train_data, y_train_data, w_train):
    grad = 0
    for x, y in zip(x_train_data, y_train_data):
        grad = grad + 2 * x * (w_train * x - y)
    return grad / len(x_data)


if __name__ == '__main__':
    loss_list = []
    epoch_list = []
    w = 10
    rate = 0.01
    for epoch in range(100):
        mse = cost(x_data, y_data, w)
        grad_val = gradient(x_data, y_data, w)
        w = w - rate * grad_val
        epoch_list.append(epoch)
        loss_list.append(mse)
        print("Epoch:{}\t w={}\t loss={}".format(epoch, w, mse))

    plt.plot(epoch_list, loss_list)
    plt.xlabel("Epoch")
    plt.ylabel("MSE")
    plt.grid()
    plt.show()

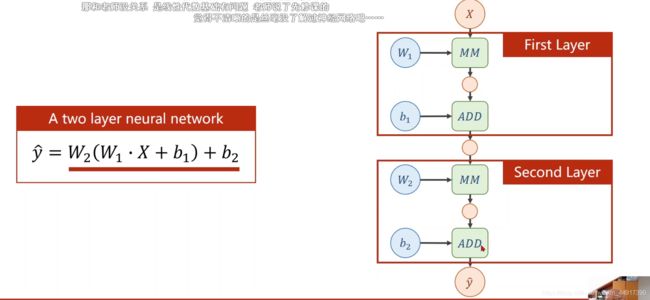
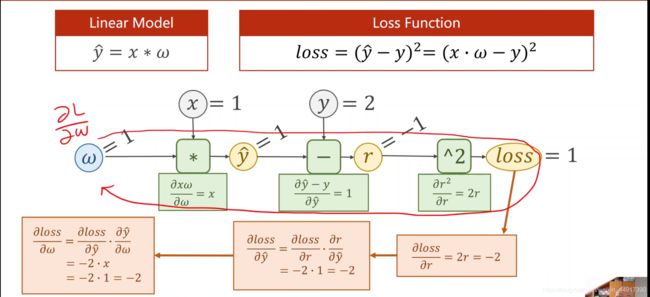
四、反向传播

 

 

 

 

结语

如果上面的代码有写错的地方，欢迎大家批评指正！！！