异常检测方法在时间序列数据上的应用综述（记录）

介绍

1. 异常值的定义：

   “An observation which deviates so much from other observations as to arouse suspicions that it was generated by a different mechanism.
   一个与其他观察值偏离非常大，以至于让人怀疑它是用另一种不同的机制中产生的数据。

2. 异常值的两种不同用途
   

   • 正常数据中的异常点，可以理解为数据噪声，是模型训练中希望剔除的数据，它的存在会减低数据的质量，影响模型的训练效果
   • 数据中的异常值，是在训练中希望能够检测和分析的数据，它反映出了系统中某些不正常现象或者变化的发生，是希望能够找到并用来作为训练数据的样本。

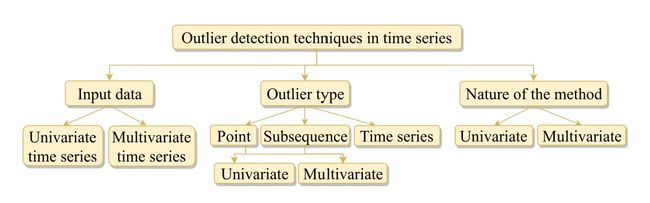
时间序列异常值检测的分类

1. 输入数据的类型

   • 一维数据
   • 多维数据

2. 异常值的类型

   • 异常点
     异常值是样本中一个点
     
   • 异常子序列
     异常值是多个连续样本组成的一个序列
     
   • 异常时间序列
     异常值是由某个变量的时间序列整体组成，只能用于多维输入的情况
     

3. 检测方法的原理

   • 以单变量数据作为输入
     也可以用域多变量数据的处理，不考虑多变量之间的相关关系
   • 以多变量数据作为输入

4. 注意
   由于异常值的定义一般取决于选择的方法，或者数据本身的特点，因此当选择整个时间序列作为分析对象时，得到的异常点是全局的(global)，而仅选择一个邻域或者一段子序列进行分析的时候，得到的异常点是局部的(local)
   一个在全局看正常的样本，在局部邻域内可能是异常的点

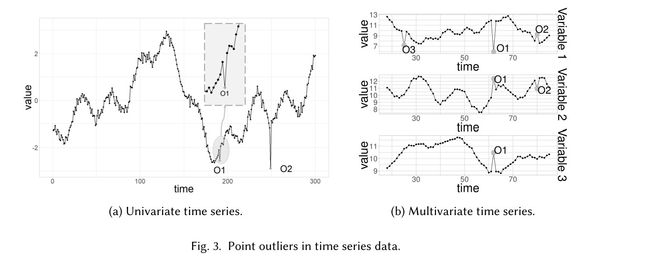
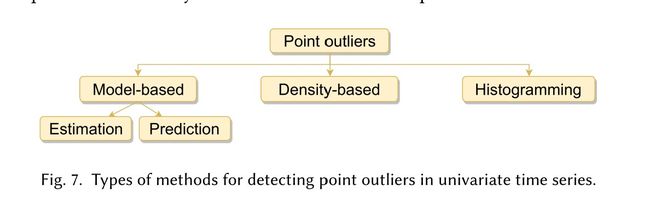
点异常样本的检测

两大主要特点：

1. 是否将时间作为变量

   • 完全考虑样本的时间顺序
   • 将样本划分为不同的时间窗，在一个时间窗内，不区分时间顺序
   • 不考虑样本的时间顺序

2. 是否能实现实时预测

   • 一些异常值检测算法，需要同时考虑一个点过去和将来的数据，不能实现来一个新样本，判断一个
   • 另一些检测算法，则只考虑新样本点和之前的历史数据，可以实现实时判断样本点是否是异常点

单变量时间序列

主要分类：

基于模型的方法

通过判断样本值与期望值之间的差距是否超过临界值，来判断样本点是否是异常样本

$$\left|x_t-{\hat{x}}_t\right|>\tau$$

按照求期望值的不同，又可分为：
$$\begin{array}{lccccc}& \text{ Data used }& ⟶& \text{ Expected value }& ⟶& \text{ Point outliers }\\ \text{ Estimation models }& \left\{x_{t-k_1},\dots ,x_t,\dots ,x_{t+k_2}\right\}& ⟶& {\hat{x}}_t& ⟶& \left|x_t-{\hat{x}}_t\right|>\tau \\ \text{ Prediction models }& \left\{x_{t-k},\dots ,x_{t-1}\right\}& ⟶& {\hat{x}}_t& & \end{array}$$

基于预测模型

​ 基于预测模型的方法，仅使用过去的数据来预测新样本的预测值

常见的预测模型

1. 固定模型

DeepAnT

2. 变化模型

ARIMA

3. 极值理论

   SPOT（Peaks-Over_threshold）固定分布

   DSPOT 漂移分布

基于估计模型

​ 依据估计模型的方法，同时使用过去和将来的数据，预测某样本的预测值

常见的估计模型：

1. 基于常数或分段统计特征

   MAD（Median Absolute Deviation ）

2. 基于拟合模型和变量分布函数

   Extreme Studentized Deviate (ESD)

3. 基于残差

   ARIMA （Autoregressive Integrated Moving Average mode）

基于密度的方法

$$x_t\text{ is an outlier }⟺\left|\left\{x\in X\mid d\left(x,x_t\right)\le R\right\}\right|<\tau$$

$${\tau }_p+{\tau }_s<\tau$$

${\tau }_p$ 和 ${\tau }_s$ 分别是一个点之前和之后，距离小于R的点的数量

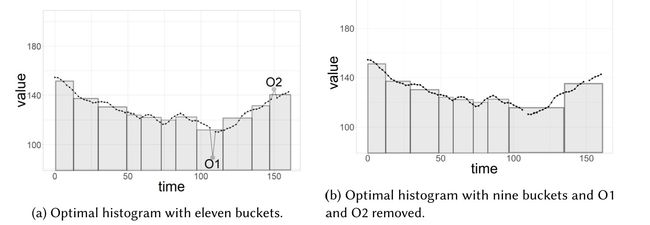
基于直方图的方法

通过定义一个异常评价函数（越低越好），当除去一个点后，若评价值降低，则将此点视为异常值

多变量时间序列

单变量方法

事实上，当不考虑多变量之间的相关性时，所有上面提到的单变量方法，都可以用于多变量时间序列异常检测，当然实际使用中，这样的做法很少见

1. 对每个维度分别进行异常值检测

   Long Short-Term Memory (LSTM)

2. 数据降维

   将相关的多维变量，降维成不相关的多维变量

   常见的降维方法：

   • 增量主成分分析
   • 最优投影法
   • Independent Component Analysis (ICA)

3. 数据转换

   将多变量数据转换成一维的时间序列数据

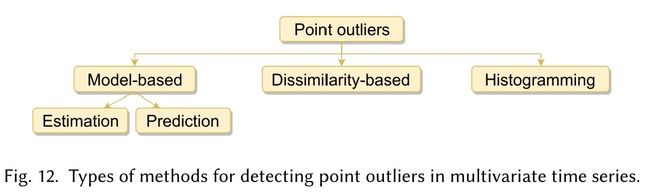
多变量方法

1. 基于估计模型
   $$\Vert x_t-{\hat{x}}_t\Vert >\tau$$

   • autoencoders

2. 基于预测模型

   • Contextual Hidden Markov Model (CHMM)
   • DeepAnt

3. 基于相异度

   不训练模型，而直接比较样本之间相似度

4. 基于直方图

   方法类似上面的单变量方法中的介绍

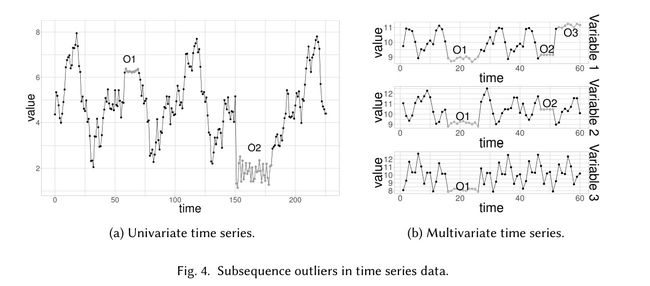
序列异常段的检测

这里的定义的异常不再是某一时刻的单一样本点，而是一段时间内连续的样本点构成的序列，它们的某些特征与正常变化不同

通常的分类有以下几种

1. 考虑子序列的长度

   按照不同方法在长度选择上的不同，又可分为：

   • 固定长度检测（需要手动设置检测片段的长度）
   • 可变长度检测

2. 考虑系列的表达方式

   由于考虑原始的时间序列数据，通常会导致问题过于复杂，因此通常会使用离散化（Discretization）处理的方法，对原始数据进行处理

   • equal-frequency binning
   • equal-width binning

3. 考虑周期性

   有的场景下，时间序列数据会随着周期性不断地重复，因此在进行异常检测时，除了时间之外，还需要额外考虑周期性的影响

按照对流数据处理方式不同又可分为以下几类：

1. 来一个新点，就判断包含此点的序列是否是异常序列
2. 来一段序列，判断此序列是否异常
3. 来一批数据，判断数据中是否存在异常序列

单变量时间序列

1. 不协调检测

   将一段序列与其他的序列段进行比较，找到与其他序列差异最大的序列段

   
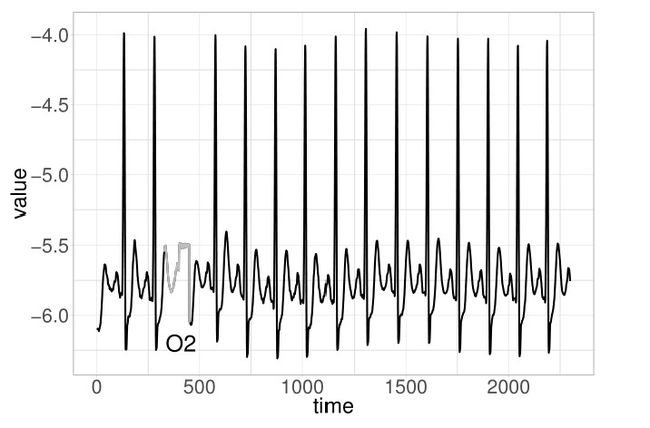
   • 使用HOT-SAX方法的各种变体，来降低比较过程中的时间复杂度

   特点：往往需要用户来指定检测的时间长度，并且输出结果不能判断这个点是异常点，而通常需要人工来判断，因为它只是检测出最不寻常的点，不代表这个点就是异常点，通常也不没有一个特定的判断临界值等

2. 相异度检测
   $$s(S,\hat{S})>\tau$$

s()函数是衡量两段子序列之间相异度的函数，当相异度超过一个临界值，被标记为异常点

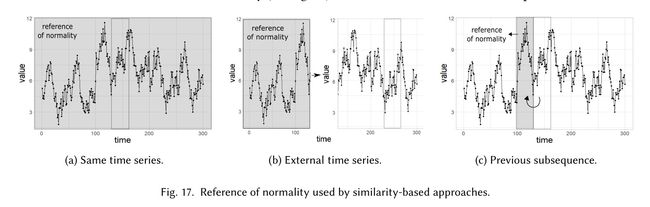
按照衡量相异度时，选择作为正常值的参考不同，又可分为以下几种方法：

• 以相同时间序列内容作为参考

  • 聚类方法

    （通常需要对原始的连续数据进行离散化处理）通过将不同的子序列进行聚类，将聚类中心作为期望值，从而将远离中心，或者所在类成员比较少的，判断为异常序列

    • Fuzzy C-Means (FCM)
    • 动态聚类

  • 相异度衡量

• 使用外部序列作为参考

• 使用历史序列作为参考

3. 基于预测模型

$$\sum _{i=p}^{p+n-1}\left|x_i-{\hat{x}}_i\right|>\tau$$

$$\sum _{i=p}^{p+n-1}\left|x_i-{\hat{x}}_i\right|>\tau$$

• 预测每个序列点（上面的单点预测方法都可以用）
• 预测整段时间序列（通常使用CNN）

4. 基于频率
   $$|f(S)-\hat{f}(S)|>\tau$$

通过预计频率与真实频率的差异，来判断是否是异常序列

4. 基于信息理论
   $$I(S)\times f(S)>\tau$$

I(s)是序列携带的信息，序列越罕见，信息值越大

f(s)是序列出现的此时

多变量时间序列

基于单变量检测方法

通过不考虑多维数据之间的相关性，或者将多维相关数据降维成低维不相关的数据，从而使用上面单变量的检测方法进行检测

基于多变量检测的方法

• 估计模型
• 预测模型
• 异常度方法

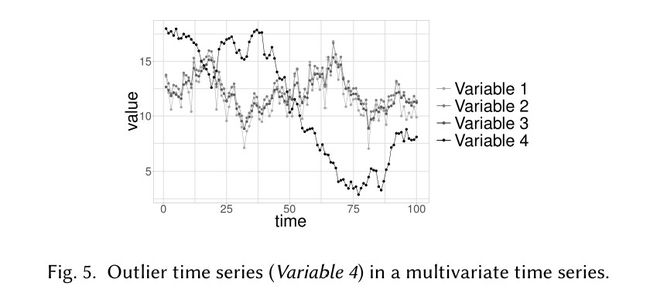
异常时间序列的检测

异常时间序列是指多变量时间序列中，某个或多个变量的全部数据出现异常

降维方法

略

异常度评价

略

未来研究方向

1. 目前的大部分研究，在判断异常值是否是临界值时，通常都使用的是，手动设置threshold的方法，几乎没有研究使用的是动态的threshold
2. 大部分研究，都假设采集到的数据，是按照一定时间间隔，规律采集，这与部分实际情况不太符合
3. 部分研究的检测模型都不考虑时间变量，这在今后的研究中可能会有改变
4. 很少有研究关注实时检测的问题，没有讨论模型在实际情况下，能否实时地实现快速地检测
5. 目前还没有人研究在多变量时间序列中，如何检测周期性异常子序列
   指多变量时间序列中，某个或多个变量的全部数据出现异常

降维方法

略

异常度评价

略

未来研究方向

1. 目前的大部分研究，在判断异常值是否是临界值时，通常都使用的是，手动设置threshold的方法，几乎没有研究使用的是动态的threshold
2. 大部分研究，都假设采集到的数据，是按照一定时间间隔，规律采集，这与部分实际情况不太符合
3. 部分研究的检测模型都不考虑时间变量，这在今后的研究中可能会有改变
4. 很少有研究关注实时检测的问题，没有讨论模型在实际情况下，能否实时地实现快速地检测
5. 目前还没有人研究在多变量时间序列中，如何检测周期性异常子序列
6. 很少有研究关注异常的传递现象，比如一个变量突变后，经过一段时间传递到另一个变量上面