【Meta-Learning】Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
文章目录
- Abstract
- 1 Introduction
- 2 Model-Agnostic Meta-learning
-
- 2.1 Meta-Learning Problem Set-up
- 2.2 A Model-Agnostic Meta-Learning Algorithm
- 3 Experimental Evaluation
-
- 3.1 Regression
- 3.2 Classification
- 4 Discussion and Future Work
Abstract
- model-agnostic
提出一种模型未知的元学习方法,可以和任意采用梯度下降法进行训练的模型兼容,如分类、回归和强化学习。 - a small number of training samples
元学习目标是:用一系列不同的学习任务进行训练,得到的模型能够在仅存在少量训练样本的情况下,就足以用于解决新的学习任务。 - Easy to finetune
训练模型参数时仅仅需要少量的梯度更新就能得到较好的性能。
1 Introduction
- Key idea: 训练模型的初始参数,使得模型在一个新任务上应用时,只用通过一步或少数几步梯度更新就能具有最优效果。
最大化损失函数对参数的敏感度,使得参数微小的变化即可优化任务损失。 - 本文所提算法可用于不同的模型类型(全连接网络、卷积网络),不同的领域(few-shot回归、图像分类、强化学习)。
2 Model-Agnostic Meta-learning
2.1 Meta-Learning Problem Set-up
考虑用 f f f来表示一个模型,该模型能将observation x x x 映射到输出 a a a上。
在元学习中,每一个完整的任务被看成一个训练样本,训练所得模型的作用是要使其能够适用于其他新的任务。因此采用一个通用的表示方法来代表每个任务。
T = { L ( x 1 , a 1 , . . . , x H , a H ) , q ( x 1 ) , q ( x t + 1 ∣ x t , a t ) , H } T=\left\{L(x_1,a_1,...,x_H,a_H),q(x_1),q(x_{t+1}|x_t,a_t),H \right\} T={L(x1,a1,...,xH,aH),q(x1),q(xt+1∣xt,at),H}
L L L表示损失函数, q ( x 1 ) q(x_1) q(x1)是初始观察量的分布, q ( x t + 1 ∣ x t , a t ) q(x_{t+1}|x_t,a_t) q(xt+1∣xt,at)为过渡分布(transition distribution), H H H是片段长度(episode length)。在独立同分布问题中, H = 1 H=1 H=1。
考虑训练一个模型,可适用于服从分布 p ( T ) p(T) p(T)的任务集合。以K-shot learning为例,每个训练任务中仅有K个样本,从 p ( T ) p(T) p(T)中sample一个新任务 T i T_i Ti,模型在新任务的测试集上所得的损失 L T i L_{T_i} LTi即为元学习的损失。
2.2 A Model-Agnostic Meta-Learning Algorithm
本文通过元学习提出一种能够学习任何标准模型参数的方法,使模型能够快速适应新任务。其方法背后的intuition:网络中的某些中间特征表示比其他的更具有迁移性,可以广泛应用到服从分布 p ( T ) p(T) p(T)的所有任务上, 而不仅仅是一个单一的任务。
首先,将模型表示成一个参数化函数 f θ f_{\theta} fθ, θ \theta θ是模型的参数,当模型应用到一个新任务 T i T_i Ti上时,采用一步或多步梯度下降来更新模型参数:(以一次梯度更新为例)
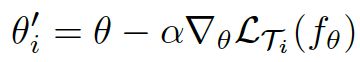
通过优化所有 f θ i ′ f_{\theta_i'} fθi′在其相应的任务 T i T_i Ti上的表现,来训练模型的初始参数 θ \theta θ,meta-objective表示如下:
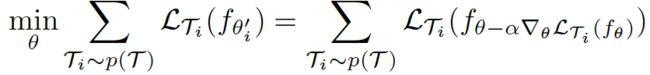
同样采用梯度下降法来更新 θ \theta θ:
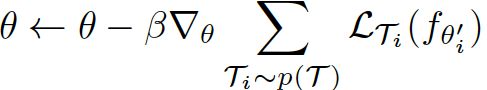
算法流程如下:
- 针对待解决的任务选择模型,并初始化模型参数 θ \theta θ
- 从分布 p ( T ) p(T) p(T)中采样一组训练任务 T i T_i Ti,对所有的任务进行以下步骤:
a. 计算任务 T i T_i Ti中 K K K个样本上的损失 ▽ θ L T i ( f θ ) \triangledown_\theta L_{T_i}(f_\theta) ▽θLTi(fθ)
b. 采用梯度下降算法更新模型参数
θ i ′ = θ − α ▽ θ L T i ( f θ ) \theta'_i =\theta -\alpha\triangledown_\theta L_{T_i}(f_\theta) θi′=θ−α▽θLTi(fθ)
最终目标是要找到一个最佳的模型初始参数 θ \theta θ,使得网络只需要进行少数更新就能在所有任务上都能达到最佳的效果。即找到一个 θ \theta θ使 ∑ T i ∼ p ( T ) L T i ( f θ i ′ ) \sum_{T_i\sim p(T)}L_{T_i}(f_{\theta'_i}) ∑Ti∼p(T)LTi(fθi′)最小。- 采用梯度下降算法优化初始参数 θ \theta θ:
θ ← θ − β ▽ θ ∑ T i ∼ p ( T ) L T i ( f θ i ′ ) \theta\leftarrow\theta-\beta \triangledown_\theta\sum_{T_i\sim p(T)}L_{T_i}(f_{\theta'_i}) θ←θ−β▽θ∑Ti∼p(T)LTi(fθi′)
至此,得到最终的最优初始参数 θ \theta θ。
3 Experimental Evaluation
实验待验证的问题有三点:
- Can MAMAL enable fast learning of new tasks?
MAML是否能够快速学习新任务? - Can MAML be used for meta-learning in multiple different domains, including supervised regression, classification, and reinforcement learning?
MAMAL是否能用于多个不同的领域,如有监督回归、分类及强化学习? - Can a model learned with MAML continue to improve with additional gradient updateds and/or examples?
采用MAML学习到的模型是否能够通过额外的梯度更新得以继续提升性能?
文章针对回归、分类和强化学习三类问题都分别进行了实验,(表明MAML适用于各个领域),这里只针对回归和分类问题进行整理。
3.1 Regression
待解决任务:通过一系列数据点来拟合一条正弦曲线,即给定 { ( x i , y i ) } i = 1 , . . . , K {\left\{(x_i,y_i) \right\}}_{i=1,...,K} {(xi,yi)}i=1,...,K,来预测正弦函数的幅值 A A A和相角 ϕ \phi ϕ,其中 A ∈ [ 0.1 , 5.0 ] , ϕ ∈ [ 0 , π ] , x i ∈ [ − 5.0 , 5.0 ] A\in[0.1,5.0],\phi\in[0,\pi],x_i\in[-5.0,5.0] A∈[0.1,5.0],ϕ∈[0,π],xi∈[−5.0,5.0]。

上图实验结果表明:
- 当数据点只有5个时,MAML仍然能够达到较好的拟合效果,而pre-training则无法在不过度拟合的情况下保证充分适应如此少的点。
- 同时,当数据点全都分布在曲线的其中一个半边时,MAML仍然能够较好的拟合另一个半边,说明MAML训练出的模型学到了正弦曲线的周期性本质。

上图实验结果表明:
MAML在一次梯度更新后就能大幅度提升模型准确率,并且继续进行提取更新时准确率能在一定范围内继续得以提升,而不会产生过拟合现象。
3.2 Classification
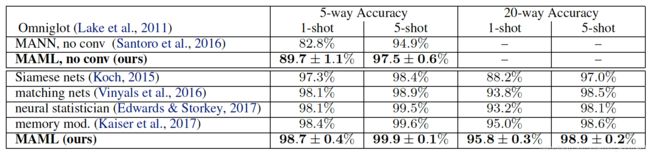
在数据集Omniglot和MiniImagenet上进行N-way K-shot的实验(K=1 or 5),实验结果如下:
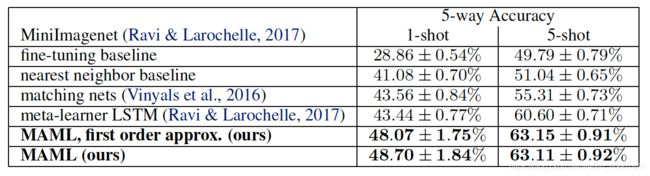
4 Discussion and Future Work
本文提出一种利用梯度下降来学习具备easily adaptable的模型参数的方法,其优势如下:
1)流程简单,且不引入额外需要学习的参数;
2)可以适用于任意能够采用梯度下降来训练的模型;
3)由于本方法仅产生一组初始权重,因此adaptation的过程可以通过任意数量的数据、任意次数的梯度更新来实现。