GNN,GCN学习整理

GNN

GNN定义

GNN是Graph Neural Network的简称，是用于学习包含大量连接的图的联结主义模型。当信息在图的节点之间传播时GNN会捕捉到图的独立性。与标准神经网络不同的是，GNN会保持一种状态，这个状态可以代表来源于人为指定的深度上的信息。

图神经网络处理的数据就是图，而图是一种非欧几里得数据。GNN的目标是学习到每个节点的邻居的状态嵌入，这个状态嵌入是向量且可以用来产生输出，例如节点的标记。如下图，最终的目的就是学习到红框的H，由于H是定点，因此可以不断迭代直到H的值不再改变即停止。

GNN来源

1. CNN：CNN可以提取大量本地紧密特征并组合为高阶特征，但CNN只能够操作欧几里得数据。CNN的关键在于局部连接、权值共享、多层使用；

2. graph embedding：在低维向量上学习表示图节点、边或者子图。思想源于特征学习和单词嵌入，第一个图嵌入学习方法是DeepWalk，它把节点看做单词并在图上随机游走，并且在它们上面使用SkipGram模型；

基于以上两种思想，GNN会在图结构上聚合信息，因此可以对输入/输出的元素及元素间的独立性进行建模。GNN还可以同时使用RNN核对图上的扩散过程进行建模。

GNN优点

1. 标准神经网络（CNN、RNN）无法解决图输入无序性，因为它们将点的特征看做是特定的输入；

2. 两点之间的边代表着独立信息，在标准神经网络中，这种信息被看做是点的信息，而GNN可以通过图结构来进行传播，而不是将其看做是特征；通常而言，GNN更新隐藏节点的状态，是通过近邻节点的权值和；

3. 高级人工只能需要更高的可解释性；标准神经网络可以生成合成图像或文档，但无法生成图；GNN可以生成无结构的数据（多种应用：文字分类、神经机器翻译、关系提取、图像分类）

GNN缺点

1. 更新节点的隐藏状态是低效的；

2. 在迭代中使用相同的参数，更新节点隐藏状态是时序的；

3. 在边上有一些信息化的特征无法在原始GNN中建模；如何学习边的隐藏状态也是问题；

4. 如果我们的目标是节点的表示而不是图，使用固定点H是不合适的

GCN

基础概念

图卷积神经网络(Graph Convolutional Network, GCN)是一类采用图卷积的神经网络，发展到现在已经有基于最简单的图卷积改进的无数版本，在图网络领域的地位正如同卷积操作在图像处理里的地位。

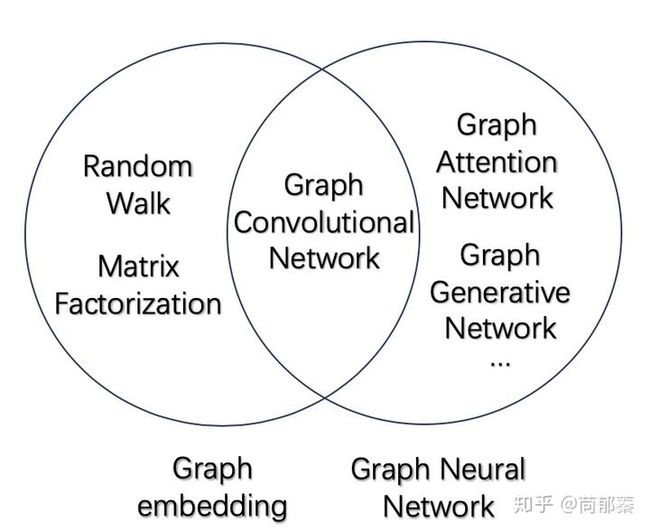
如上图所示，图卷积神经网络GCN属于图神经网络GNN的一类，是采用卷积操作的图神经网络，可以应用于图嵌入GE。

GCN理解

假设有一批图数据，其中有N个节点（node），每个节点都有自己的特征，设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，也称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。

GCN也是一个神经网络层，它的层与层之间的传播方式是：

这个公式中：

· A波浪=A+I，I是单位矩阵
· D波浪是A波浪的度矩阵（degree matrix），公式为
· H是每一层的特征，对于输入层的话，H就是X
· σ是非线性激活函数

这个部分，是可以事先算好的，因为D波浪由A计算而来，而A是我们的输入之一。

为了直观理解，使用论文中的一幅图：

上图中的GCN输入一个图，通过若干层GCN每个node的特征从X变成了Z，但是，无论中间有多少层，node之间的连接关系，即A，都是共享的。

假设构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式为：

最后，针对所有带标签的节点计算cross entropy损失函数：

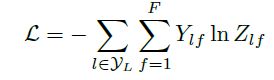
就可以训练一个node classification的模型了。由于即使只有很少的node有标签也能训练，作者称他们的方法为半监督分类。

GCN实战解决“空手道俱乐部问题”

问题概述

空手道俱乐部是一个包含34个成员的社交网络，有成对的文档交互发生在成员之间。俱乐部后来分裂成两个群体，分别以指导员（节点0）和俱乐部主席（节点33）为首，整个网络可视化如下图：

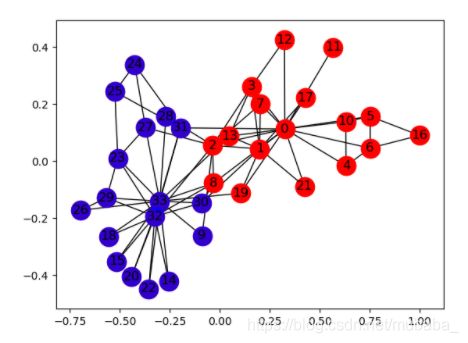
任务是预测每个节点会加入哪一边。
创建club图如下：

import dgl

def build_karate_club_graph():
    g = dgl.DGLGraph()
    # add 34 nodes into the graph; nodes are labeled from 0~33
    g.add_nodes(34)
    # all 78 edges as a list of tuples
    edge_list = [(1, 0), (2, 0), (2, 1), (3, 0), (3, 1), (3, 2),
        (4, 0), (5, 0), (6, 0), (6, 4), (6, 5), (7, 0), (7, 1),
        (7, 2), (7, 3), (8, 0), (8, 2), (9, 2), (10, 0), (10, 4),
        (10, 5), (11, 0), (12, 0), (12, 3), (13, 0), (13, 1), (13, 2),
        (13, 3), (16, 5), (16, 6), (17, 0), (17, 1), (19, 0), (19, 1),
        (21, 0), (21, 1), (25, 23), (25, 24), (27, 2), (27, 23),
        (27, 24), (28, 2), (29, 23), (29, 26), (30, 1), (30, 8),
        (31, 0), (31, 24), (31, 25), (31, 28), (32, 2), (32, 8),
        (32, 14), (32, 15), (32, 18), (32, 20), (32, 22), (32, 23),
        (32, 29), (32, 30), (32, 31), (33, 8), (33, 9), (33, 13),
        (33, 14), (33, 15), (33, 18), (33, 19), (33, 20), (33, 22),
        (33, 23), (33, 26), (33, 27), (33, 28), (33, 29), (33, 30),
        (33, 31), (33, 32)]
    # add edges two lists of nodes: src and dst
    src, dst = tuple(zip(*edge_list))
    g.add_edges(src, dst)
    # edges are directional in DGL; make them bi-directional
    g.add_edges(dst, src)

    return g

给边和节点赋予特征，使用一个feature张量在第一维上一次性给所有的节点添加特征：

import torch

G.ndata['feat'] = torch.eye(34)

定义一个GCN：

import torch.nn as nn
import torch.nn.functional as F

# 主要定义message方法和reduce方法
# NOTE: 为了易于理解，整个教程忽略了归一化的步骤
def gcn_message(edges):
    # 参数：batch of edges
    # 得到计算后的batch of edges的信息，这里直接返回边的源节点的feature.
    return {'msg' : edges.src['h']}

def gcn_reduce(nodes):
    # 参数：batch of nodes.
    # 得到计算后batch of nodes的信息，这里返回每个节点mailbox里的msg的和
    return {'h' : torch.sum(nodes.mailbox['msg'], dim=1)}

# Define the GCNLayer module
class GCNLayer(nn.Module):
    def __init__(self, in_feats, out_feats):
        super(GCNLayer, self).__init__()
        self.linear = nn.Linear(in_feats, out_feats)

    def forward(self, g, inputs):
        # g 为图对象； inputs 为节点特征矩阵
        # 设置图的节点特征
        g.ndata['h'] = inputs
        # 触发边的信息传递
        g.send(g.edges(), gcn_message)
        # 触发节点的聚合函数
        g.recv(g.nodes(), gcn_reduce)
        # 取得节点向量
        h = g.ndata.pop('h')
        # 线性变换
        return self.linear(h)

再定义一个更深的GCN模型，包含两层 GCN层：

class GCN(nn.Module):
    def __int__(self, in_feats, hidden_size, num_classes):
        super(GCN, self).__int__()
        self.gcn1 = GCNLayer(in_feats, hidden_size)
        self.gcn2 = GCNLayer(hidden_size, num_classes)
        
    def forward(self, g, inputs):
        h = self.gcn1(g, inputs)
        h = torch.relu(h)
        h = self.gcn2(g, h)
        return h

# 以空手道俱乐部为例
# 第一层将34层的输入转化为隐层为5
# 第二层将隐层转化为最终的分类数2
net = GCN(34,5,2)

使用one-hot向量初始化节点。因为是一个半监督的设定，仅有指导员（节点0）和俱乐部主席（节点33）被分配了label：

inputs = torch.eye(34)
labeled_nodes = torch.tensor([0, 33])  # only the instructor and the president nodes are labeled
labels = torch.tensor([0, 1])  # their labels are different

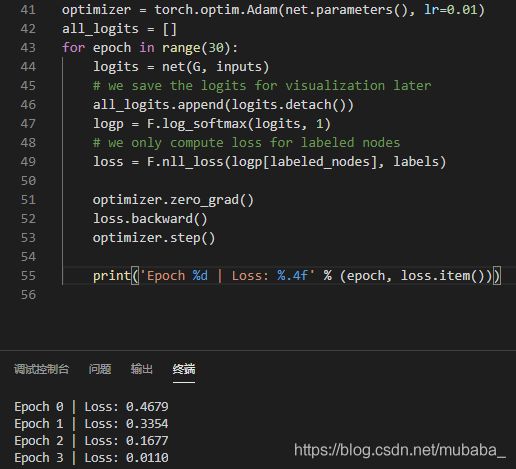
训练：

optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
all_logits = []
for epoch in range(30):
    logits = net(G, inputs)
    # we save the logits for visualization later
    all_logits.append(logits.detach())
    logp = F.log_softmax(logits, 1)
    # we only compute loss for labeled nodes
    loss = F.nll_loss(logp[labeled_nodes], labels)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print('Epoch %d | Loss: %.4f' % (epoch, loss.item()))

结果：