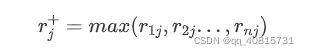权重设计：客观赋权法的说明（熵权法/变异系数法/CRCIII法/TOPSIS法）

在数据分析中，我们经常会遇到多个特征对于结果造成不同影响的情况，如何识别这些特征各自的权重，对我们的后续结果评估，打分矩阵构建都具有重要意义。我们所说的赋权法是用于解决多指标综合评价问题中的各指标权重大小关系。

确定指标权重的方法主要分成两大类，第一类是主观赋权法，这类方法主要从个人主观的看法和经验出发，比如专家评分法。另外一类就是客观赋权法，比如熵权法、标准离差法和CRⅢC法，接下来将做详细介绍。

熵值法与TOPSIS法以及两者结合_卖山楂啦prss的博客-CSDN博客_topsis综合评价法和熵权法

python脚本用法下篇博客进行讲解！

一、熵权法

熵权法 —— python_洋洋菜鸟的博客-CSDN博客_python熵权法

熵在我们的信息论中其实提及较多，一般我们认为如果某个指标的信息熵E越小，就表明其指标的变异程度越大，提供的信息量也越大。 可以理解成其信息熵也就越大，其权重也就越大。

再次解释：离散程度大，信息量大，不确定性小，则熵也就越小；信息量少，不确定性大，熵也越大。可以通过熵值来判断某个指标的离散程度，离散程度越大，该指标对综合评价影响越大。

下面就是我们信息熵的计算公式：

其中m为被评价对象的数目(我们的例子就是4)，n为评价指标数目(我们的例子为5)，其中我们每个方案的每个指标值用f_ij表示，i表示第i个案例，j表示第j个指标，且用d_ij表示指标值的标准化后的数值：

熵权法基本操作步骤如下：

二、标准离差法

变异系数法之python_洋洋菜鸟的博客-CSDN博客_变异系数python

标准离差法其实在我们统计学中是使用得比较多的，也是容易理解的一种方法。我们可以认为如果某个指标的标准差越大，就表示该指标的变异程度越大，提供的信息量就越大，在评价中起到的作用也就越大，权重也就越大。利用标准差计算各指标的权重公式如下：

同样地用R语言实现计算过程，过程相对于熵权法就简单很多了。

# 标准离差法

std = apply(data,2,sd)

W2 = std/sum(std)

三、CRIII C法

CRITIC法之python_洋洋菜鸟的博客-CSDN博客

CRIII C法的思路是确定两个客观指标数，一是对比强度，它表示了同一个指标不同评价方案之间取差距的大小，以标准差的形式来表现，即标准化的大小表明了同一个指标内各方案取值差距的大小，标准差越大各方案之间取值差距越大；二是评价指标之间的冲突性，指标之间的冲突性是以指标之间的相关性为基础，如果各个指标之间具有较强的正相关，说明两个指标冲突性低。

对比性：

矛盾性：

信息承载量：

继续使用R语言实现计算过程。

C_j= apply(1-cor(data),2,sum)*std

W3 = C_j/sum(C_j)

我们得到三种不同的权重方案之后，之后就是计算各购车方案在三种权重方案下的得分，结果如下：

三种客观赋权法中，熵权法和标准离差法的基本思路相似，都是通过根据指标变异性的大小来确定客观权重。而CRⅢC法不仅考虑了指标变异大小对权重的影响，还考虑了各指标之间的冲突性，因此可以说CRⅢC法是一种比熵权法和标准离差法更好的客观赋权法

对于CRⅢC法而言，在标准差一定时，指标间冲突性越小，权重也越小，也就是说当两个指标间的正相关程度越大时，那么它们的冲突性越小，这表明两个指标在评价方案的优劣上反映的信息有较大的相似性。因此，当对选取指标比较多的项目进行评价时，可以在正相关程度较高的指标中去除一些指标，这样可以减少计算量而不会多评价结果产生很大的影响。

四、TOPSIS法（逼近理想解排序法、优劣解距离法）

TOPSIS法 —— python_洋洋菜鸟的博客-CSDN博客_python topsis

TOPSIS是通过逼近理想解的程度来评估各个样本的优劣等级 

TOPSIS法的基本原理：在归一化后的原始数据矩阵中，找到有限方案中最优方案和最劣方案，然后分别计算评价对象与最优方案和最劣方案之间的距离，并以此为依据来评价样本的优劣等级。

假设有n个待评价样本，p项评价指标，形成原始指标数据矩阵：

步骤为：

1）数据标准化

2）计算信息熵和权重

3）确定正理想解和负理想解

处理后可以构成数据矩阵 R=（rij）m*n

定义每个指标每列的最大值为正理想解：

定义每个指标每列的最小值为负理想解：

 

4）计算各个方案得到的正（负）理想解的距离

定义第i个对象与最大值距离为正理想解的距离

 

定义第i个对象与最大值距离为负理想解的距离

5）计算综合评价值

明显可以看出0<=score<=1 ，当scorei越大时，d+越小，说明指标离最大值距离越小，越接近最大值

五、组合赋权法