fisher信息矩阵_经典模式识别：Fisher线性判别

本文将介绍Fisher线性判别的原理和具体实践，阅读时间约8分钟，关注公众号可在后台领取数据集资源哦^-^

Fisher线性判别

1.背景介绍

生活中我们往往会遇到具有高维特性的数据，如个人信息，天气数据等。而在使用统计方法处理分类等模式识别问题时，通常是在低维空间展开研究的。而一般基于统计学习方法难以求解高维数据，所以降维成了解决问题的突破口。

对于高维空间样本，投影到一维坐标上，可能会出现样本特征混杂的现象，这将难以进行分类。如果寻找一个投影方向，使得样本集合在该投影方向最易区分，找寻这个最优方向的过程就是Fisher线性判别所解决的问题。

Fisher判别法的基本思想是将 类维数据集尽可能地投影到一条直线方向，使得类与类之间尽可能分开，再通过确定一个分类阈值来进行分类。

2.模型建立及求解方法

2.1基本参量

假设有个N1属于类的n维样本以及N2个属于类的n维样本，将两者合并成一个集合。经线性组合可得标量：

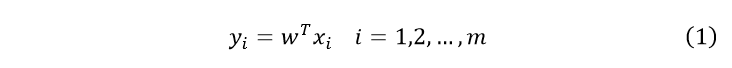
下面定义几个基本参量。在n维X空间中：

1. 各类样本均值：

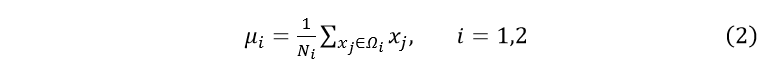
    2.各类类内离散度矩阵：

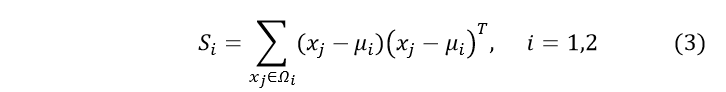
    3.总类内离散度矩阵：

同理我们可以求得在一维Y空间中的各类样本均值，各类类内离散度以及总类内离散度矩阵。此处不再赘述。

2.2求解

Fisher判别想要尽可能地在一维空间分开样本，需要使各类类间差异性尽可能大(均值差尽可能大)，同时类内离散度尽可能小。根据这一思想，我们可以设立如下准则函数：

通过推导(此处省略，详细过程可参考《模式识别》西安电子科技大学出版社)，可以求出最优投影方向：

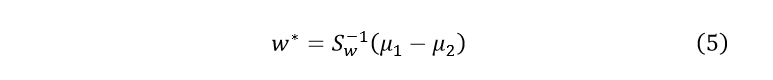
我们可以将任意未知样本投影到该一维方向上：

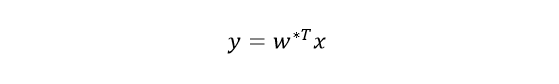
此时我们还需要设定一个阈值来对一维方向上的样本进行划分。此处我们采用

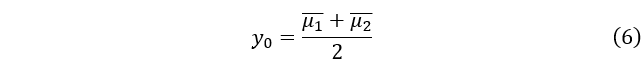
其中，

是投影到一维方向后两类样本各自的均值。

根据公式(6)，我们可以对降维后的样本进行分类。

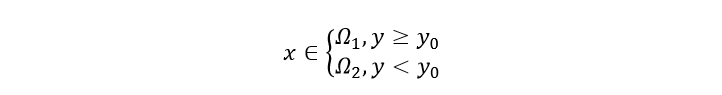
当样本投影到一维后的y值大于y0时，样本属于第一类，反之属于第二类。

3.实验

3.1实验环境

本文使用python3.7进行编程仿真，并使用了sklearn、numpy、matplotlib等python库。

3.2iris数据集分类问题

iris数据集中包含了3类鸢尾花特征数据。每一类分别有50条样本，每条样本有4个维度的特征数据(花萼长度，花萼宽度，花瓣长度，花瓣宽度)。首先我们先对数据集进行可视化观察。

我们对花萼长度、宽度这两个特征，对150条样本进行比较。如下图所示，可以发现第一类鸢尾花与第二、三两类区分较大，可以通过一条直线来较好地划分。而第二、三两类鸢尾花之间在花萼宽度上差异较小，难以直接区分，第三类鸢尾花的花萼长度整体较长。

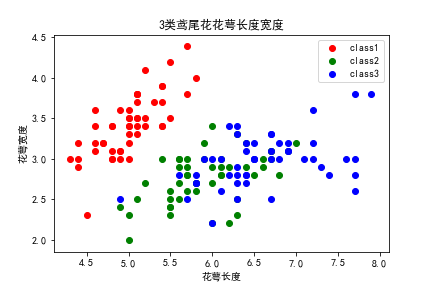
再对花瓣长度、宽度两个特征进行可视化比较。如下图所示，可以发现三类鸢尾花在这两个特征上区分较为明显，可以较为容易的进行区分。

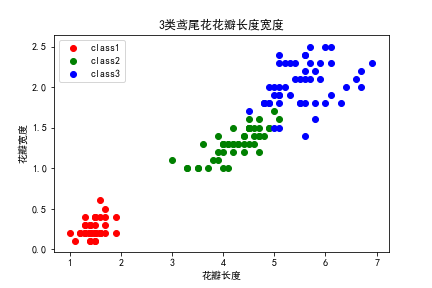
然后，我们对每两类样本分别进行fisher线性判别分类，并分别计算正确率。以第二类和第三类数据为例，先分别从两类样本中随机选取30个样本作为训练集，剩余的20个样本作为测试集。通过2.2中求解方法对最优方向w进行求解，将样本数据投影到该方向上的一维直线上，效果如下图所示：

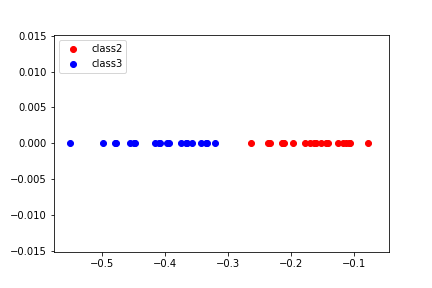
红色的代表第一类鸢尾花，蓝色代表第二类鸢尾花。可以发现，样本已经较好地被区分为两类。

根据公式(6)可计算得到阈值，可以将测试样本进行完全的区分，正确率为100%。

对三类数据样本两两进行分类，并将每两组10次测试结果的正确率求平均值作为最终正确率。可以得到下表：

可以看出，第一、二类和第一、三类鸢尾花都可以被很好地区分开，分类正确率稳定在100%；而第二、三类在某些情况下会出现错误分类的样本，但整体正确率仍然较高，达到94.25%。

由此可见，Fisher线性判别在iris数据集上能够取得较好的分类效果。

3.2sonar数据集分类问题

Sonar数据集共207条样本，每个样本含有60维的特征。样本分为R、M两类，其中R类样本有96条，M样本有111条。

与3.1相同，我们分别将R、M两类样本的60%作为训练集，剩下的作为测试集。其中R类测试样本为39条，M类测试样本为45条。

由于我们不确定以多少维特征进行Fisher线性判别分类效果较好，所以我们从采用随机抽取1维到60维特征的方式不断测试，计算采用不同维数的特征时的分类正确率，重复实验二十次。并将20次实验的平均值作为采用不同特征纬度下Fisher线性判别的分类正确率。

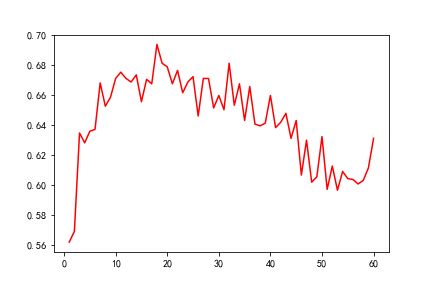
最终，我们得到的实验效果图如下：

从中，我们可以看出从采用一维特征进行分类到采取18维特征，正确率不断上升，最高可达到70.2%左右；但采用维数超过18维后，分类正确率开呈现波动下降趋势。

我们对数据集进行重新划分，观察训练样本数量对分类效果的影响。我们分别采用占总数据集70%，60%(上文实验)，50%的训练样本进行训练，并在剩余样本中测试正确率。第一、三组实验结果如下：

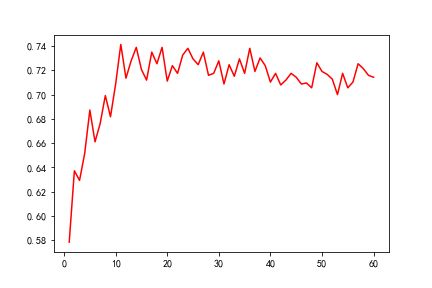
第一组(70%)

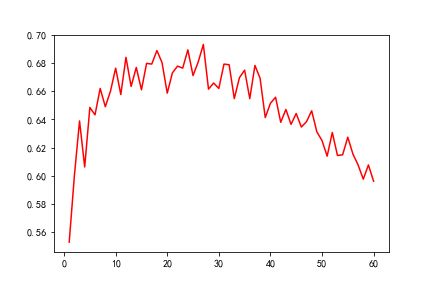
第二组(50%)

可以发现当增加训练样本数量时，测试正确率整体上升，正确率最高上升至74.2%，且当增加样本维数时正确率趋于稳定，稳定在72%左右；当减少训练样本数量时，无明显的改善情况，整体变化趋势与第二组实验接近。

在本问题中，考虑两类测试样本的数量不同，我们采用下式计算新的阈值。

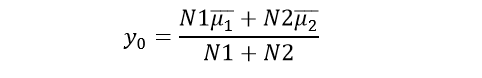
再次进行实验，训练、测试集比例为3:2。我们可以发现分类正确率并未改善。

4.思考

Fisher线性判别在对复杂样本降维分类的情况中具有重要作用。在对维数少的样本进行分类时，Fisher线性判别往往能起到较好的效果；在对维数较高的样本分类时，特征冗余度上升，投影到一维直线后区分难度大大提高，正确率降低或无法再继续上升。在实际分类时，我们需要对训练、测试样本的比例进行实验，更多的训练样本可能会提升分类的正确率，但也有可能造成过拟合现象，降低Fisher线性判别的泛化能力。

在处理维数较多数据时，我们可对特征先进行主成分分析等关联度分析方法，降低数据维数，再进行Fisher线性判别，可能可以取得更理想的效果，此处不再过多论述。

5.代码及数据集获取

sklearn包自带iris数据集，本文直接导入。sonar数据集可关注微信公众号后在后台回复sonar领取。代码已上传作者的github。

https://github.com/zoukeh/Fisher

上文2.2中最优投影方向公式推导可参考https://blog.csdn.net/bless2015/article/details/104765976(如有侵权请告知)

作者水平有限，若有错误敬请指正。请多多支持关注哦^-^