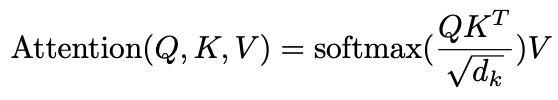逐句解析点积注意力pytorch源码（配图解）

前言

结合pytorch源码和原始论文学习Scaled Dot-Product Attention的原理。

原论文链接：Attention Is All You Need
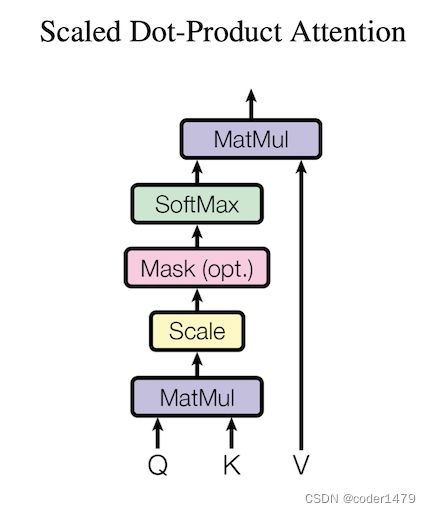
原论文中的网络结构如下图所示。

计算公式

源码（pytorch）

# 以下代码来自pytorch源码
def _scaled_dot_product_attention(
    q: Tensor,
    k: Tensor,
    v: Tensor,
    attn_mask: Optional[Tensor] = None,
    dropout_p: float = 0.0,) -> Tuple[Tensor, Tensor]:  
  
    B, Nt, E = q.shape
    q = q / math.sqrt(E)    
    # (B, Nt, E) x (B, E, Ns) -> (B, Nt, Ns)
    attn = torch.bmm(q, k.transpose(-2, -1))    

    if attn_mask is not None:        
        attn += attn_mask
    
    attn = softmax(attn, dim=-1)

    if dropout_p > 0.0:
        attn = dropout(attn, p=dropout_p)
    # (B, Nt, Ns) x (B, Ns, E) -> (B, Nt, E)
    output = torch.bmm(attn, v)
    return output, attn

下面逐句解读。

第一步：实现scaled

q = q / math.sqrt(E)    

其中的math.sqrt(E)对应计算公式中的$\sqrt{d_k}$。

根据源码，E（也就是$d_k$）代表Q、K、V三个张量中特征（embedding）的维度。

关于Q、K、V的形状的代码注释。

• q: :math:(B, Nt, E) where B is batch size, Nt is the target sequence length,
  and E is embedding dimension.
• key: :math:(B, Ns, E) where B is batch size, Ns is the source sequence length,
  and E is embedding dimension.
• value: :math:(B, Ns, E) where B is batch size, Ns is the source sequence length,
  and E is embedding dimension.

在论文中对Q、K、V维度的说明：

The input consists of queries and keys of dimension $d_k$ , and values of dimension $d_v$ .

为什么要除以$\sqrt{d_k}$？

原论文中的解释如下：

While for small values of $d_k$ the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of $d_k$ . We suspect that for large values of $d_k$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients . To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d_k}}$

简单解释就是：当 $d_k$ 较大时（也就是Q和K的维度较大时），dot-product attention的效果就比加性注意力差。作者推测，对于较大的$d_k$值，点积（Q和K的转置的点积）的增长幅度很大，进入到了softmax函数梯度非常小的区域。

李沐老师在Transformer论文逐段精读【论文精读】中对这部分的解读摘录如下：

当你的dk不是很大的时候，除不除都没关系。
但是当dk很大的时候，也就是说两个向量比较长的时候，那么你做点积的时候，这些值呢，就可能会比较大，但也可能是比较小。
当你的值相对来说比较大的时候呢，你之间的相对的差距就会变大，就导致说，你值最大的那个值做出来softmax就会更加靠近1。剩下那些值呢就会更加靠近0。就是你的值更加向两端靠拢。当你出现这个样子的时候，你算梯度的时候，你发现梯度比较小。
因为softmax最后的结果是什么？就是我希望我的预测值啊，置信的地方尽量靠近1，不置信的地方尽量靠近0。这样子我的收敛就差不多了。这时候你的梯度就会变得比较小，那你就会跑不动。

softmax公式
$$softmax(x_i)=\frac{e^{x_i}}{{\sum }_{j=1}^K{e}^{x_j}}fori=1,2,\dots ,K$$

更详细计算建议参考https://blog.csdn.net/qq_37430422/article/details/105042303

为什么先除以$\sqrt{d_k}$？

为什么不按照公式，先计算$Q{K}^T$矩阵乘法，再除以$\sqrt{d_k}$呢？
从数值计算的角度考虑，要尽量控制数值的大小，这样可以保持浮点数的精度。
也就是说，先计算除法，后面计算矩阵乘法的时候，误差就更小。

第二步：通过点积（dot product）计算注意力分数

    # (B, Nt, E) x (B, E, Ns) -> (B, Nt, Ns)
    attn = torch.bmm(q, k.transpose(-2, -1)) 

计算q和$k^T$的乘积。bmm是批量矩阵乘法。
其中k.transpose(-2, -1)表示交换k的倒数第1和倒数第2维度，保持批量维度不变。

第三步：mask

    if attn_mask is not None:        
        attn += attn_mask

在解码阶段，要限制未来的数据影响，只保留当前时刻之前的数据，所以一般加上一个负无穷大的数，这样后面计算softmax的时候，相应的结果就是0，起到mask的效果。

第四步：计算注意力权重

attn = softmax(attn, dim=-1)

经过softmax之后，attn就称为注意力权重了，因为归一化了。

其中的dim=-1，表示对最后一个维度进行softmax，也就是词向量维度。

第五步：dropout

    if dropout_p > 0.0:
        attn = dropout(attn, p=dropout_p)

注：Transformer原始论文中的dropout_p=0.1。

第六步：加权平均

    # (B, Nt, Ns) x (B, Ns, E) -> (B, Nt, E)
    output = torch.bmm(attn, v)
    return output, attn

V和注意力权重相乘，并返回结果。

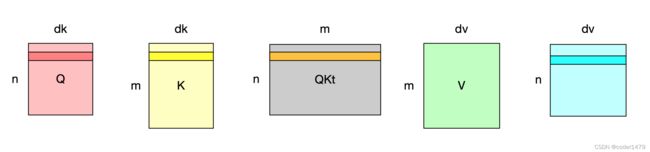
图解QKV矩阵乘法

注意：这里不再使用源码中矩阵shape的符号。

Q是n乘以dk的矩阵，代表多个Querys，理解为每行一个query向量。
K是m乘以dk的矩阵，代表多个Keys，理解为每行一个key向量。
Q和K的转置相乘，得到的矩阵中每一行（橙色的行）代表某一个query向量和所有key向量之间的相似度，也就是一个query向量和所有key向量点积。
灰色矩阵实际上就是相关度矩阵，注意力分数矩阵。

V是m乘以dv的矩阵，代表多个Values，每行代表一个value向量。
橙色向量左乘V，代表V的行向量按照橙色向量的权重进行线性组合，得到蓝色向量。