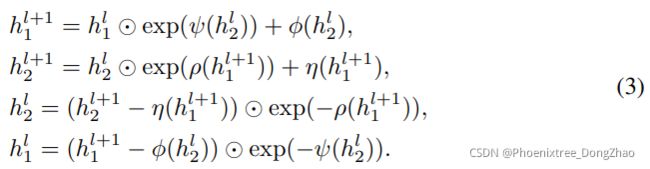可逆图像缩放 ECCV 2020 :Invertible Image Rescaling
Invertible Image Rescaling
https://arxiv.org/pdf/2005.05650.pdf![]() https://arxiv.org/pdf/2005.05650.pdfhttps://github.com/pkuxmq/Invertible-Image-Rescaling
https://arxiv.org/pdf/2005.05650.pdfhttps://github.com/pkuxmq/Invertible-Image-Rescaling![]() https://github.com/pkuxmq/Invertible-Image-Rescaling
https://github.com/pkuxmq/Invertible-Image-Rescaling
目录
Invertible Image Rescaling
Abstract
Introduction
Related Work
Methods
Post 讲解
Abstract
High-resolution digital images are usually downscaled to fit various display screens or save the cost of storage and bandwidth, meanwhile the post-upscaling is adpoted to recover the original resolutions or the details in the zoom-in images. However, typical image downscaling is a non-injective mapping due to the loss of high-frequency information, which leads to the ill-posed problem of the inverse upscaling procedure and poses great challenges for recovering details from the downscaled low-resolution images. Simply upscaling with image super-resolution methods results in unsatisfactory recovering performance.
In this work, we propose to solve this problem by modeling the downscaling and upscaling processes from a new perspective, i.e. an invertible bijective transformation, which can largely mitigate the ill-posed nature of image upscaling. We develop an Invertible Rescaling Net (IRN) with deliberately designed framework and objectives to produce visually-pleasing low-resolution images and meanwhile capture the distribution of the lost information using a latent variable following a specified distribution in the downscaling process. In this way, upscaling is made tractable by inversely passing a randomly-drawn latent variable with the low-resolution image through the network.
Experimental results demonstrate the significant improvement of our model over existing methods in terms of both quantitative and qualitative evaluations of image upscaling reconstruction from downscaled images.
提出动机:从应用(在不同显示器上显示,节约存储和宽带成本)出发提出需求,到目前上采样(downscaling 是非单射匹配,upscaling 会丢失细节)和超分算法(恢复效果不理想)的不足。
本文工作:提出可逆双射变换,构建 Invertible Rescaling Net (IRN) 网络。至于该网络为啥有效,作者的这里的一句解释很抽象。。。
实验结论:就是很好地解决了 downscaled 图像的 upscaling 重构问题。
Introduction
第一段(略了):研究背景需求和 upscaling 的问题所在,提出研究背景。
第二段(略了):传统超分算法的问题。
第三段(略了):联合 downscaling 和 upscaling 方法 [26] [34] [49] 的问题。
[26] ECCV18 : Task-aware image downscaling;
[34] TIP18 : Learning a convolutional neural network for image compact-resolution
[49] TIP18 : Learned image downscaling for upscaling using content adaptive resampler
In this paper, with inspiration from the reciprocal nature of this pair of image rescaling tasks, we propose a novel method to largely mitigate this ill-posed problem of the image upscaling. According to the Nyquist-Shannon sampling theorem, high-frequency contents are lost during downscaling. Ideally, we hope to keep all lost information to perfectly recover the original HR image, but storing or transferring the high-frequency information is unacceptable. In order to well address this challenge, we develop a novel invertible model called Invertible Rescaling Net (IRN) which captures some knowledge on the lost information in the form of its distribution and embeds it into model’s parameters to mitigate the ill-posedness. Given an HR image
, IRN not only downscales it into a visually-pleasing LR image
, but also embed the case-specific high-frequency content into an auxiliary case-agnostic latent variable
, whose marginal distribution obeys a fixed pre-specified distribution (e.g., isotropic Gaussian). Based on this model, we use a randomly drawn sample of
from the pre-specified distribution for the inverse upscaling procedure , which holds the most information that one could have in upscaling.
downscale 和 upscale 是一对互补的过程。
奈奎斯特-香浓定理说明,downscale 过程一定会丢失信息,这些信息在 upscale 过程是无法完全恢复的。
本文的思路是,在 downscale 的过程中,除了得到高质量的 LR 图像,同时也要将特定案例的高频内容嵌入到一个辅助的不可知案例的潜在变量中,而这个变量的边际分布服从一个固定的预先指定的分布,如各向同性高斯分布。
基于此模型,本文的方法从预先指定的分布中随机抽取 ![]() 样本进行逆 upscaling 过程,其中包含了 upscaling 过程中所能获得的更多信息。
样本进行逆 upscaling 过程,其中包含了 upscaling 过程中所能获得的更多信息。
Yet, there are still several great challenges needed to be addressed during the IRN training process. Specifically, it is essential to ensure the quality of reconstructed HR images, obtain visually pleasing downscaled LR ones, and accomplish the upscaling with a case-agnostic
, i.e.,
instead of a case-specific
.
To this end, we design a novel compact and effective objective function by combining three respective components: an HR reconstruction loss, an LR guidance loss and a distribution matching loss. The last component is for the model to capture the true HR image manifold as well as for enforcing
to be case-agnostic.
Neither the conventional adversarial training techniques of generative adversarial nets (GANs) [21] nor the maximum likelihood estimation (MLE) method for existing invertible neural networks [15,16,29,4] could achieve our goal, since the model distribution doesn’t exist here, meanwhile these methods don’t guide the distribution in the latent space.
Instead, we take the pushed-forward empirical distribution of
as the distribution on
, which, in independent company with
, is the actually used distribution to inversely pass our model to recover the distribution of
. We thus match this distribution with the empirical distribution of
(the data distribution).
Moreover, due to the invertible nature of our model, we show that once this matching task is accomplished, the matching task in the
space is also solved, and
is made case-agnostic.
We minimize the JS divergence to match the distributions, since the alternative sample-based maximum mean discrepancy (MMD) method [3] doesn’t generalize well to the high dimension data in our task.
这一大段故事包括以下几点:
本文方法需要面临的难题是:保证重建的HR图像的质量;获得视觉上令人满意的缩小的 LR 图像;并使用案例无关的 ![]() 来完成 upscaling,即
来完成 upscaling,即 ![]() 而不是案例特定的
而不是案例特定的 ![]() ,这是至关重要的。
,这是至关重要的。
为此,本文提出了一个密集的目标函数,包括 an HR reconstruction loss, an LR guidance loss and a distribution matching loss。
最后一个 loss 是为了让模型捕获真正的 HR 图像流形,以及强制 ![]() 是个案无关的。
是个案无关的。
生成对抗网络的传统对抗训练技术和已有可逆神经网络的最大似然估计(MLE)方法都不能达到我们的目标,因为这里不存在模型分布,同时这些方法也不能指导潜在空间的分布。
本文将 ![]() 的 pushed-forward 经验分布作为
的 pushed-forward 经验分布作为 ![]() 的分布,且这个分布与
的分布,且这个分布与 ![]() 相独立,同时也是反向可逆过程中恢复
相独立,同时也是反向可逆过程中恢复 ![]() 使用的分布。因此,将这个分布与
使用的分布。因此,将这个分布与 ![]() 的经验分布 (数据分布) 相匹配。
的经验分布 (数据分布) 相匹配。
此外,由于模型的可逆性质,本文证明一旦这个匹配任务完成,![]() 空间中的匹配任务也会被解决,并且
空间中的匹配任务也会被解决,并且 ![]() 是不区分大小写的。
是不区分大小写的。
本文采用最小化 JS 发散来匹配分布,因为替代的基于样本的最大平均偏差 (MMD) 方法不能很好地推广到本任务中的高维数据。
Our contributions are concluded as follows:
– To our best knowledge, the proposed IRN is the first attempt to model image downscaling and upscaling, a pair of mutually-inverse tasks, using an invertible (i.e., bijective) transformation. Powered by the deliberately designed invertibility, our proposed IRN can largely mitigate the ill-posed nature of image upscaling reconstruction from the downscaled LR image.
– We propose a novel model design and efficient training objectives for IRN to enforce the latent variable
, with embedded lost high-frequency information in the downscaling direction, to obey a simple case-agnostic distribution. This enables efficient upscaling based on the valuable samples of
drawn from the certain distribution.
– The proposed IRN can significantly boost the performance of upscaling reconstruction from downscaled LR images compared with state-of-the-art downscaling-SR and encoder-decoder methods. Moreover, the amount of parameters of IRN is significantly reduced, which indicates the light-weight and high-efficiency of the new IRN model.
贡献总结为:
首次用可逆变换解决 downscaling and upscaling 问题;
提出了高效的目标函数,强制潜变量 ![]() ,在 downscaling 方向上嵌入丢失的高频信息,服从简单的案例不可知分布(非常重要的创新);
,在 downscaling 方向上嵌入丢失的高频信息,服从简单的案例不可知分布(非常重要的创新);
性能好,还参数少。
Related Work
Image Upscaling after Downscaling
Super resolution (SR) is a widely-used image upscaling method and get promising results in low-resolution (LR) image upscaling task. Therefore, SR methods could be used to upscale downscaled images. Since the SR task is inherently ill-posed, previous SR works mainly focus on learning strong prior information by example-based strategy [18,20,46,27] or deep learning models [17,36,60,59,14,50]. However, if the targeted LR image is pre-downscaled from the corresponding high-resolution image, taking the image downscaling method into consideration would significantly help the upscaling reconstruction.
Traditional image downscaling approaches employ frequency-based kernels, such as Bilinear, Bicubic, etc. [41], as a low-pass filter to sub-sample the input HR images into target resolution. Normally, these methods suffer from resulting over-smoothed images since the high-frequency details are suppressed. Therefore, several detail-preserving or structurally similar downscaling methods [31,42,51,52,38] are proposed recently. Besides those perceptual-oriented downscaling methods, inspired by the potentially mutual reinforcement between downscaling and its inverse task, upscaling, increasing efforts have been focused on the upscaling-optimal downscaling methods, which aim to learn a downscaling model that is optimal to the post-upscaling operation.
For instance, Kim et al. [26] proposed a task-aware downscaling model based on an auto-encoder framework, in which the encoder and decoder act as the downscaling and upscaling model, respectively, such that the downscaling and upscaling processes are trained jointly as a united task. Similarly, Li et al. [34] proposed to use a CNN to estimate downscaled compact-resolution images and leverage a learned or specified SR model for HR image reconstruction. More recently, Sun et al. [49] proposed a new content-adaptive-resampler based image downscaling method, which can be jointly trained with any existing differentiable upscaling (SR) models.
Although these attempts have an effect of pushing one of downscaling and upscaling to resemble the inverse process of the other, they still suffer from the ill-posed nature of image upscaling problem. In this paper, we propose to model the downscaling and upscaling processes by leveraging the invertible neural networks.
传统的 downscaling 方法采用 frequency based kernels;这种方法直接将细节信息丢失了。
所以,为了保留细节信息,detail-preserving or structurally similar downscaling 被提出。
另外,为了能让 downscaling 图像 upscaling 更好的图像,提出了能让 upscaling 最优的 downscaling 方法,即 upscaling-optimal downscaling methods。
例如 。。。。
尽管这些尝试具有推动 downscaling 和 upscaling 的效果,以类似于另一个的逆过程,他们仍然遭受图像 upscaling 不适定这个本质的问题。
Invertible Neural Network
The invertible neural network (INN) [15,16,29,32,22,8,13] is a popular choice for generative models, in which the generative process
given a latent variable
can be specified by an INN architecture
. The direct access to the inverse mapping
makes inference much cheaper. As it is possible to compute the density of the model distribution in INN explicitly, one can use the maximum likelihood method for training. Due to such flexibility, INN architectures are also used for many variational inference tasks [44,30,10].
可逆神经网络 (INN) 是生成模型的常用选择,其中 用 INN 体系结构 ![]() 实现潜在变量
实现潜在变量 ![]() 的生成过程
的生成过程 ![]() 。逆映射为
。逆映射为 ![]() 。
。
由于可以在 INN 中明确地计算模型分布的密度,可以使用最大似然法进行训练。
由于这种灵活性,INN体系结构也被用于许多变分推理任务。
INN is composed of invertible blocks. In this study, we employ the invertible architecture in [16]. For the l-th block, input
is split into
and
along the channel axis, and they undergo the additive affine transformations [15]:
where φ, η are arbitrary functions. The corresponding output is
. Given the output, its inverse transformation is easily computed:
To enhance the transformation ability, the identity branch is often augmented [16]:
这里给出了一种 INN 模型,是 ICLR 2017 一篇文章中给出的模型。至于为啥这样,有啥好处,请参拜原著:
[16] Density estimation using real NVP [2017 ICLR]https://arxiv.org/pdf/1605.08803.pdf![]() https://arxiv.org/pdf/1605.08803.pdf
https://arxiv.org/pdf/1605.08803.pdf
Some prior works studied using INN for paired data
. Ardizzone et al. [3] analyzed real-world problems from medicine and astrophysics. Compared to their tasks, image downscaling and upscaling bring more difficulties because of notably larger dimensionality, so that their losses do not work for our task. In addition, the ground-truth LR image y does not exist in our task. Guided image generation and colorization using INN is proposed in [4] where the invertible modeling between
and
is conditioned on a guidance
. The model cannot generate
given
thus is unsuitable for the image upscaling task. INN is also applied to the image-to-image translation task [43] where the paired domain
instead of paired data is considered, thus is again not the case of image upscaling.
[3] Analyzing inverse problems with invertible neural networks [2019 ICLR][4] Guided image generation with ¨ conditional invertible neural networks [2019]
[43] Reversible gans for memory-efficient image-to-image translation [2019 CVPR]
一些先前的工作使用 INN 对配对数据 (x, y) 进行了研究。Ardizzone 等人分析了来自医学和天体物理学的现实问题。与他们的任务相比,图像的降维和升维明显更大,带来了更多的困难,所以他们的损失对我们的任务不起作用。此外,真实 LR 图像 ![]() 在本文的任务中不存在。在 [4] 中提出了使用 INN 的引导图像生成和着色,其中
在本文的任务中不存在。在 [4] 中提出了使用 INN 的引导图像生成和着色,其中 ![]() 和
和 ![]() 之间的可逆建模是以引导
之间的可逆建模是以引导 ![]() 为条件的。该模型不能在给定
为条件的。该模型不能在给定 ![]() 的情况下生成
的情况下生成 ![]() ,因此不适合图像的 upscaling 任务。INN 也应用于图像到图像的转换任务 [43],其中考虑的是成对的域 (X, Y) 而不是成对的数据,因此同样不是图像 upscaling 的情况。
,因此不适合图像的 upscaling 任务。INN 也应用于图像到图像的转换任务 [43],其中考虑的是成对的域 (X, Y) 而不是成对的数据,因此同样不是图像 upscaling 的情况。
Other Related Fields
- Image Compression
图像压缩是一种应用于数字图像的数据压缩,以降低其存储或传输成本。图像压缩可以是有损的(如JPEG、BPG) 或无损的 (如PNG、BMP)。近年来,基于深度学习的图像压缩方法在视觉效果和压缩比方面都有很好的效果。但是,图像的分辨率不会因压缩而改变,也就是说,压缩后的图像只有比特流 (bit-stream),没有视觉上有意义的低分辨率图像。因此,图像压缩方法无法满足我们的任务。
- Image Super-resolution
注意,图像的 upscaling 与超分辨率是不同的任务。在本文的场景中,真实的 HR 图像一开始是存在的,但在一些应用中,不得不暂时丢弃它,转而存储/传输 LR 版本。然后希望以后可以使用 LR图像恢复 HR 图像。而对于 SR,实际的 HR 在应用程序中是不存在的,任务是为LR生成新的HR图像。
Methods
Model Specification
The sketch of our modeling framework is presented in Fig. 1. As explained in Introduction, we mitigate the ill-posed problem of the upscaling task by modeling the distribution of lost information during downscaling. We note that according to the Nyquist-Shannon sampling theorem [47], the lost information during downscaling an HR image amounts to high-frequency contents. Thus we firstly employ a wavelet transformation to decompose the HR image ![]() into low and high-frequency component, denote as
into low and high-frequency component, denote as ![]() and
and ![]() respectively. Since the case-specific high-frequency information will be lost after downscaling, in order to best recover the original
respectively. Since the case-specific high-frequency information will be lost after downscaling, in order to best recover the original ![]() as possible in the upscaling procedure, we use an invertible neural network to produce the visually-pleasing LR image
as possible in the upscaling procedure, we use an invertible neural network to produce the visually-pleasing LR image ![]() meanwhile model the distribution of the lost information by introducing an auxiliary latent variable
meanwhile model the distribution of the lost information by introducing an auxiliary latent variable ![]() . In contrast to the case-specific
. In contrast to the case-specific ![]() (i.e.,
(i.e., ![]() ), we force
), we force ![]() to be case-agnostic (i.e.,
to be case-agnostic (i.e., ![]() ) and obey a simple specified distribution, e.g., an isotropic Gaussian distribution. In this way, there is no further need to preserve either
) and obey a simple specified distribution, e.g., an isotropic Gaussian distribution. In this way, there is no further need to preserve either ![]() or
or ![]() after downscaling, and
after downscaling, and ![]() can be randomly sampled in the upscaling procedure, which is used to reconstruct
can be randomly sampled in the upscaling procedure, which is used to reconstruct ![]() combined with LR image
combined with LR image ![]() by inversely passing the model.
by inversely passing the model.
模型定义:
首先,输入高分辨率图像通过 小波变换 分解为高频和低频成分;
然后,通过多个可逆神经网络做两件事,输出高质量 downscaling 图像 和 将失去的高频成分建模到一个辅助的潜在分布,这个分布与输入图像的任何成分无关,即为 case-agnostic,且服从 isotropic Gaussian 分布;这样做的好处是,网络不需要保存 ![]() 和
和 ![]() 的中间参数,在最后 upscaling 时,只需要 低分辨率图像和 isotropic Gaussian 分布随机采样的数据就可以恢复高质量高分辨率图像了。
的中间参数,在最后 upscaling 时,只需要 低分辨率图像和 isotropic Gaussian 分布随机采样的数据就可以恢复高质量高分辨率图像了。
Invertible Architecture
The general architecture of our proposed IRN is composed of stacked Downscaling Modules, each of which contains one Haar Transformation block and several invertible neural network blocks (InvBlocks), as illustrated in Fig. 2. We will show later that both of them are invertible, and thus the entire IRN model is invertible accordingly.
- The Haar Transformation
We design the model to contain certain inductive bias, which can efficiently learn to decompose
into the downscaled image
and case-agnostic high-frequency information embedded in
. To achieve this, we apply the Haar Transformation as the first layer in each downscaling module, which can explicitly decompose the input images into an approximate low-pass representation, and three directions of high-frequency coefficients [53][35][4]. More concretely, the Haar Transformation transforms the input raw images or a group of feature maps with height H, width W and channel C into a tensor of shape (1/2H, 1/2W, 4C). The first C slices of the output tensor are effectively produced by an average pooling, which is approximately a low-pass representation equivalent to the Bilinear interpolation downsampling. The rest three groups of C slices contain residual components in the vertical, horizontal and diagonal directions respectively, which are the high-frequency information in the original HR image. By such a transformation, the low and high-frequency information are effectively separated and will be fed into the following InvBlocks.
哈尔变换,er,不多讲了,很基础的东西。
- InvBlock
Taking the feature maps after the Haar Transformation as input, a stack of InvBlocks is used to further abstract the LR and latent representations. We leverage the general coupling layer architecture proposed in [15,16], i.e. Eqs. (1,3).
Utilizing the coupling layer is based on our considerations that (1) the input has already been split into low and high-frequency components by the Haar transformation; (2) we want the two branches of the output of a coupling layer to further polish the low and high-frequency inputs for a suitable LR image appearance and an independent and properly distributed latent representation of the high-frequency contents. So we match the low and high-frequency components respectively to the split of
,
in Eq. (1). Furthermore, as the short-cut connection is proved to be important in the image scaling tasks [36,50], we employ the additive transformation (Eq. 1) for the low-frequency part
, and the enhanced affine transformation (Eq. 3) for the high-frequency part
to increase the model capacity, as shown in Fig. 2.
1. 通过哈尔变换,输入已经被分解为低频和高频分量;
2. 低频分量作为公式(1)中的 ![]() ,高频分量作为
,高频分量作为 ![]() ;
;
3. 对于 ![]() 采用 additive transformation (Eq. 1);对于
采用 additive transformation (Eq. 1);对于 ![]() 采用 enhanced affine transformation (Eq. 3)。
采用 enhanced affine transformation (Eq. 3)。
Note that the transformation functions φ(·), η(·), ρ(·) in Fig. 2 can be arbitrary. Here we employ a densely connected convolutional block, which is referred as Dense Block in [50] and demonstrated for its effectiveness of image upscaling task. Function ρ(·) is further followed by a centered sigmoid function and a scale term to prevent numerical explosion due to the exp(·) function. Note that Figure 2 omits the exp(·) in function ρ.
其中,变换函数φ(·),η(·),ρ(·)可以是任意的。在这里,使用一个 Dense Block,并证明了它的图像 upscaling 任务的有效性。函数 ρ(·) 后面是一个 sigmoid 函数和一个 scale 项,以防止 exp(·) 函数引起的数值爆炸。注意,图 2 省略了 ρ 函数中的 exp(·)。
- Quantization
To save the output images of IRN as common image storage format such as RGB (8 bits for each R, G and B color channels), a quantization module is adopted which converts floating-point values of produced LR images to 8-bit unsigned int. We simply use rounding operation as the quantization module, store our output LR images by PNG format and use it in the upscaling procedure. There is one obstacle should be noted that the quantization module is nondifferentiable. To ensure that IRN can be optimized during training, we use Straight-Through Estimator [9] on the quantization module when calculating the gradients.
为了将 IRN 输出的图像保存为 RGB (每个R、G、B颜色通道8位) 等常用的图像存储格式,采用量化模块将产生的 LR 图像的浮点值转换为8位 unsigned int。本文简单地使用四舍五入运算作为量化模块,以 PNG 格式存储输出的 LR 图像,并在 upscaling 过程中使用它。需要注意的是,量子化模是不可微的。为了保证 IRN 在训练时能够得到优化,在计算梯度时,在量化模块上使用了Straight-Through Estimator。
Training Objectives
Based on Section 3.1, our approach for invertible downscaling constructs a model that specifies a correspondence between HR image x and LR image y, as well as a caseagnostic distribution p(z) of z. The goal of training is to drive these modeled relations and quantities to match our desiderata and HR image data {x (n)} N n=1. This includes three specific goals, as detailed below.
- LR Guidance
Downscaling 的图像与 Bicubic method 降维图像做 L1 或 L2 loss,如下公式所示:
- HR Reconstruction
虽然 ![]() 是可逆的,但当z不传输时,
是可逆的,但当z不传输时,![]() 和
和 ![]() 之间的对应关系就不可逆了。对于特定的缩小后的 LR 图像
之间的对应关系就不可逆了。对于特定的缩小后的 LR 图像 ![]() ,模型可以使用 case-agnostic
,模型可以使用 case-agnostic ![]() 中的任意
中的任意 ![]() 样本来恢复原始 HR 图像。
样本来恢复原始 HR 图像。
这个损失函数就是恢复的高分辨率图像与原高分辨率图像做 L1 或 L2 loss。
- Distribution Matching
distribution matching loss 的目的是鼓励网络捕捉输入 HR 图像数据的分布 ![]() ,使得模型重建的 HR 尽可能符合真实的 HR 数据分布。
,使得模型重建的 HR 尽可能符合真实的 HR 数据分布。
符号表示:
![]() : 输入 HR 图像;
: 输入 HR 图像;
![]() :从
:从 ![]() 变换得到的 LR 图像;
变换得到的 LR 图像;
![]() :随机采样信号;
:随机采样信号;
![]() :恢复的 HR 图像。
:恢复的 HR 图像。
则该损失函数表示为:
通过 JS 距离计算该损失函数:
Post 讲解
请参见博客 ECCV 2020 | 对损失信息进行建模,实现信号处理高保真还原