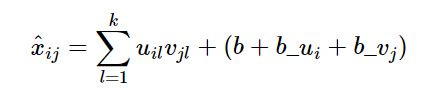矩阵补全（Matrix Completion）和缺失值预处理

前言

文章转载自：https://www.cnblogs.com/wuliytTaotao/p/10814770.html

1. 矩阵补全

矩阵补全（Matrix Completion），就是补上一个含缺失值矩阵的缺失部分。

矩阵补全可以通过矩阵分解（matrix factorization）将一个含缺失值的矩阵 $X$ 分解为两个（或多个）矩阵，然后这些分解后的矩阵相乘就可以得到原矩阵的近似 $X^{\prime }$，我们用这个近似矩阵 $X^{\prime }$ 的值来填补原矩阵 X 的缺失部分。

矩阵补全有很多方面的应用，如推荐系统、缺失值预处理。

除了 EM 算法、树模型，机器学习中的大多数算法都需要输入的数据是不含缺失值的。在 deep learning 模型中，通过梯度的计算公式就可以发现，如果 feature 中含有缺失值，那么梯度也会含缺失值，梯度也就未知了。对缺失值的处理是在模型训练开始前就应该完成的，故也称为预处理。

据缺失在实际场景中不可避免，对于一个包含 $n$ 个 samples，每个 sample 有 $m$ 个 features 的数据集 D，我们可以将该数据集 D 整理为一个 $n\ast m$ 的矩阵 $X$。

通过矩阵分解补全矩阵是一种处理缺失值的方式，但在介绍之前，先介绍一些简单常用的缺失值预处理方式。

2. 常用的缺失值预处理方式

2.1 不处理

不进行缺失值预处理，缺了就缺了，找一个对缺失值不敏感的算法（如“树模型”），直接训练。

2.2 剔除

对于矩阵 $X$ 中缺失值很多的行或列，直接剔除。

1列代表1个sample，1行代表一个feature。

缺失值较多的行，即一个 sample 的很多 features 都缺失了；缺失值较多的列，即大部分 samples 都没有该 feature。剔除这些 samples 或 features，而不是填充它们，避免引入过多的噪声。

当数据超级多时，我们甚至可以对含有缺失值的样本直接剔除，当剔除的比例不大时，这也完全可以接受。

2.3 填充

2.3.1 简单填充

在矩阵 $X$ 的每个缺失位置上填上一个数，来代替缺失值。填一个数也不能乱来，如果 feature 代表年龄，那么肯定要填正数；如果 feature 代表性别，那么填 0 或 1 更合适（0 代表男，1 代表女）。
一般有以下几种简单的填充值：（均值和众数都是在一个 feature 下计算，即在矩阵 $X$ 的每一列中计算均值和众数）

• 填 0
• 填 均值
• 填 众数
• 填 中位数

2.3.2 建模填充

这种方式通过观察缺失的 feature 和其它已有的 features 之间的联系，建立一个统计模型或者回归模型，然后然后预测缺失 feature 的值应该是什么。

用 EM 算法估计缺失值也可以归为这一类。

当然，常用的缺失值处理方式还有许多，这里就不再列举了。可以看看博客http://118.31.76.100:100/math/statics_topic/deal-na/

3. 利用矩阵分解补全缺失值

如果矩阵 $X$ 不含缺失值，那么矩阵分解可以将矩阵 $X$ 分解成两个矩阵 $U$ (大小 $m\times k$)、$V$ (大小 $m\times k$)，其中 $k<min\{m,n\}$，则：$$X=U{V}^T$$
因为 $k<min\{m,n\}$，所以 $rank(U)\le k$、$rank(V)\le k$，该矩阵分解又叫做低秩矩阵分解（low-rank matrix factorization）。

为什么 $k<min\{m,n\}$

• 在 samples 和 features 之间存在 $k$ 个关系，每个关系的具体含义不得而知，但如果 $k\ge min\{m,n\}$，那么意味着每个 sample 和 feature 之间可以构建一个的关系，而其它的 samples 或者 features 可以和该关系基本无关，体现在矩阵 U（或 V）中就是某一列仅有一个元素不为0，这是不合理的。（参考矩阵分解用在推荐系统方面的解释）
• 当 k 越大，计算量也会越大。

如果矩阵 $X$ 是完整的，那么矩阵分解 $X=U{V}^T$ 完全没问题，但现在 $X$ 中含了缺失值，故没有办法用线性代数的知识直接进行矩阵分解，我们需要一种近似的解法——梯度下降法

这个时候我们令 $X\approx \hat{X}=U{V}^T$，$\Vert X-\hat{X}{\Vert }_F^2$ 表示含缺失值的原矩阵 $X$ 和 还原后的近似矩阵 $\hat{X}$ 之间误差的平方（Square error），或者称之为 reconstruction error，当然 $\Vert X-\hat{X}{\Vert }_F^2$ 的计算只能在不含缺失值的项上。（∥⋅∥F 表示 Frobenius norm。）

文献中一般会将 reconstruction error $\Vert X-\hat{X}{\Vert }_F^2$ 记为 $\Vert {\mathcal{R}}_{\Omega }(X-\hat{X}){\Vert }_F^2$，其中$$[{\mathcal{R}}_{\Omega }(X-\hat{X}){]}_{ij}=\{\begin{array}{ll}{x}_{ij}-{\hat{x}}_{ij},& \text{if (i,j)ϵΩ}\\ 0,& \text{otherwise}\end{array}$$
其中$\Omega$ 表示非缺失值矩阵元素下标的集合。这里为了简便，直接使用 $\Vert X-\hat{X}{\Vert }_F^2$，知道只在不含缺失值的项上计算平方和即可。

我们的目标的是找到矩阵 $X$ 的近似矩阵 $\hat{X}$，通过 $\hat{X}$ 中对应的值来填充 $X$ 中缺失的部分。而想要找到 $\hat{X}$，就是要找到矩阵 $U$ 和 $V$。当然 $\hat{X}$ 要尽可能像 $X$，体现在函数上就是 $min\Vert X-\hat{X}{\Vert }_F^2$。

Loss function $J$ 为

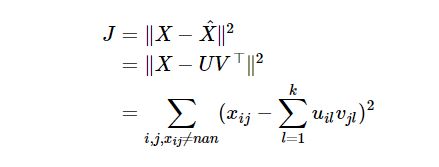
其中，$i,j$ 分别表示矩阵 $X$ 的行和列，要求 $x_{ij}\ne nan$，否则没有办法求最小值了。上式中，未知的就是 $u_{il}$,$v_{jl}$，也是我们想要求的。

随机初始化矩阵 $U$,$V$，loss function $J$ 就可以得到一个误差，基于该误差计算梯度，而想要更新 $U$,$V$，只需要按照梯度下降的公式来即可。

算法到这里其实就可以用了，但为了更加完美，可以考虑以下步骤，加入正则项和偏置。

3.1 加入正则项

加入正则项，保证矩阵 $U$,$V$ 中元素不要太大，此时 loss function $J$ 如下所示：

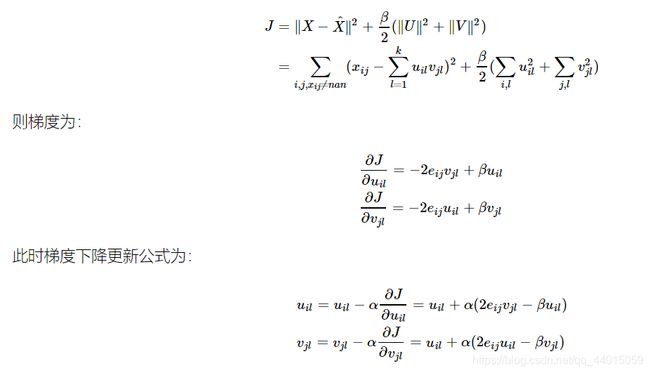
3.2 加入偏置

偏置可以理解为每个样本都有其特性，每个feature也有其特点，故可以加入 bias 来控制。bias 分为三种，第一种是矩阵 $X$ 整体的的 bias，记为 $b$，那么 $b=mean(X)$，即可以用矩阵 $X$ 中存在元素的均值来赋值；第二种是 sample 的 bias，记为 $b_{ui}$；第三种是 feature 的 bias，记为 $b_{vj}$。 则：