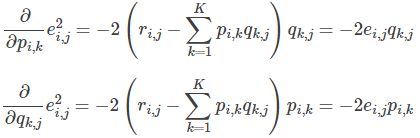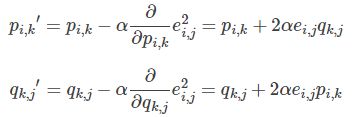梯度下降与矩阵分解

1.梯度下降

    梯度下降属于迭代法的一种，所谓迭代法就是不断用变量的旧值得到新值的方法。在求解损失函数最小值的时候，可以通过梯度下降法来一步步迭代求出最小化的损失函数和模型参数值。

    梯度：

              对于一元函数来说，梯度就是该函数的导数。即▽f(x)=f'(x)

              对于多元函数来说，梯度就是对多元函数的参数求偏导数，把求得的各个参数的偏导数以向量的形式写出来。比如函数f(x,y)，分别对x,y求偏导数，得到的的梯度就是(∂f/∂x, ∂f/∂y)T,简称grad f(x,y)或者▽f(x,y)。

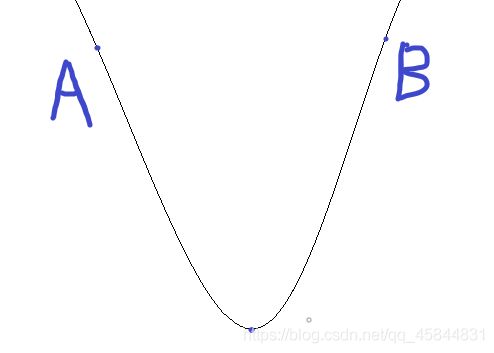
    在求极小值的时候，要向负梯度方向求最小值，以下图为例：

默认向上为y轴正方向，向右为x轴正方向

    在A点求最小值时要向梯度反方向，在B点求最小值时也是如此，梯度是在该点的导数。

   求解过程：

      1.设出两个较小的正数s,b       s代表步长，b代表非常小的常数阈值；

      2.求当前位置的偏导数：

       ▽f(x)=f'(x)；▽f(x,y)=(∂f/∂x, ∂f/∂y)T          (x=0....n)

      3.修改函数的参数值：

        X1=x-s*▽

       参数值为函数的梯度与步长的乘积的绝对值。

       4.如果修改后的参数值小于b,则此时的参数值就是求得最小值；否则回到步骤2，此时x=x-X0。

    一般情况下，梯度向量为0的时候就是一个极值点，此时梯度的幅值也为0。梯度下降算法迭代结束的条件是幅值接近0，故刚开始可以设置一个较小的阈值。

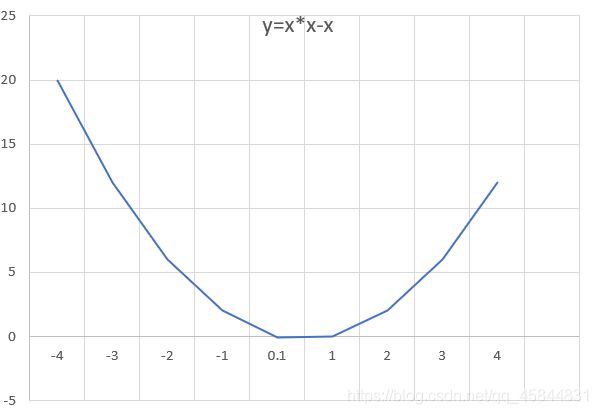
例：出发点设为-4利用梯度下降法求函数y=x*x-x的极小值

                         

def f(x):
    return 2*x-1
x=-4
s=0.9
b=0.01
while True:
    x1=f(x)*s
    if x1<0:
        x1=-x1
        x=x+x1
    else:
        x=x-x1
    if x1

 运行结果：

4.1
-2.38
2.8040000000000003
-1.3432000000000004
1.9745600000000003
-0.6796480000000003
1.4437184000000003
-0.2549747200000003
1.1039797760000003
0.01681617919999967
0.8865470566400003
0.19076235468799974
0.7473901162496003
0.3020879070003198
0.6583296743997442
0.37333626048020463
0.6013309916158363
0.418935206707331
0.5648518346341352
0.44811853229269183
0.5415051741658465
0.46679586066732276
0.5265633114661418
0.4787493508270866
0.5170005193383307
0.48639958452933546
0.5108803323765316
0.4912957340987747
0.5069634127209802
0.49442926982321583
0.5044565841414274
函数最小值 -0.24998728886898583

2.矩阵分解：

      矩阵分解就是把一个矩阵近似变成若干个小矩阵相乘的形式。个人感觉矩阵分解就是预测一些矩阵中没有的元素。

      应用矩阵分解思想解决评分矩阵中没有打分的元素，这种思想可以看做是有监督的机器学习。

      矩阵R可以近似表示为P与Q的乘积：R（m,n）≈ P(m,K)*Q(K,n)，为什么要说是近似表示呢，因为矩阵R中并不是所有的元素都有值，而分解后的矩阵P和Q是都有元素值的。K值是通过交叉验证法获得的最佳的值。，为了得到近似的R(m,n)，必须求出矩阵P和Q，如何求出这两个矩阵是关键问题。

      随机生成矩阵P和Q

      然后使用原始的评分矩阵与重新构建的评分矩阵之间的误差的平方作为损失函数，即：

      如果R(i,j)已知，则R(i,j)的误差平方和为：

　　            最终，需要求解所有的非“-”项的损失之和的最小值：

      之后使用梯度下降法获得修正的p和q分量：

•         求解损失函数的负梯度：

     

 

•        根据负梯度的方向更新变量：

     

 

       最后不停迭代直到算法最终收敛（直到sum(e^2) <=阈值）

import matplotlib.pyplot as plt
from math import pow
import numpy
def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
    Q=Q.T  # .T操作表示矩阵的转置
    result=[]
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    eij=R[i][j]-numpy.dot(P[i,:],Q[:,j]) # .dot(P,Q) 表示矩阵内积
                    for k in range(K):
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        eR=numpy.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
                    for k in range(K):
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
        result.append(e)
        if e<0.001:
            break
    return P,Q.T,result

if __name__ == '__main__':
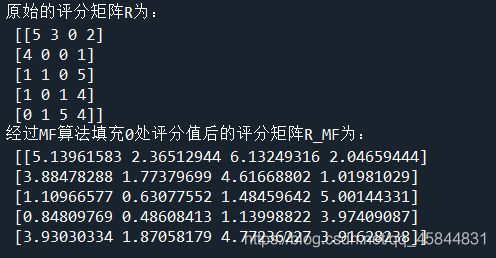
    R=[
        [5,3,0,2],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,1,4],
        [0,1,5,4]
    ]
    R=numpy.array(R)
    N=len(R)
    M=len(R[0])
    K=2

    P=numpy.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=numpy.random.rand(M,K) #随机生成一个 M行 K列的矩阵

    nP,nQ,result=matrix_factorization(R,P,Q,K)
    print("原始的评分矩阵R为：\n",R)
    R_MF=numpy.dot(nP,nQ.T)
    print("经过MF算法填充0处评分值后的评分矩阵R_MF为：\n",R_MF)

矩阵分解的方法和代码引用：https://www.cnblogs.com/shenxiaolin/p/8637794.html