MuZero：用学习模型规划玩转雅达利、围棋、国际象棋和日本将棋

Karen Simonyan,${}^{1\ast }$ Laurent Sifre,${}^{1,2\ast }$ Simon Schmitt,1 Arthur Guez,${}^{1\ast }$ Edward Lockhart,${}^1$ Demis Hassabis,${}^1$ Thore Graepel,${}^{1,2}$ Timothy Lillicrap,${}^1$ David Silver${}^{1,2\ast }$

${}^1$DeepMind, 6 Pancras Square, London N1C 4AG.
${}^2$University College London, Gower Street, London WC1E 6BT.
*These authors contributed equally to this work.

论文原文和补充资料（算法python伪代码）地址：

发表在《自然》的MuZero论文

MuZero论文预印版

DeepMind官方博客的MuZero介绍

MuZero算法的python伪代码

摘要

长期以来，构建具有规划能力的智能体（agents with planning capabilities）一直是人工智能研究的主要挑战之一。基于树的规划方法（Tree-based planning methods）在挑战性领域获得了巨大成功，例如国际象棋和围棋，这些领域都有一个完美的模拟器。然而，在现实世界中，动态控制/仿真环境往往是复杂且未知的。在这项工作中，我们提出了MuZero算法，该算法通过将基于树的搜索（tree-based search）与模型学习（learned model）相结合，在一系列极具挑战性的复杂视觉领域实现了超人的性能，而不需要了解环境的基本动力学。MuZero学习得到一个模型，迭代应用该模型，可以预测与规划最直接相关的数值：奖励、动作选择策略和价值函数。当对57种不同的Atari游戏（测试人工智能技术的标准视频游戏环境）进行评估时，我们的新算法与基于模型的规划方法对比，达到了新的技术水平。围棋、国际象棋和日本将棋上进行评估时，在对游戏规则一无所知的情况下，MuZero达到了与掌握游戏规则的AlphaZero算法相匹敌的超人性能。

1 介绍

基于前瞻搜索（lookahead search）的规划算法在人工智能领域取得了令人瞩目的成功。人类冠军已经在经典游戏中被击败，如在跳棋[34]、国际象棋[5]、围棋[38]和扑克[3,26]游戏中，规划算法在从物流[47]到化学合成[37]各领域应用中产生了现实影响。然而，这些规划算法都依赖于对环境动力学的了解（例如游戏规则或精确的模拟器），因此无法直接应用于机器人、工业控制或智能助手等实际领域。

基于模型的强化学习（RL）[42]首先要学习环境动力学模型，然后针对所学的模型进行规划来解决问题。通常，这些模型要么专注于重建真实的环境状态[8,16,24]，要么专注于完整观测序列[14,20]。然而，之前的这些工作[4,14,20]在复杂视觉领域，如Atari 2600游戏[2]中，远远没有达到最先进的水平。相反，最成功的方法是基于无模型RL[9,21,18]，它们直接在与环境的交互中估计最优策略和/或价值函数。然而，无模型算法在需要精确和复杂前瞻性的领域（如国际象棋和围棋）却远未达到最先进的水平。

在本文中，我们介绍了MuZero，一种新的基于模型的RL方法，它在Atari 2600游戏（复杂视觉领域）中实现了当今最先进的性能，同时在诸如国际象棋、日本将棋和围棋等精确规划任务中保持了超人的性能。AlphaZero[39]是强大的基于策略搜索的迭代算法，MuZero建立在此基础上，在训练过程中加入了一个学习模型（learned model）。MuZero还将AlphaZero扩展到更广泛的环境，包括单智能体域和中间时间步长的非零奖励。

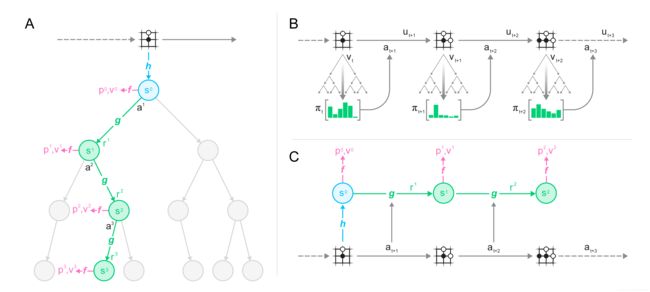
该算法的主要思想（如图1所示）是预测与规划直接相关的未来情况。模型接收观测结果（例如围棋棋盘或Atari游戏屏幕的图像）作为输入，并将其转换为隐藏状态。通过接收前一个隐藏状态和假想的下一个动作的循环过程迭代地更新隐藏状态。每一步，模型都会预测策略（如移动哪个棋子）、价值函数（如预测胜负）和即时奖励（移动棋子的得分）。对模型的训练是端到端的，其唯一目标是准确估计这三个重要的量，以便与改进的策略估计和搜索发现的价值以及观测到的奖励相匹配。对于隐藏状态，并不要求重建原始观测所需的全部信息，从而大大减少了模型必须维护和预测的信息量；也不需要匹配未知的真实环境状态或者对状态语义进行任何约束。相反，隐藏状态可以自由地以任何与预测当前和未来价值和策略相关的方式表征状态。形象一点说，智能体可以在其内部发明规则或动力学机制，从而实现最精确的规划。

2 前期工作

强化学习RL可分为两大类：基于模型（Model-based）的RL和无模型（Model-free）的RL[42]。基于模型的RL先构造出一个环境模型，作为中间环节。经典地，这个模型由一个马尔可夫决策过程MDP[31]来表示，它由两个部分组成：一个是状态转移模型，预测下一个状态，另一个是奖励模型，预测在状态转移期间的期望奖励。该模型通常以所选动作或临时抽象行为（如选项）作为条件[43]。一旦建立了模型，就可以直接应用MDP规划算法，如数值迭代[31]或蒙特卡罗树搜索MCTS[7]，来计算MDP的最优值或最优策略。在整体或部分可观测的环境中，算法必须首先构造模型应该预测的状态表征。表征的学习、模型的学习和规划三方之间是分裂的，这将造成潜在问题，智能体无法为达到有效规划的目标对表征或模型进行优化，因此，在规划期间，建模错误可能会特别严重。

基于模型的RL的一种常用方法是直接在像素级对观测流进行建模。有人设想深度随机模型可以缓解复合误差的问题[14,20]。但是，对像素级粒度进行规划，计算上很难处理大规模问题。其他方法建立的隐藏状态空间模型足以在像素级重建观测流[48,49]，或预测其未来的隐藏状态[13,11]，这有助于更有效的规划，但仍将大部分模型容量集中在潜在的无关细节上。这些先前的方法都没有能构建起一个模型促进复杂视觉领域（如Atari）的有效规划；结果是反而落后于优化的、无模型的方法，甚至在数据效率方面更是如此[45]。

最近开发了一种完全不同的基于模型的RL方法，专注在端到端预测价值函数[41]。这些方法的主要思想是构造一个抽象的MDP模型，使抽象的MDP中的规划等价于真实环境中的规划。这种等价是通过确保价值等价来实现的，即从同一真实状态开始，通过抽象的MDP的轨迹的累积奖励与真实环境中轨迹的累积奖励相匹配。

预测[41]首先引入了价值等价模型来预测价值（不实施动作）。尽管底层模型仍然采用MDP的形式，但它的转换模型不需要与环境中的真实状态相匹配。相反，MDP模型被视为深层神经网络的一个隐藏层。对展开的MDP进行训练，例如通过时间差分学习，使期望的累积奖励总和与实际环境的期望值相匹配。

价值等价模型随后扩展为优化价值（实施动作）。TreeQN[10]学习一个抽象的MDP模型，使得在该模型上的树搜索（由树结构的神经网络表征）逼近最优价值函数。价值迭代网络[44]学习一个局部MDP模型，使得该模型上的价值迭代（由卷积神经网络表征）逼近最优值函数。价值预测网络[28]可能是MuZero最失败的先驱：它们学习基于实际动作的MDP模型；展开的MDP经过训练，使得累积的奖励总和，以简单的前瞻搜索生成的实际动作序列为条件，与真实环境相匹配。与MuZero不同，没有策略预测，搜索只使用价值预测。

3 MuZero算法

图1：用学习模型进行规划、动作和训练。（A）MuZero使用模型进行规划。该模型由表征、动力学和预测三个相互连接的部分组成。给定一个先前的隐藏状态 $s^{k-1}$ 和一个候选动作 $a^k$ ，动力学函数 $g$ 就产生一个即时奖励 $r^k$ 和一个新的隐藏状态 $s^k$ 。隐藏状态 $s^k$ 经过预测函数 $f$，计算出策略 $p^k$ 和价值函数 $v^k$ 。过去的观测值（例如围棋棋盘或Atari屏幕）被传递给表征函数 $h$，以获得初始隐藏状态 $s^0$ 。（B）MuZero在环境中的动作。在每个时点 $t$ 进行MCTS，如A所述。一个动作 $a_{t+1}$ 是从搜索策略 ${\pi }_t$ 中采样得到的，该策略与根节点每个动作的访问计数成正比。环境接收到动作并生成新观测值 $o_{t+1}$ 和奖励 $u_{t+1}$ 。在回合结束时，将游戏轨迹保存在回放缓冲区。（C）MuZero训练它的模型。从回放缓冲区中抽取游戏轨迹。在初始推理阶段，表征函数 $h$ 根据抽取到的游戏轨迹的观测值 $o_1,...,o_t$ 作为输入。该模型循环展开为K步。每步k，动态函数 $g$ 收到前一步隐藏状态 $s^{k-1}$ 和实际动作 $a_{t+k}$ 作为输入。通过时间回溯（backpropagation-through-time），端到端地联合训练表征函数、动力学函数和预测函数的参数，以便能够预测三个数值：策略 $p^k\approx {\pi }_{t+k}$ 、价值函数 $v^k\approx z_{t+k}$ 和奖励 $r_{t+k}\approx u_{t+k}$ ，其中 $z_{t+k}$ 是回报：比如棋类游戏中的最终奖励，或者Atari中 $n$ 步的奖励。

我们现在更详细地描述MuZero算法。在每个时点 $t$ 做预测，预测步数为 $k=1...K$ ，用于预测的模型为 ${\mu }_{\theta }$ ，该模型的参数为 $\theta$ ，过去的观测值 $o_1,...,o_t$ 和未来的动作 $a_{t+1},...,a_{t+k}$ 为条件。该模型预测三个未来数值：策略 $p_t^k\approx \pi (a_{t+k+1}|o_1,...,o_t,a_{t+1},...,a_{t+k})$ 、价值函数 $v_t^k\approx \mathbb{E}[u_{t+k+1}+\gamma u_{t+k+2}+...|o_1,...,o_t,a_{t+1},...,a_{t+k}]$ ，以及即时奖励 $r_t^k\approx u_{t+k}$ ，其中 $u$ 是真实观测到的奖励，$\pi$ 是用于选择实际动作的策略，$\gamma$ 是环境的折扣系数。

在内部，每个时点 $t$ （为了简洁，以下省略了下标 $t$ ），模型由表征函数、动力学函数和预测函数的组合来表示。动力学函数 $r^k,s^k=g_{\theta }(s^{k-1},a^k)$ ，是一个循环过程，它在每个假想步 $k$ 计算即时奖励 $r^k$ 和内部状态 $s^k$ 。动力学函数反映了MDP模型结构，由给定状态和动作计算出预期奖励和状态转移[31]。然而，与基于模型的RL传统方法不同[42]，这种内部状态 $s^k$ 没有附加真实环境的语义，只是整个模型的隐藏状态，其唯一目的就是准确预测与未来相关的数值：策略、价值和奖励。在本文中，动力学函数被表示为确定过程，扩展为随机过程的工作留待以后进行。策略函数和价值函数，由预测函数 $p^k,v^k=f_{\theta }(s^k)$ ，根据内部状态 $s^k$ 计算得出，类似于AlphaZero的策略网络和价值网络的结合。“根”状态 $s^0$ 用于表征函数初始化，表征函数对过去观测值进行编码 $s^0=h_{\theta }(o_1,...,o_t)$ ；同样，除了帮助预测未来以外，它也没有任何特定语义。

给出这样一个模型，就有可能通过给定过去观测值 $o_1,...,o_t$ 搜索假想的未来游戏轨迹 $a^1,...,a^k$ 。比如，一个初级水平的搜索可能会简单选择 $k$ 步动作序列，使价值函数最大化。更一般地，我们可以将任何MDP规划算法应用于动力学函数生成的内部奖励和状态空间。特别地，我们使用了一种类似于AlphaZero搜索中采用的MCTS算法，该算法被推广到允许单智能体领域和有中间奖励的情况（参见附录的方法）。在每个中间节点，它利用了当前模型参数 $\theta$ 估计的策略、价值和奖励。MCTS算法最后输出一个推荐策略 ${\pi }_t$ 和估计价值 $v_t$ ，然后选择一个动作 $a_{t+1}\sim {\pi }_t$ 。

对模型的所有参数进行联合训练，以便在每个假想步 $k$ ，策略、价值和奖励都能与 $k$ 个时点过后实际观测到的目标值精确匹配。与AlphaZero类似，改进的策略目标值是通过MCTS搜索生成的；第一目标是最小化预测的策略 $p_t^k$ 与搜索的策略 ${\pi }_{t+k}$ 之间的误差。同样与AlphaZero类似，改进的价值目标值是通过玩游戏或MDP生成的；然而，与AlphaZero不同，我们允许带有折扣和中间奖励的长回合，方法是自举 $n$ 步进入未来，搜索值 $z_t=u_{t+1}+\gamma u_{t+2}+...+{\gamma }^{n-1}{u}_{t+n}+{\gamma }^n{v}_{t+n}$ 。在棋盘游戏中，最终结果 $\{lose,draw,win\}$ 被视为奖励 $u_t\in \{-1,0,+1\}$ ，出现在该回合的最后一步。具体来说，第二目标是最小化预测值 $v_t^k$ 与目标值 $z_{t+k}$ 之间的误差。奖励目标值仅为观察到的奖励；因此，第三目标是最小化预测奖励 $r_t^k$ 与观测到的奖励 $u_{t+k}$ 之间的误差。最后，还添加了 L2 正则化项，得到总体损失为：

$l_t(\theta )=\sum _{k=0}^K{l}^r(u_{t+k},r_t^k)+l^v(z_{t+k},v_t^k)+l^p({\pi }_{t+k},p_t^k)+c||\theta |{|}^2$

其中$l^r$、$l^v$和$l^p$分别是奖励、价值和策略的损失函数。补充图S2总结了MuZero算法进行规划、动作和学习的公式。

4 结果

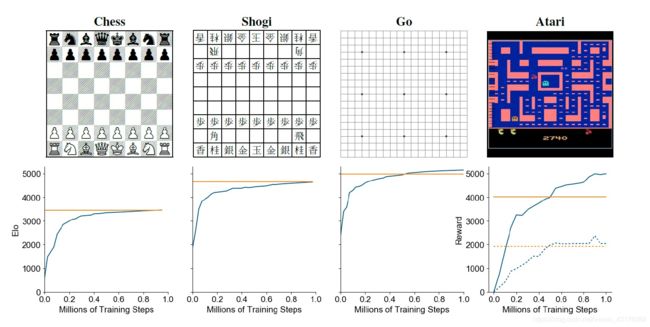
图2：在国际象棋、日本将棋、围棋和Atari的整个训练过程中对MuZero的评估。x轴是训练步数（单位为百万个）。对于国际象棋、围棋和围棋，y轴是Elo等级，这是通过对AlphaZero进行游戏建立的，两位玩家每一步使用800次模拟。MuZero的Elo由蓝线表示，AlphaZero的Elo由水平橙色线表示。对于Atari，y轴是所有57场比赛的人类标准化得分均值（实线）和中位数（虚线）。R2D2[21]的分数（该领域的最新技术，基于无模型RL）由水平橙色线表示。每4个时点用50次模拟来评估Atari的表现，然后重复所选择的动作4次，就像之前的工作一样[25]。

我们将MuZero算法应用于经典棋盘游戏围棋、国际象棋和日本将棋，作为具有挑战性的规划问题的基准，并应用于Atari学习环境中的所有57个游戏[2]，作为复杂视觉RL领域的基准。

在每种情况下，我们训练MuZero $K=5$个假想步骤。在棋盘游戏中进行了100万个小批量的2048大小的训练，在Atari进行了1024大小的训练。在训练和评估期间，MuZero对棋盘游戏中的每次搜索使用了800次模拟，对Atari中的每次搜索使用了50次模拟。表征函数使用与AlphaZero相同的卷积[23]和残差[15]结构，但是使用16个残差块而不是20个。动态函数使用与表征函数相同的体系结构，预测函数使用与AlphaZero相同的体系结构。所有网络都使用256个隐藏平面（有关详细信息，请参见附录）。

图2显示了每个游戏在整个训练过程中的表现。在围棋中，MuZero稍微超过了AlphaZero的性能，尽管在搜索树中每个节点使用较少的计算量（MuZero中每次计算16个残差块，而AlphaZero中为20个块）。这表明MuZero可能把其计算缓存在了搜索树中，并利用动力学模型带来的每个额外优势来获得对位置的更深入理解。

在Atari中，MuZero在57个游戏的街机学习环境中实现了最新的平均得分和中位数标准化得分，在57个游戏中的42个游戏中超过了之前最新的R2D2方法[21]（无模型方法），并且在所有游戏中都优于之前最好的基于模型的方法SimPLe[20]（见表S1）。

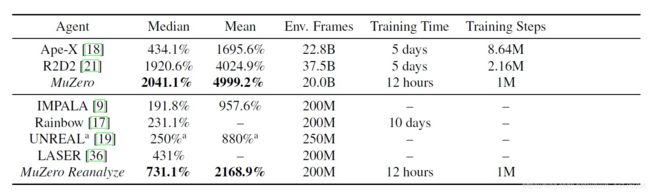
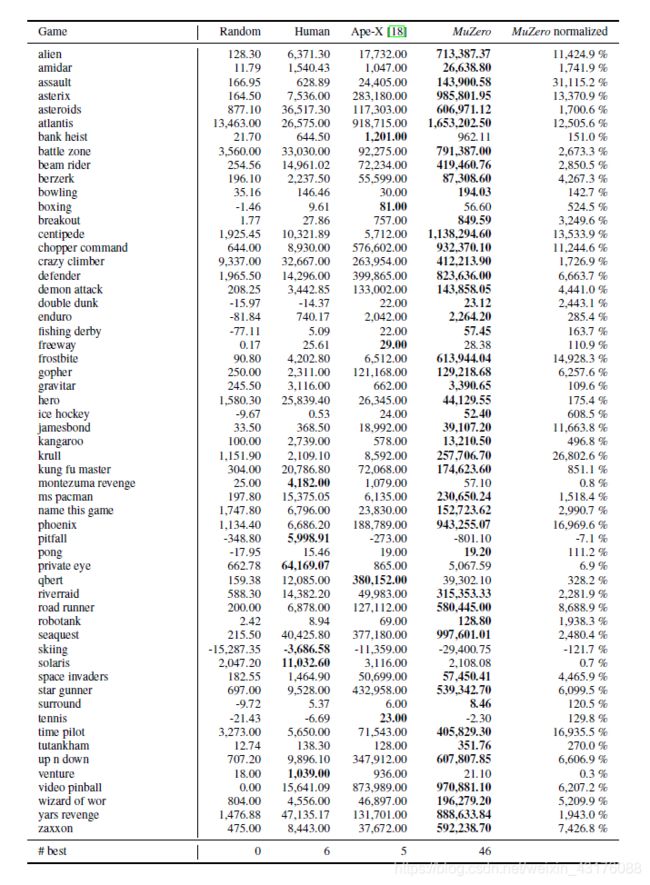
表1：MuZero与以前玩Atari的智能体比较。我们分别与在大（顶部）和小（底部）数据设置中训练的代理进行比较；除MuZero之外的所有代理都使用无模型RL技术。与人类测试者相比，给出了平均分和中位数。最佳结果以粗体突出显示。MuZero在这两种设置中都刷新了记录。${}^a$每个游戏都会调整一个超级参数。

我们还评估了MuZero的第二个版本，该版本经过了优化以提高样本效率。具体来说，它通过重运行使用新网络参数的MCTS来重分析旧的轨迹，以提供新的目标值（见附录H）。当应用于57款Atari游戏时，每个游戏使用2亿帧的经验，MuZero的重分析达到了731%的中位数标准化分数，而之前最先进的无模型方法IMPALA[9]、Rainbow[17]和LASER[36]分别为192%、231%和431%。

为了理解模型在MuZero中的作用，我们还进行了一些实验，重点是棋盘游戏的围棋和Atari游戏的Ms. Pacman。

首先，我们在围棋的规范规划问题中测试了规划的可伸缩性（图3 A）。我们比较了AlphaZero中使用完美模型的搜索性能和MuZero中使用学习模型的搜索性能。具体来说，通过比较不同思考时间的MCTS来评估完全训练的AlphaZero或MuZero。MuZero完全能与有完美模型的算法性能相匹敌，即使在进行搜索时（最多10秒的思考时间）比模型训练时（大约0.1秒的思考时间，另请参见图S3 A）大得多的情况下，也是如此。

我们还调查了所有Atari游戏规划的可伸缩性（见图3 B）。我们使用完全训练的MuZero对不同模拟次数的MCTS进行了比较。由于计划的改进远不如围棋中的显著，可能是因为更大的模型不精确性；性能随着搜索时间的增加略有改善，但在大约100次模拟中稳定下来。即使只进行一次模拟（即仅根据策略网络选择动作），MuZero的表现也很好，这表明在训练结束时，原始策略已经学会了内部化搜索的好处（另请参见图S3 B）。

接下来，我们测试对比了基于模型的学习算法与无模型学习算法（见图3 C）。我们将MuZero的训练目标（方程1）替换为无模型的Q-learning目标（如R2D2所用），将对偶值和策略头替换为单头表示Q-function $Q(\cdot |s^t)$ 。随后，我们在不使用任何搜索的情况下对新模型进行训练和评估。当在Ms. Pacman游戏上进行评估时，我们的无模型算法获得了与R2D2相同的结果，但R2D2的学习速度明显慢于MuZero，并收敛到一个更低的最终分数。我们推测MuZero基于搜索的策略改进步骤比Q-learning使用的高偏差、高方差目标提供了更强的学习信号。

为了更好地理解MuZero学习算法的本质，我们测量了MuZero的训练规模与训练期间使用的搜索量之间的关系。图3显示了Ms. Pacman游戏在整个训练过程中每次移动使用不同模拟计数的MCTS时的表现。令人惊讶的是，与之前的工作[1]相比，即使每个动作只有6个模拟（少于动作的数量），MuZero也学会了一个有效的策略并迅速改进。随着更多的模拟，性能大幅提升。对于每个单独迭代过程中策略改进的分析，请参见图S3 C和D。

5 结论

人工智能的许多突破要么基于高性能规划[5,38,39]，要么基于无模型强化学习方法[25,29,46]。在本文中，我们介绍了一种结合了两者优点的方法。我们的算法MuZero，既能匹敌超人表现的规划算法（他们擅长的领域是复杂逻辑棋类游戏，如国际象棋和围棋），也能超越最先进的无模型RL算法（他们擅长的领域是复杂视觉游戏Atari）。最关键的是，我们的方法不需要任何游戏规则或环境动力学的知识，为将强大的学习和规划方法应用到许多现实世界领域铺平了道路，而这些领域并不存在完美的模拟器。

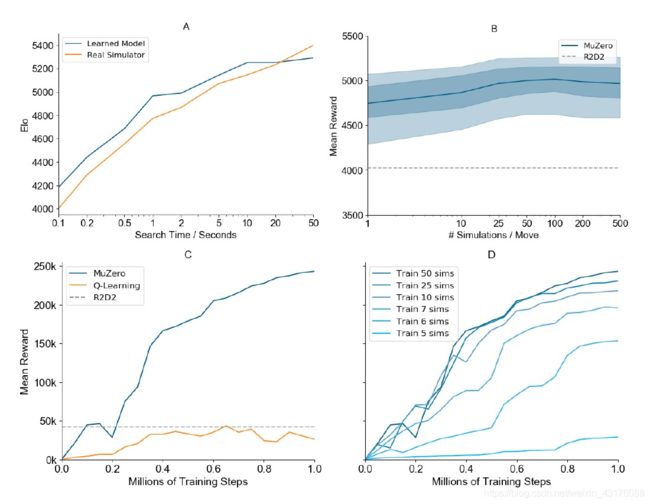
图3：MuZero在围棋（A）、所有57款Atari游戏（B）和Ms. Pacman游戏（C-D）上的评估。（A）缩放每次移动的搜索时间，比较学习模型和地面真实感模拟器。这两个网络的训练是每次搜索800次模拟，相当于每次搜索0.1秒。值得注意的是，学习模型能够很好地扩展到比训练时长两个数量级的搜索。（B） 用每次搜索的模拟次数缩放Atari中最终人类标准化平均得分。该网络每次搜索训练50次模拟。暗线表示平均得分，阴影区域表示第25至75百分位和第5至95百分位。学习模型的性能提高到100次模拟每搜索。除此之外，即使扩展到比训练时长得多的搜索，学习模型的性能仍然保持稳定，只是略有下降。这与Go（A）中更好的伸缩性形成了对比，可能是因为Atari中的模型比Go更不准确。（C）在MuZero框架下对Ms. Pacman进行基于MCTS的训练与Q学习的比较，保持网络规模和训练量不变。最先进的Q-学习算法R2D2作为基线显示。我们的Q-Learning实现与R2D2达到相同的最终分数，但与基于MCTS的训练相比，改进速度较慢，最终性能更低。（D） 不同的网络在每次移动中接受不同数量的模拟训练，但每次移动都要进行50次模拟评估。每次移动使用更多模拟训练的网络改进更快，与消融（B）一致，即每次移动使用更多模拟时策略改进更大。令人惊讶的是，MuZero可以有效地学习，即使训练时每次移动的模拟次数少于Ms. Pacman的8个可能动作的模拟次数。

6 致谢

Lorrayne Bennett、Oliver Smith和Chris Apps负责组织协助；Koray Kavukcuoglu负责审查论文；Thomas Anthony、Matthew Lai、Nenad Tomasev、Ulrich Paquet、Sumedh Ghaisas负责许多卓有成效的讨论；DeepMind团队的其他成员对他们的支持。

参考文献

[1] Kamyar Azizzadenesheli, Brandon Yang,Weitang Liu, Emma Brunskill, Zachary C. Lipton, and Animashree Anandkumar. Surprising negative results for generative adversarial tree search. CoRR, abs/1806.05780, 2018.
[2] Marc G Bellemare, Yavar Naddaf, Joel Veness, and Michael Bowling. The arcade learning environment: An evaluation platform for general agents. Journal of Artificial Intelligence Research, 47:253–279, 2013.
[3] Noam Brown and Tuomas Sandholm. Superhuman ai for heads-up no-limit poker: Libratus beats top professionals. Science, 359(6374):418–424, 2018.
[4] Lars Buesing, TheophaneWeber, Sebastien Racaniere, SM Eslami, Danilo Rezende, David P Reichert, Fabio Viola, Frederic Besse, Karol Gregor, Demis Hassabis, et al. Learning and querying fast generative models for reinforcement learning. arXiv preprint arXiv:1802.03006, 2018.
[5] Murray Campbell, A. Joseph Hoane, Jr., and Feng-hsiung Hsu. Deep blue. Artif. Intell., 134(1-2):57–83, January 2002.
[6] R. Coulom. Whole-history rating: A Bayesian rating system for players of time-varying strength. In International Conference on Computers and Games, pages 113–124, 2008.
[7] R´emi Coulom. Efficient selectivity and backup operators in monte-carlo tree search. In International conference on computers and games, pages 72–83. Springer, 2006.
[8] MP. Deisenroth and CE. Rasmussen. Pilco: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, pages 465–472. Omnipress, 2011.
[9] Lasse Espeholt, Hubert Soyer, Remi Munos, Karen Simonyan, Volodymir Mnih, Tom Ward, Yotam Doron, Vlad Firoiu, Tim Harley, Iain Dunning, et al. Impala: Scalable distributed deep-rl with importance weighted actor-learner architectures. In Proceedings of the International Conference on Machine Learning (ICML), 2018.
[10] Gregory Farquhar, Tim Rocktaeschel, Maximilian Igl, and Shimon Whiteson. TreeQN and ATreec: Differentiable tree planning for deep reinforcement learning. In International Conference on Learning Representations, 2018.
[11] Carles Gelada, Saurabh Kumar, Jacob Buckman, Ofir Nachum, and Marc G. Bellemare. DeepMDP: Learning continuous latent space models for representation learning. In Kamalika Chaudhuri and Ruslan Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pages 2170–2179, Long Beach, California, USA, 09–15 Jun 2019. PMLR.
[12] Cloud tpu. https://cloud.google.com/tpu/. Accessed: 2019.
[13] David Ha and J¨urgen Schmidhuber. Recurrent world models facilitate policy evolution. In Proceedings of the 32Nd International Conference on Neural Information Processing Systems, NIPS’18, pages 2455–2467, USA, 2018. Curran Associates Inc.
[14] Danijar Hafner, Timothy Lillicrap, Ian Fischer, Ruben Villegas, David Ha, Honglak Lee, and James Davidson. Learning latent dynamics for planning from pixels. arXiv preprint arXiv:1811.04551, 2018.
[15] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Identity mappings in deep residual networks. In 14th European Conference on Computer Vision, pages 630–645, 2016.
[16] Nicolas Heess, Greg Wayne, David Silver, Timothy Lillicrap, Yuval Tassa, and Tom Erez. Learning continuous control policies by stochastic value gradients. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2, NIPS’15, pages 2944–2952, Cambridge, MA, USA, 2015. MIT Press.
[17] Matteo Hessel, Joseph Modayil, Hado Van Hasselt, Tom Schaul, Georg Ostrovski,Will Dabney, Dan Horgan, Bilal Piot, Mohammad Azar, and David Silver. Rainbow: Combining improvements in deep reinforcement learning. In Thirty-Second AAAI Conference on Artificial Intelligence, 2018.
[18] Dan Horgan, John Quan, David Budden, Gabriel Barth-Maron, Matteo Hessel, Hado van Hasselt, and David Silver. Distributed prioritized experience replay. In International Conference on Learning Representations, 2018.
[19] Max Jaderberg, Volodymyr Mnih, Wojciech Marian Czarnecki, Tom Schaul, Joel Z Leibo, David Silver, and Koray Kavukcuoglu. Reinforcement learning with unsupervised auxiliary tasks. arXiv preprint arXiv:1611.05397, 2016.
[20] Lukasz Kaiser, Mohammad Babaeizadeh, Piotr Milos, Blazej Osinski, Roy H Campbell, Konrad Czechowski, Dumitru Erhan, Chelsea Finn, Piotr Kozakowski, Sergey Levine, et al. Model-based reinforcement learning for atari. arXiv preprint arXiv:1903.00374, 2019.
[21] Steven Kapturowski, Georg Ostrovski, Will Dabney, John Quan, and Remi Munos. Recurrent experience replay in distributed reinforcement learning. In International Conference on Learning Representations, 2019.
[22] Levente Kocsis and Csaba Szepesv´ari. Bandit based monte-carlo planning. In European conference on machine learning, pages 282–293. Springer, 2006.
[23] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
[24] Sergey Levine and Pieter Abbeel. Learning neural network policies with guided policy search under unknown dynamics. In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger, editors, Advances in Neural Information Processing Systems 27, pages 1071–1079. Curran Associates, Inc., 2014.
[25] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529, 2015.
[26] Matej Moravˇc´ık, Martin Schmid, Neil Burch, Viliam Lis`y, Dustin Morrill, Nolan Bard, Trevor Davis, Kevin Waugh, Michael Johanson, and Michael Bowling. Deepstack: Expert-level artificial intelligence in heads-up no-limit poker. Science, 356(6337):508–513, 2017.
[27] Arun Nair, Praveen Srinivasan, Sam Blackwell, Cagdas Alcicek, Rory Fearon, Alessandro De Maria, Vedavyas Panneershelvam, Mustafa Suleyman, Charles Beattie, Stig Petersen, Shane Legg, Volodymyr Mnih, Koray Kavukcuoglu, and David Silver. Massively parallel methods for deep reinforcement learning. CoRR, abs/1507.04296, 2015.
[28] Junhyuk Oh, Satinder Singh, and Honglak Lee. Value prediction network. In Advances in Neural Information Processing Systems, pages 6118–6128, 2017.
[29] OpenAI. Openai five. https://blog.openai.com/openai-five/, 2018.
[30] Tobias Pohlen, Bilal Piot, Todd Hester, Mohammad Gheshlaghi Azar, Dan Horgan, David Budden, Gabriel Barth-Maron, Hado van Hasselt, John Quan, Mel Veˇcer´ık, et al. Observe and look further: Achieving consistent performance on atari. arXiv preprint arXiv:1805.11593, 2018.
[31] Martin L. Puterman. Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley & Sons, Inc., New York, NY, USA, 1st edition, 1994.
[32] Christopher D Rosin. Multi-armed bandits with episode context. Annals of Mathematics and Artificial Intelligence, 61(3):203–230, 2011.
[33] Maarten PD Schadd, Mark HM Winands, H Jaap Van Den Herik, Guillaume MJ-B Chaslot, and Jos WHM Uiterwijk. Single-player monte-carlo tree search. In International Conference on Computers and Games, pages 1–12. Springer, 2008.
[34] Jonathan Schaeffer, Joseph Culberson, Norman Treloar, Brent Knight, Paul Lu, and Duane Szafron. A world championship caliber checkers program. Artificial Intelligence, 53(2-3):273–289, 1992.
[35] Tom Schaul, John Quan, Ioannis Antonoglou, and David Silver. Prioritized experience replay. In International Conference on Learning Representations, Puerto Rico, 2016.
[36] Simon Schmitt, Matteo Hessel, and Karen Simonyan. Off-policy actor-critic with shared experience replay. arXiv preprint arXiv:1909.11583, 2019.
[37] Marwin HS Segler, Mike Preuss, and Mark PWaller. Planning chemical syntheses with deep neural networks and symbolic ai. Nature, 555(7698):604, 2018.
[38] David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, and Demis Hassabis. Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587):484–489, January 2016.
[39] David Silver, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, Laurent Sifre, Dharshan Kumaran, Thore Graepel, et al. A general reinforcement learning algorithm that masters chess, shogi, and go through self-play. Science, 362(6419):1140–1144, 2018.
[40] David Silver, Julian Schrittwieser, Karen Simonyan, Ioannis Antonoglou, Aja Huang, Arthur Guez, Thomas Hubert, Lucas Baker, Matthew Lai, Adrian Bolton, Yutian Chen, Timothy Lillicrap, Fan Hui, Laurent Sifre, George van den Driessche, Thore Graepel, and Demis Hassabis. Mastering the game of go without human knowledge. Nature, 550:354–359, October 2017.
[41] David Silver, Hado van Hasselt, Matteo Hessel, Tom Schaul, Arthur Guez, Tim Harley, Gabriel Dulac-Arnold, David Reichert, Neil Rabinowitz, Andre Barreto, et al. The predictron: End-to-end learning and planning. In Proceedings of the 34th International Conference on Machine Learning-Volume 70, pages 3191–3199. JMLR. org, 2017.
[42] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction. The MIT Press, second edition, 2018.
[43] Richard S Sutton, Doina Precup, and Satinder Singh. Between mdps and semi-mdps: A framework for temporal abstraction in reinforcement learning. Artificial intelligence, 112(1-2):181–211, 1999.
[44] Aviv Tamar, YiWu, Garrett Thomas, Sergey Levine, and Pieter Abbeel. Value iteration networks. In Advances in Neural Information Processing Systems, pages 2154–2162, 2016.
[45] Hado van Hasselt, Matteo Hessel, and John Aslanides. When to use parametric models in reinforcement learning? arXiv preprint arXiv:1906.05243, 2019.
[46] Oriol Vinyals, Igor Babuschkin,WojciechMCzarnecki, Micha¨el Mathieu, Andrew Dudzik, Junyoung Chung, David H Choi, Richard Powell, Timo Ewalds, Petko Georgiev, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, pages 1–5, 2019.
[47] I Vlahavas and I Refanidis. Planning and scheduling. EETN, Greece, Tech. Rep, 2013.
[48] Niklas Wahlstr¨om, Thomas B. Sch¨on, and Marc Peter Deisenroth. From pixels to torques: Policy learning with deep dynamical models. CoRR, abs/1502.02251, 2015.
[49] Manuel Watter, Jost Tobias Springenberg, Joschka Boedecker, and Martin Riedmiller. Embed to control: A locally linear latent dynamics model for control from raw images. In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2, NIPS’15, pages 2746–2754, Cambridge, MA, USA, 2015. MIT Press.

补充材料

• MuZero算法的伪码描述。

• JSON格式的图2、图3、图S2、图S3、图S4和表1、表S1、表S2的数据。

补充材料可从arXiv提交文件的辅助文件部分获取。

附录A 与AlphaZero的比较

MuZero与AlphaGo Zero[40]和AlphaZero[39]相比，被设计得更通用。在AlphaGo-Zero和AlphaZero中，规划过程使用了两个独立的组件：模拟器，实现游戏规则，在遍历搜索树时用于更新游戏状态；神经网络，帮助预测模拟器生成的棋盘位置的相应策略和价值（见图1 A）。

具体来说，AlphaGo Zero和AlphaZero在三个地方使用到游戏规则的知识：（1）搜索树中的状态转移，（2）搜索树中每个节点上可用的动作，（3）在搜索树内的回合终点。在MuZero中，所有这些都被神经网络学习的单一隐式模型所取代（见图1 B）：

1）状态转移。AlphaZero拥有一个反映真实动力学过程的完美模拟器。相比之下，MuZero在其搜索中使用了一个学习的动力学模型。在该模型下，树中的每个节点都由一个对应的隐藏状态表示；通过向模型提供一个隐藏状态 $s_{k-1}$ 和一个动作 $a_k$ ，搜索算法可以转换到一个新节点 $s_k=g(s_{k-1},a_k)$。

2）可用动作。AlphaZero使用从模拟器获得的一组合法动作来mask网络在搜索树中任何地方产生的先验信息。MuZero只mask可以查询环境的搜索树根目录下的合法动作，但不在搜索树中执行任何mask。这是可能的，因为网络很快就学会了不去预测在它在训练轨迹上永远不会发生的动作。

3）终点节点。AlphaZero在表示终点状态的树节点停止搜索，并使用模拟器提供的终点值而不是网络生成的值。MuZero没有对终点节点进行特殊处理，总是使用网络预测的值。在树中，搜索可以经过一个终点节点——在这种情况下，期望网络总是预测相同的值。这是通过在训练期间将终点状态视为吸收状态来实现的。

此外，MuZero被设计成在一般的强化学习环境下运行：具有任意幅度折扣的中间奖励的单智能体领域。相比之下，AlphaGo-Zero和AlphaZero被设计用于两人游戏，没有折扣的终点奖励为 $\pm 1$。

附录B 搜索

我们现在描述MuZero使用的搜索算法。我们的方法基于带置信上限的蒙特卡罗树搜索，这是一种在单智能体领域中渐近收敛到最优策略的规划方法，在零和博弈中渐近收敛到极大极小值函数[22]。

搜索树的每个节点都与一个内部状态s相关联。对于 $s$ 的每个动作 $a$ ，都有一个边 $(s，a)$ ，这条边存储了一组统计信息 $\{N(s,a),Q(s,a),P(s,a),R(s,a),S(s,a)\}$，分别表示访问计数N、平均价值Q、策略P、奖励R和状态转移S。

与AlphaZero类似，搜索分为三个阶段，重复进行多次模拟。

选择（Selection）：每个模拟从内部根状态 $s^0$ 开始，当模拟到达叶节点 $s^l$ 时结束。对于模拟的每个假想步 $k=1,...,l$ ，利用在置信上限[32][39]上最大化的方法，根据存储的内部状态 $s^{k-1}$ 的统计信息选择动作 $a^k$ ，
$a^k=\underset{a}{\mathrm{argmax}}[Q(s,a)+P(s,a)\cdot \frac{\sqrt{{\sum }_{b}N(s,b)}}{1+N(s,a)}\cdot (c_1+log(\frac{{\sum }_{b}N(s,b)+c_2+1}{c_2}))]$ (2)

常数c1和c2用于控制相对于价值 $Q(s,a)$ ，先验的 $P(s,a)$ 对其影响。在我们的实验中，c1=1.25，c2=19652。

对于 $k<l$ ，下一个状态和奖励在状态转移和奖励表 $s^k=S(s^{k-1},a^k)$，$r^k=R(s^{k-1},a^k)$ 中查找。

扩展（Expansion）：在模拟的最后一个时间步 $l$，通过动力学函数 $r^l,s^l=g_{\theta }(s^{l-1},a^l）$ 计算奖励和状态，并将其存储在相应的表 $R(s^{l-1},a^l)=r^l$，$S(s^{l-1},a^l)=s^l$ 中。通过预测函数 $p^l,v^l=f_{\theta }(s^l)$ 计算策略和价值。一个新的节点，对应于状态 $s^l$ 被添加到搜索树中。来自新扩展节点的每条边 $(s^l,a)$ 被初始化为 $\{N(s^l,a)=0,Q(s^l,a)=0,P(s^l,a)=p^l\}$ 。请注意，搜索算法每次模拟最多分别调用一次动力学函数和预测函数；计算成本与AlphaZero中的阶数相同。

备份（Backup）：在模拟结束时，将更新沿轨迹的统计信息。将备份推广到环境可以给出中间奖励、且折扣不为1、价值估计为无界${}^3$的情况。对于 $k=l,...,0$ ，由价值函数 $v^l$ 自举，我们形成累积折扣奖励的 $l-k$ 步的估计，

$G^k=\sum _{\tau =0}^{l-1-k}{\gamma }^{\tau }{r}_{k+1+\tau }+{\gamma }^{l-k}{v}^l$ (3)

对于 $k=l,...,1$ ，我们更新模拟路径中每个边 $(s^{k-1},a^k)$ 的统计信息，如下所示，

$Q(s^{k-1},a^k):=\frac{N(s^{k-1},a^k)\cdot Q(s^{k-1},a^k)+G^k}{N(s^{k-1},a^k)+1}$

$N(s^{k-1},a^k):=N(s^{k-1},a^k)+1$ (4)

在两人零和对策中，假设价值函数在 $[0,1]$ 区间内有界。这种选择允许我们使用pUCT规则（公式2）将价值估计与概率结合起来。但是，由于在许多环境中，价值是无界的，因此有必要调整pUCT规则。一个简单的解决方案是使用在环境中可以观测到的最大分数来重新缩放价值或适当设置pUCT常数[33]。然而，这两种解决方案都是针对特定游戏的，需要向MuZero算法添加先验知识。为了避免这种情况，MuZero通过使用在该点之前在搜索树中观测到的最小值 - 最大值来计算标准化Q值用于估计 $\bar{Q}\in [0；1]$ 。当在选择（Selection）阶段到达一个节点时，该算法使用以下等式计算其边的标准化 $\bar{Q}$ 值，用于pUCT规则，公式如下：

$\bar{Q}(s^{k-1},a^k)=\frac{Q(s^{k-1},a^k)-mi{n}_{s,a\in Tree}Q(s,a)}{ma{x}_{s,a\in Tree}Q(s,a)-mi{n}_{s,a\in Tree}Q(s,a)}$ (5)

${}^3$在棋盘游戏中，假定折扣为1，没有中间奖励。

附录C 超参数

为了简单起见，我们优先使用与之前的工作中相同的体系结构选项和超参数。特别是，我们从AlphaZero的网络架构和搜索选择开始[39]。对于棋盘游戏，我们使用与AlphaZero相同的UCB常数、Dirichlet探索噪声和每次搜索800次模拟。

由于Atari中的分支因子要小得多，策略也简单得多，我们每次搜索只使用50次模拟来加速实验。如图3B所示，算法对这个选择不是很敏感。我们还使用与R2D2相同的折扣（0.997）和价值转换（见网络架构部分）[21]。

文中未提及的参数值请参考伪代码。

附录D 数据生成

为了生成训练数据，网络的最新检查点（每1000个训练步骤更新一次）使用与MCTS进行游戏。在棋盘游戏围棋，国际象棋和日本将棋中，每一步搜索800次模拟来选择一个动作；在Atari中，由于动作空间小得多，每一步50次模拟就足够了。

对于棋盘游戏，游戏一结束就送到训练任务。由于Atari游戏的长度要大得多（最多30分钟或108000帧），中间序列每200步发送一次。在棋盘游戏中，训练任务在内存重放缓冲区保存最近收到的100万个游戏；在Atari中，视觉观察较大，保存最近12.5万个长度为200的序列。

棋盘游戏领域，在产生经验的过程中，使用了与AlphaZero[39]中描述的相同的探索方案。Atari领域，则使用此方案的一个变体，在每个游戏期间，从访问计数分布中对动作进行采样，而不仅仅是前 $k$ 个动作。此外，访问计数分布使用温度参数 $T$ 参数化：

$p_{\alpha }=\frac{N(\alpha {)}^{1/T}}{{\sum }_{b}N(b{)}^{1/T}}$ (6)

$T$ 衰减为网络训练步数的函数。具体来说，前500k训练步骤的温度为1，接下来250k训练步骤的温度为0.5，其余250k训练步骤的温度为0.25。这确保了动作选择随着训练的进行而变得更加贪婪。

附录E 网络输入

表征函数

作为围棋、国际象棋和日本将棋表征函数输入的棋盘历史状态类似于AlphaZero[39]。在围棋和日本将棋中，我们将最后8个棋盘状态编码为与AlphaZero中的相同；在国际象棋中，我们将历史记录增加到最后100个棋盘状态，以便正确预测平局。

对于Atari，表征函数的输入包括分辨率为96x96的最后32个RGB帧以及导致每个帧的最后32个动作。我们对历史动作进行编码是因为与棋盘游戏不同，Atari中的动作不一定对观测有明显的影响。RGB帧被编码为每种颜色一个平面，分别为红色、绿色和蓝色重新缩放到范围 $[0,1]$ 。我们不执行其他规范化，白化或其他预处理的RGB输入。历史动作被编码为简单的偏置平面，按 $a/18$ 缩放（Atari中总共有18个动作）。

动力学函数

动力学函数的输入是表征函数生成的或之前应用动力学函数生成的隐藏状态，与动作表征级联。动作在与隐藏状态具有相同分辨率的平面中进行空间编码。在Atari中，这个分辨率是6x6（请参阅网络架构部分中的下采样说明），在棋盘游戏中，这个分辨率与棋盘大小相同（围棋是19x19，国际象棋是8x8，日本将棋是9x9）。

在围棋中，一个正常的动作（在棋盘落棋子）被编码为一个全零平面，其中一个在被玩棋子的位置。过程被编码为全零平面。

在国际象棋中，8个平面被用来编码动作。第一个one-hot平面编码棋子从哪个位置移动。接下来的两个平面对棋子移动到的位置进行编码：一个one-hot平面用于编码目标位置（如果在棋盘上），另一个二进制平面用于指示目标是否有效（在棋盘上）。这是必要的，因为为简单起见，我们的策略动作空间枚举了所有可能动作的超集，并非所有操作都是合法的，并且我们使用相同的动作空间进行策略预测和对动态函数输入进行编码。剩下的五个二进制平面用于表示提升的类型，如果有的话（皇后、骑士、主教、车、无）。

日本将棋的编码是相似的，总共有11个平面。我们使用前8个平面来指示棋子从何处移动-要么是棋盘位置（第一个one-hot平面）要么是七种囚徒类型中的一种（剩余的7个二进制平面）。接下来的两个平面用于对目标进行编码，就像在国际象棋中一样。剩下的二进制平面表示移动是否是升级。

在Atari中，一个动作被编码为一个one-hot向量，它被适当地平铺到平面中。

附录F 网络架构

预测函数 $p^k,v^k=f_{\theta }(s^k)$ 使用与AlphaZero相同的架构：一个或两个卷积层保留分辨率，但减少了平面的数量，然后用一个全连接层转换为输出大小。

对于Atari中的价值和奖励的预测，我们遵循[30]，使用一个可逆变换缩放目标值，可逆变换 $h(x)=sign(x)(\sqrt{|x|+1}-1)+\epsilon x$ ，其中ε=0.001（在我们所有的实验中）。然后，我们就可以对标量的价值和奖励目标值应用变换 $\varphi$ ，得到等价的分类表示。我们用一个大小为601的离散支持集，每个支持集包含 -300 和 300 之间的整数。在这种变换下，每个标量可以表示为其两个相邻支撑的线性组合，其原始值可以通过以下公式恢复： $x=x_{low}\ast p_{low}+x_{high}\ast p_{high}$ 。例如，3.7这个目标值可以表示为3支持度为0.3，4的支持度为0.7。网络输出的价值和奖励同样为601大小的softmax输出。在推演过程中，预测价值和奖励，要先计算它们softmax的期望值，然后再进行反向尺度变换。价值和奖励的缩放和转换在网络端是透明的，与算法其它部分无关。

表征函数和动力学函数都使用与AlphaZero相同的架构，但是使用16个而不是20个残差块[15]。我们使用3x3个内核和256个隐藏平面进行每个卷积。

对于Atari，观测值具有较大的空间分辨率，表征函数以stide为2的卷积序列开始，以降低空间分辨率。具体地说，从分辨率96x96和128个平面的输入观测开始（每个平面有3个彩色通道的32个历史帧，与广播到平面的相应32个动作相连），我们按如下方式进行下采样：

•1个卷积，步幅2和128个输出平面，输出分辨率48x48。
•2个残差块，128个平面
•1个卷积，步长2和256个输出平面，输出分辨率24x24。
•3个残差块，256个平面。
•步长为2的平均池，输出分辨率为12x12。
•3个残差块，256个平面。
•stide为2的平均池，输出分辨率为6x6。

所有操作的内核大小都是3x3。

对于动力学函数（始终以6x6的下采样分辨率运行），首先将动作编码为图像，然后与上一步的隐藏状态一起沿平面维度叠加。

附录G 训练

在训练过程中，MuZero网络展开为假想的K步，与MCTS自我对弈生成的轨迹中采样的序列对齐。序列是从回放缓冲区中保存的游戏中抽取的棋局，然后从该棋局展开 $K$ 步。在Atari中，样本是按照优先级从回放缓冲区[35]抽取的，优先级 $P(i)=\frac{P_i^{\alpha }}{{\sum }_k{P}_k^{\alpha }}$ ，其中 $pi=|v_i-z_i|$， $v$ 是搜索价值， $z$ 是观测到的n步回报。为了校正优先级采样引入的采样偏差，我们使用重要性采样率来衡量损失$w_i=(\frac{1}{N}\cdot \frac{1}{p(i)}{)}^{\beta }$。在我们所有的实验中，我们设置$\alpha =\beta =1$。对于棋盘类游戏，棋局是均匀抽样的。

序列上的每个观测点 $o_t$ 都有相应的MCTS策略 ${\pi }_t$ 、估计价值 $v_t$ 和环境奖励$u_t$。在每个展开的步骤k，网络相对该步骤的价值、策略和奖励目标值都有一个损失，求和得出MuZero网络的总损失（见公式1）。注意，在没有中间奖励的棋盘游戏中，我们忽略了奖励预测损失。对于棋盘游戏，我们直接自举到游戏结束，相当于预测最终结果；对于Atari，我们向未来自举 $n=10$ 步。

为了在不同的展开步骤中保持大致相似的梯度幅度，我们在两个不同的位置缩放梯度：

•我们对每个展开步骤的损失按 $1/K$ 进行缩放，其中 $K$ 是展开步数。这确保了无论展开多少步，总梯度都具有相似的大小。

•我们还将动力学函数开始处的梯度缩放 1/2 。这样可以确保应用于动力学函数的总梯度保持不变。

在本文报告的实验中，我们总是展开 $K=5$ 步。有关详细说明，请参见图1。

为了改进学习过程并绑定激活函数，我们还将隐藏状态扩展到与动作输入相同的范围$([0；1]):s_{scaled}=\frac{s-min(s)}{max(s)-min(s)}$。

所有实验都是使用第三代Google云TPUs进行的[12]。每一个棋盘游戏，我们用了16个TPU进行训练，1000个TPU进行自我对弈。在Atari的每一场游戏中，我们用了8个TPU进行训练，32个TPU进行自我对弈。在Atari游戏中TPU用的比较少是因为每次动作进行的模拟次数较少（50次而不是800次），并且动力学函数相对表征函数而言比较小。

附录H 重分析

为了提高MuZero的采样效率，我们引入了算法的第二个变体，MuZero重分析。MuZero重分析再次访问过去的时点，并使用最新的模型参数重新对其进行搜索，可能带来比原搜索更高质量的策略。在MuZero训练期间80%更新中，这个新策略被用作策略目标。进一步地，目标网络[25]，$v^{-}=f_{{\theta }^{-}}(s^0)$ ，基于最近参数 ${\theta }^{-}$ ，为价值函数提供了一个新的、稳定的n步自举目标，$z_t=u_{t+1}+\gamma u_{t+2}+...+{\gamma }^{n-1}{u}_{t+n}+{\gamma }^n{v}_{t+n}^{-}$ 。此外，还调整了其他几个超参数，主要为了增加样本重用和避免过度拟合价值函数。具体来说，每个状态抽取2.0个样本，而不是0.1；价值目标的权重降至0.25，而策略和奖励目标的权重为1.0；n步回报率降至 $n=5$ 步，而不是 $n=10$ 步。

附录I 评估

我们通过测量每个玩家的Elo等级来评估MuZero（图2）在棋类游戏中的相对强度。我们估计玩家a打败玩家b的概率，是通过逻辑函数 $p(a打败b)=(1+10^{(celo(e(b)-e(a)))}{)}^{-1}$，并通过贝叶斯逻辑回归来估计等级 $e()$ ，由BayesElo程序[6]使用标准常数 $c_{elo}=1/400$ 来计算。

Elo评分是根据训练期间MuZero和基线玩家（分别是Stockfish、Elmo或AlphaZero）迭代之间800次模拟每一步比赛的结果计算出来的。基线玩家每次移动的搜索时间相当于100毫秒。基线参与者的Elo评级基于公开的价值观[39]。

在Atari中，我们计算了每个游戏超过1000回合的平均奖励，每回合限制在标准的30分钟或108000帧[27]，除非另有说明，否则每次移动使用50个模拟。为了减轻Atari模拟器确定性的影响，我们采用了两种不同的评估策略：30个no-op的随机启动和人工启动。对于前者，在每回合开始时，在将控制权交给代理之前，向模拟器应用0到30个no-op动作的随机数。对于后者，在将控制权交给代理之前，从人类专家游戏中取样开始位置以初始化Atari模拟器[27]。

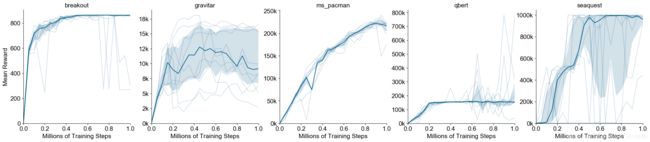
图S1：5个游戏在Atari中MuZero的重复性。y轴为总奖励，x轴训练步骤（单位为百万个）。暗线表示10次单独训练的中位数，浅线表示单独训练，阴影区域表示第25至75百分位。

表S1：Atari中30个随机no-op开始的单个游戏的MuZero评估。每场比赛的最佳结果以粗体突出显示。每回合最多30分钟的游戏时间（108k帧）。SimPLe仅对57场比赛中的36场进行了评估，不可用的结果用“-”表示。人类标准化得分计算为$s_{normalized}=\frac{s_{agent}-s_{random}}{s_{human}-s_{random}}$。

表S2：从人类起始位置对Atari中单个游戏的MuZero评估。每场比赛的最佳结果以粗体突出显示。每回合最多30分钟的游戏时间（108k帧）。

图S2：总结MuZero算法的方程式。这里，$\varphi (x)$ 是指通过相邻整数的线性组合表示实数 $x$，如“网络架构”一节中所述。

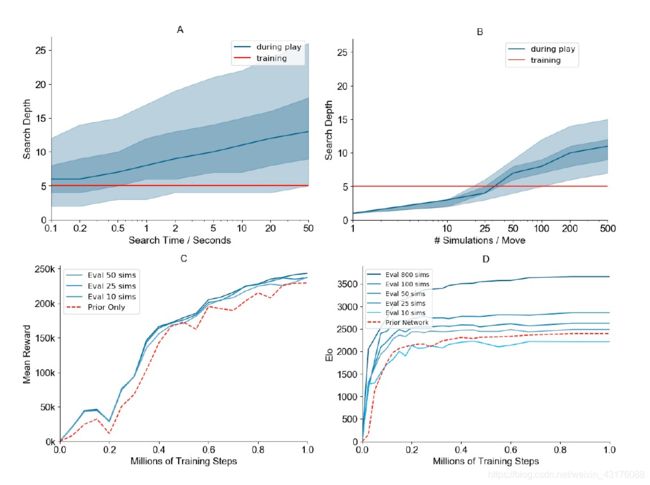
图S3：MuZero评估（A-B）和策略改进（C-D）的详细信息。（A-B）图3A-B中评估学习模型搜索树中评估深度的分布。如红线所示，对网络进行了5个假设步骤的训练。深蓝色线表示从根部开始的中位数深度，深色阴影区域显示第25至75百分位，浅色阴影区域显示第5至95百分位。（C） Ms.Pacman游戏的策略改进-单个网络在每次搜索50次模拟的情况下进行训练，并在每次搜索的不同模拟次数下进行评估，包括根据原始策略网络的argmax进行播放。搜索原始策略网络的策略改进效果在整个训练过程中清晰可见。有搜索和没有搜索的性能之间的这种一致性差距突出了MuZero利用的策略改进，通过不断地向改进的策略更新，有效地向最优策略前进。（D） 围棋中的策略改进-单个网络在每次搜索800次模拟的情况下进行训练，并在每次搜索的不同模拟次数下进行评估。在围棋中，长时间搜索的力量提升要比Ms.Pacman游戏大得多，而且在整个训练过程中都会持续，这与[40]中先前的结果一致。这表明，正如直觉所料，模型的好处在精确规划领域是最大的。

图S4：Atari中单个游戏的MuZero学习曲线。y轴为总奖励，x轴为训练步骤（单位为百万个）。曲线表示1000个评估游戏的平均得分，阴影区域表示标准差。