day4-聚类文章CONVEX BICLUSTERING

​1、本文将双聚类作为一个凸优化问题，提出了一种新的凸双聚类算法（COBRA）来迭代求解。COBRA输出的结果保留了聚类树图的简单可解释性和可视化，并且与现有技术相比还有几个关键优势：

• 稳定性和唯一性：COBRA为凸规划产生唯一的全局最小化，该最小化在数据中是连续的，这意味着COBRA总是将数据映射到单个双聚类分配，并且这个解决方案是稳定的；
• 简单性：COBRA采用单个调谐参数来控制双簇的数量；
• 数据自适应性：COBRA允许一个简单而有原则的数据自适应过程，用于选择涉及解决凸矩阵完成问题的调整参数。

2、L2范数是指向量各元素的平方和，然后求其平方根。（这个值也就是向量的模即向量的长度），由于向量旋转对于长度是不变的，所以根据L2范数的定义可知其大小与旋转变换无关，故L2范数具有旋转不变性。

3、优化问题的两大难题

• 局部最小值
• ill-condition病态问题，对于输入的细微改变会引起输出的巨大变化，说明系统不稳定。

4、条件数(condition-number)，是一个矩阵的稳定性或敏感的的度量，如果一个矩阵的条件数在1附近，那么它就是well-conditioned，如果远大于1，那么它就是ill-conditioned.

5、矩阵范数，假设$A\in R^{n\times n}$，其矩阵范数定义为：

$$||A||=\underset{x\ne 0}{\max }\frac{||Ax||}{||x||}$$

其中$||x||$是某一向量范数，下面举几个典型范数例子：
$l_1$矩阵范数（列和范数）
$$||A|{|}_1=\underset{j}{\max }||a_{.j}|{|}_1=\underset{j}{\max }\sum _{i=1}^n|a_{ij}|$$
​
$l_{\infty }$矩阵范数（行和范数）
$$||A|{|}_{\infty }=\underset{i}{\max }||a_{i.}|{|}_1=\underset{i}{\max }\sum _{j=1}^n|a_{ij}|$$

$l_2$矩阵范数（谱范数）
$$||A|{|}_2=({\lambda }_{A^{T}A}{)}^{\frac{1}{2}}$$
其中，${\lambda }_{A^{T}A}$表示$A^{T}A$的最大特征值，$a_{.j}$表示$A$的第$j$列，$a_{i.}$表示$A$的第$i$行。

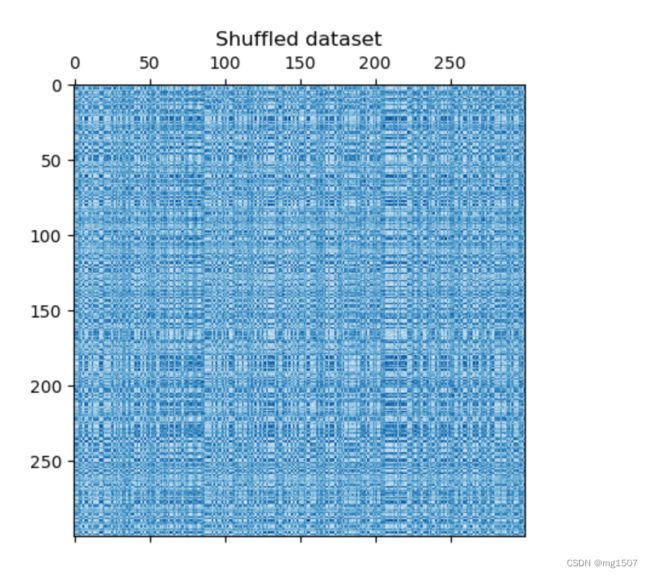
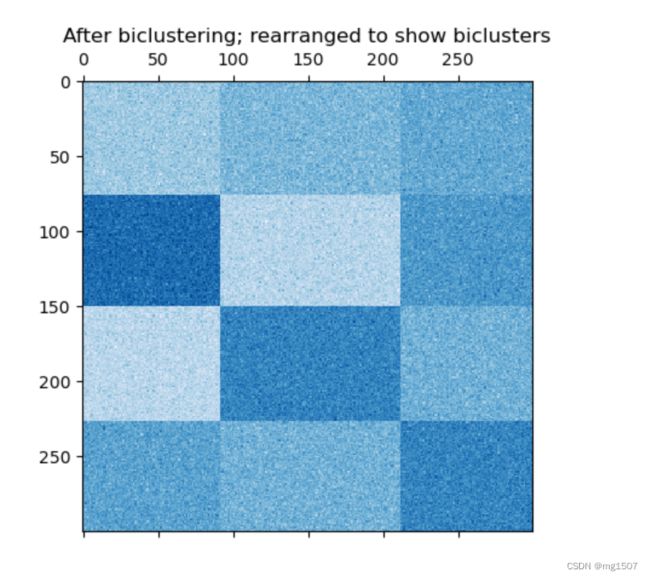
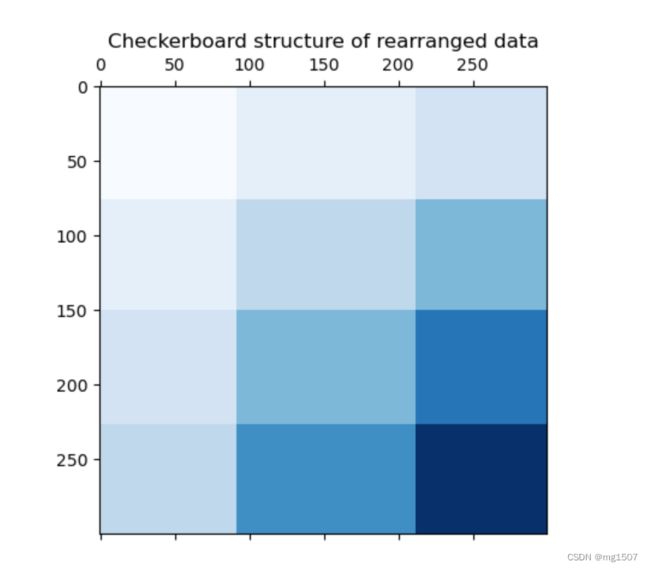
最后给个双聚类的例子来说明什么是双聚类，双聚类就是对行和列都进行聚类。

# Author: Kemal Eren 
# License: BSD 3 clause

import numpy as np
from matplotlib import pyplot as plt

from sklearn.datasets import make_checkerboard
from sklearn.cluster import SpectralBiclustering
from sklearn.metrics import consensus_score


n_clusters = (4, 3)
data, rows, columns = make_checkerboard(
    shape=(300, 300), n_clusters=n_clusters, noise=10, shuffle=False, random_state=0
)

plt.matshow(data, cmap=plt.cm.Blues)
plt.title("Original dataset")

# shuffle clusters
rng = np.random.RandomState(0)
row_idx = rng.permutation(data.shape[0])
col_idx = rng.permutation(data.shape[1])
data = data[row_idx][:, col_idx]

plt.matshow(data, cmap=plt.cm.Blues)
plt.title("Shuffled dataset")

model = SpectralBiclustering(n_clusters=n_clusters, method="log", random_state=0)
model.fit(data)
score = consensus_score(model.biclusters_, (rows[:, row_idx], columns[:, col_idx]))

print("consensus score: {:.1f}".format(score))

fit_data = data[np.argsort(model.row_labels_)]
fit_data = fit_data[:, np.argsort(model.column_labels_)]

plt.matshow(fit_data, cmap=plt.cm.Blues)
plt.title("After biclustering; rearranged to show biclusters")

plt.matshow(
    np.outer(np.sort(model.row_labels_) + 1, np.sort(model.column_labels_) + 1),
    cmap=plt.cm.Blues,
)
plt.title("Checkerboard structure of rearranged data")

# plt.show() # 该行不注释，在jupyter notebook中无法显示图片

活动地址：CSDN21天学习挑战赛