【自然语言处理】【知识图谱】知识图谱表示学习(二):TranSparse、PTransE、TransA、KG2E、TransG
【自然语言处理】【知识图谱】知识图谱表示学习(一):TransE、TransH、TransR、CTransR、TransD
【自然语言处理】【知识图谱】知识图谱表示学习(二):TranSparse、PTransE、TransA、KG2E、TransG
【自然语言处理】【知识图谱】知识图谱表示学习(三):SE、SME、LFM、RESCAL、HOLE
【自然语言处理】【知识图谱】知识图谱表示学习(四):【RotatE】基于复数空间关系旋转的知识图谱嵌入
【自然语言处理】【知识图谱】知识图谱表示学习(五):【PairRE】基于成对关系向量的知识图谱嵌入
一、符号
- 使用 G = ( E , R , T ) G=(E,R,T) G=(E,R,T)来表示完整的知识图谱,其中 E = { e 1 , e 2 , … , e ∣ E ∣ } E=\{e_1,e_2,\dots,e_{|E|}\} E={e1,e2,…,e∣E∣}表示实体集合, R = { r 1 , r 2 , … , r ∣ R ∣ } R=\{r_1,r_2,\dots,r_{|R|}\} R={r1,r2,…,r∣R∣}表示关系集合, T T T表示三元组集合, ∣ E ∣ |E| ∣E∣和 ∣ R ∣ |R| ∣R∣表示实体和关系的数量。
- 知识图谱以三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩的形式表示,其中 h ∈ E h\in E h∈E表示头实体, t ∈ E t\in E t∈E表示尾实体, r ∈ R r\in R r∈R表示 h h h和 t t t间的关系。
二、TranSparse
-
动机
TranSparse \text{TranSparse} TranSparse主要希望解决两个问题:
-
异质性
知识图谱中的关系粒度是不同的。一些复杂的关系可能会连接许多的实体对,但是简单的关系并不会。
-
不平衡
一些关系可能会连接很多的头实体,但连接的尾实体较少,反之亦然。
因此,如果考虑这些因素,而不仅仅是同等对待所有关系,那么就能得到进一步的改善。像 TransR \text{TransR} TransR这样的方法会为每个关系构建一个投影矩阵,但是每个关系的投影矩阵都具有相同的参数量,而没有考虑关系本身的复杂度问题。 TranSpare \text{TranSpare} TranSpare主要是解决这个问题,其主要假设是复杂关系应该比简单关键具有更多的参数量。一个关系的复杂度主要是依据关系连接的三元组或实体决定的。
-
-
方法
TranSpare \text{TranSpare} TranSpare主要有两个版本,分别是 TranSpare(share) \text{TranSpare(share)} TranSpare(share)和 TranSpare(separate) \text{TranSpare(separate)} TranSpare(separate)。
-
TranSpare(share) \text{TranSpare(share)} TranSpare(share)
类似于 TransR \text{TransR} TransR,该方法会为每个关系构建一个投影矩阵 M r ( θ r ) \textbf{M}_r(\theta_r) Mr(θr)。这个投影矩阵是稀疏的,其中稀疏度 θ r \theta_r θr主要依赖于关系 r r r连接的实体对数。设 N r N_r Nr是连接实体对的数量, N r ∗ N_r^* Nr∗表示所有 N r N_r Nr的最大数, θ m i n ( 0 ≤ θ m i n ≤ 1 ) \theta_{min}(0\leq\theta_{min}\leq 1) θmin(0≤θmin≤1)表示投影矩阵 M r \text{M}_r Mr最小稀疏度,那么关系 r r r的稀疏度定义为
θ r = 1 − ( 1 − θ m i n ) N r / N r ∗ \theta_r=1-(1-\theta_{min})N_r/N_r^* θr=1−(1−θmin)Nr/Nr∗
头尾实体会共享相同的稀疏矩阵 M r ( θ r ) \textbf{M}_r(\theta_r) Mr(θr)。评分函数为
E ( h , r , t ) = ∥ M r ( θ r ) h + r − M r ( θ r ) t ∥ \mathcal{E}(h,r,t)=\parallel \textbf{M}_r(\theta_r)\textbf{h}+\textbf{r}-\textbf{M}_r(\theta_r)\textbf{t}\parallel E(h,r,t)=∥Mr(θr)h+r−Mr(θr)t∥ -
TranSpare(separate) \text{TranSpare(separate)} TranSpare(separate)
不同于 TranSpare(share) \text{TranSpare(share)} TranSpare(share), TranSpare(separate) \text{TranSpare(separate)} TranSpare(separate)会为头尾实体构建两个不同的稀疏矩阵 M r h ( θ r h ) \textbf{M}_{rh}(\theta_{rh}) Mrh(θrh)和 M r t ( θ r t ) \textbf{M}_{rt}(\theta_{rt}) Mrt(θrt)。稀疏度 θ r h \theta_{rh} θrh和 θ r t \theta_{rt} θrt分别依赖关系 r r r连接头实体和尾实体的数量。令 N r h N_{rh} Nrh和 N r t N_{rt} Nrt表示头尾实体的数量, N r h ∗ N_{rh}^* Nrh∗和 N r t ∗ N_{rt}^* Nrt∗表示 N r h N_{rh} Nrh和 N r t N_{rt} Nrt的最大值, θ m i n \theta_{min} θmin仍然被设为投影矩阵的最小稀疏度,则有
θ r h = 1 − ( 1 − θ m i n ) N r h / N r h ∗ , θ r t = 1 − ( 1 − θ m i n ) N r t / N r t ∗ \theta_{rh}=1-(1-\theta_{min})N_{rh}/N_{rh}^*,\quad\theta_{rt}=1-(1-\theta_{min})N_{rt}/N_{rt}^* θrh=1−(1−θmin)Nrh/Nrh∗,θrt=1−(1−θmin)Nrt/Nrt∗
评分函数为
E ( h , r , t ) = ∥ M r h ( θ r h ) h + r − M r t ( θ r t ) t ∥ \mathcal{E}(h,r,t)=\parallel \textbf{M}_{rh}(\theta_{rh})\textbf{h}+\textbf{r}-\textbf{M}_{rt}(\theta_{rt})\textbf{t}\parallel E(h,r,t)=∥Mrh(θrh)h+r−Mrt(θrt)t∥
-
三、PTransE
-
动机
TransE \text{TransE} TransE模型仅考虑一跳关系,忽略了整个知识图谱中丰富的全局信息。在模型中考虑多跳关系是一种利用全局信息的可行方法。举例来说,考虑多跳关系
⟨ The forbidden city,locate_in,Beijing ⟩ → ⟨ Beijing,captial_of,China ⟩ \langle\text{The forbidden city,locate\_in,Beijing}\rangle\rightarrow\langle\text{Beijing,captial\_of,China}\rangle ⟨The forbidden city,locate_in,Beijing⟩→⟨Beijing,captial_of,China⟩
那么可以推断出三元组 ⟨ The forbidden city,locate_in,China ⟩ \langle\text{The forbidden city,locate\_in,China}\rangle ⟨The forbidden city,locate_in,China⟩。编码多跳关系主要面临两个挑战。
- 如何从知识图谱海量的候选路径中挑选出可靠且具有真实意义的路径?
- 在关系路径中存在着复合语义问题,那么如何建模这些有意义的关系路径?
-
方法
-
PCRA \text{PCRA} PCRA
PTransE \text{PTransE} PTransE的目标是解决多跳关系路径问题。为了能够挑选出有意义的关系路径,作者提出了一种称为 PCRA(Path-Constraint Resource Allocation) \text{PCRA(Path-Constraint Resource Allocation)} PCRA(Path-Constraint Resource Allocation)的算法来判断一条路径的可靠性。
假设头实体 h h h中存在着一些信息,这些信息沿着一些路径最终传递至尾实体 t t t。那么算法 PCRA \text{PCRA} PCRA的基础假设是:头实体中的信息经由路径 l l l传递至尾实体越多,那么路径 l l l就越可靠。
正式来说,令 l = ( r 1 , … , r l ) l=(r_1,\dots,r_l) l=(r1,…,rl)为 h h h和 t t t之间的一条具体路径。那么信息从 h h h传递至 t t t的路径可以表示为
S 0 / h → r 1 S 1 → r 2 … → r l S l / t S_0/h\mathop{\rightarrow}^{r_1}S_1\mathop{\rightarrow}^{r_2}\dots\mathop{\rightarrow}^{r_l}S_l/t S0/h→r1S1→r2…→rlSl/t
对于给定的一个实体 m ∈ S i m\in S_i m∈Si,那么传递至 m m m的信息量定义为
R l ( m ) = ∑ n ∈ S i − 1 ( ⋅ , m ) 1 ∣ S i ( n , ⋅ ) ∣ R l ( n ) R_l(m)=\sum_{n\in S_{i-1}(\cdot,m)}\frac{1}{|S_i(n,\cdot)|}R_l(n) Rl(m)=n∈Si−1(⋅,m)∑∣Si(n,⋅)∣1Rl(n)
其中, S i − 1 ( ⋅ , m ) S_{i-1}(\cdot,m) Si−1(⋅,m)是实体 m m m沿着关系 r i r_i ri的所有直接前继节点,这些前继节点位于 S i − 1 S_{i-1} Si−1; S i ( n , ⋅ ) S_i(n,\cdot) Si(n,⋅)表示节点 n ∈ S i − 1 n\in S_{i-1} n∈Si−1的所有后继节点。最终,传统至尾实体 t t t的信息量为 R l ( t ) R_l(t) Rl(t),该值用于衡量三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩是否可靠。 -
PTransE \text{PTransE} PTransE
在挑选出可靠的路径后,就需要为多跳路径进行有意义的建模。 PTransE \text{PTransE} PTransE提出了三种方式建模多跳路径,分别是:加、乘和递归神经网络,从而获得了路径 l = ( r 1 , … , r l ) \mathcal{l}=(r_1,\dots,r_l) l=(r1,…,rl)的向量表示 l \textbf{l} l。
最终路径三元组 ⟨ h , l , t ⟩ \langle h,l,t\rangle ⟨h,l,t⟩定义为
E ( h , l , t ) = ∥ l-(t-h) ∥ ≈ ∥ l-r ∥ = E ( l , r ) \mathcal{E}(h,l,t)=\parallel\textbf{l-(t-h)}\parallel\approx\parallel\textbf{l-r}\parallel=\mathcal{E}(l,r) E(h,l,t)=∥l-(t-h)∥≈∥l-r∥=E(l,r)
其中, r r r表示实体 h h h和 t t t的真实关系。PTransE \text{PTransE} PTransE在建模多跳路径的同时,也需要像 TransE \text{TransE} TransE那么满足 r ≈ t-h \textbf{r}\approx\textbf{t-h} r≈t-h,因此 PTransE \text{PTransE} PTransE也需要直接利用 r \textbf{r} r进行训练。 PTransE \text{PTransE} PTransE的优化目标为
L = ∑ ( h , r , t ) ∈ S [ L ( h , r , t ) + 1 Z ∑ l ∈ P ( h , t ) R ( l ∣ h , t ) L ( l , r ) ] \mathcal{L}=\sum_{(h,r,t)\in S}[\mathcal{L}(h,r,t)+\frac{1}{Z}\sum_{l\in P(h,t)}R(l|h,t)\mathcal{L}(l,r)] L=(h,r,t)∈S∑[L(h,r,t)+Z1l∈P(h,t)∑R(l∣h,t)L(l,r)]
其中, L ( h , r , t ) \mathcal{L}(h,r,t) L(h,r,t)就是基于评分函数 E ( h , r , t ) \mathcal{E}(h,r,t) E(h,r,t)的损失函数, L ( l , r ) \mathcal{L}(l,r) L(l,r)则是基于评分函数 E ( l , r ) \mathcal{E}(l,r) E(l,r)的损失函数, R ( l ∣ h , t ) R(l|h,t) R(l∣h,t)是路径三元组 ( h , l , t ) (h,l,t) (h,l,t)中路径 l l l的可靠性。
-
四、TransA
-
动机
TransA \text{TransA} TransA解决了 TransE \text{TransE} TransE及其相关扩展模型的几个问题:
- TransE \text{TransE} TransE及其扩展模型中仅考虑了欧式距离,这意味着缺少灵活性;
- 当前的这些方法会同等对待语义向量空间中的每个维度,这可能会在计算相似度的时候带来误差;
-
方法
TransA \text{TransA} TransA将欧式距离换成了马氏距离,其具有更好的适应性和灵活性。评分函数定义为
E ( h , r , t ) = ( ∣ h+r-t ∣ ) ⊤ W r ( ∣ h+r-t ∣ ) \mathcal{E}(h,r,t)=(|\textbf{h+r-t}|)^\top\textbf{W}_r(|\textbf{h+r-t}|) E(h,r,t)=(∣h+r-t∣)⊤Wr(∣h+r-t∣)
其中, W r \textbf{W}_r Wr是针对具体关系的非负、对称的自适应矩阵。其中, ∣ h+r-t ∣ |\textbf{h+r-t}| ∣h+r-t∣是非负向量,每个维度都是翻译操作的决定值。
( ∣ h+r-t ∣ ) = △ ( ∣ h 1 + r 1 − t 1 ∣ , ∣ h 2 + r 2 − t 2 ∣ , … , ∣ h n + r n − t n ∣ ) (|\textbf{h+r-t}|)\mathop{=}^\triangle(|h_1+r_1-t_1|,|h_2+r_2-t_2|,\dots,|h_n+r_n-t_n|) (∣h+r-t∣)=△(∣h1+r1−t1∣,∣h2+r2−t2∣,…,∣hn+rn−tn∣)
五、KG2E
-
动机
目前这些基于翻译的模型通常会将实体和关系看作是低维语义空间中的向量。但是,知识图谱中的实体和关系粒度是不同的。因此,被用来区分正三元组和负三元组的基于边界的损失函数应该更加灵活,从而适应知识图谱的灵活性。
-
方法
为了解决上面的问题, KG2E \text{KG2E} KG2E在知识图谱表示中引入了多维高斯分布。 KG2E \text{KG2E} KG2E将每个实体和关系表示成一个高斯分布。具体来说,高斯分布中的均值向量是实体(关系)的中心位置,协方差矩阵则是表示不确定性。为了能够学习到实体和关系的高斯分布, KG2E \text{KG2E} KG2E仍然使用 TransE \text{TransE} TransE中的评分函数。对于三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩,实体和关系的高斯分布定义为
h ∼ N ( u h , Σ h ) , t ∼ N ( u t , Σ t ) , r ∼ N ( u r , Σ r ) \textbf{h}\sim\mathcal{N}(u_h,\Sigma_h),\quad\textbf{t}\sim\mathcal{N}(u_t,\Sigma_t),\quad\textbf{r}\sim\mathcal{N}(u_r,\Sigma_r) h∼N(uh,Σh),t∼N(ut,Σt),r∼N(ur,Σr)
考虑到效率问题,协方差矩阵是对角阵。 KG2E \text{KG2E} KG2E假设头结点和尾结点是独立的,那么翻译操作就定义为h-t就定义为
h-t = e ∼ N ( u h − u t , Σ h + Σ t ) \textbf{h-t}=\textbf{e}\sim\mathcal{N}(u_h-u_t,\Sigma_h+\Sigma_t) h-t=e∼N(uh−ut,Σh+Σt)
为了衡量 e \textbf{e} e和 r \textbf{r} r的不相似性, KG2E \text{KG2E} KG2E提出了2种方法来同时考虑非对称相似度和对称相似度。
- 非对称关系是 e \textbf{e} e和 r \textbf{r} r的KL散度,那么评分函数定义为
E ( h , r , t ) = D K L ( e||r ) = ∫ x ∈ R k e N ( x ; u r , Σ r ) l o g N ( x ; u e , Σ e ) N ( x ; u r , Σ r ) d x = 1 2 { t r ( Σ r − 1 Σ r ) + ( u r − u e ) ⊤ Σ r − 1 ( u r − u e ) − l o g d e t ( Σ e ) d e t ( Σ r ) − k e } \begin{aligned} \mathcal{E}(h,r,t)&=D_{KL}(\textbf{e||r}) \\ &=\int_{x\in R^{k_e}}\mathcal{N}(x;u_r,\Sigma_r)log\frac{\mathcal{N}(x;u_e,\Sigma_e)}{\mathcal{N}(x;u_r,\Sigma_r)}dx \\ &=\frac{1}{2}\Big\{tr(\Sigma_r^{-1}\Sigma_r)+(u_r-u_e)^\top\Sigma_r^{-1}(u_r-u_e)-log\frac{det(\Sigma_e)}{det(\Sigma_r)}-k_e\Big\} \end{aligned} E(h,r,t)=DKL(e||r)=∫x∈RkeN(x;ur,Σr)logN(x;ur,Σr)N(x;ue,Σe)dx=21{tr(Σr−1Σr)+(ur−ue)⊤Σr−1(ur−ue)−logdet(Σr)det(Σe)−ke}
其中, t r ( Σ ) tr(\Sigma) tr(Σ)是矩阵 Σ \Sigma Σ的迹, Σ − 1 \Sigma^{-1} Σ−1是逆矩阵。
- 对称关系是基于期望似然或者概率乘积核。 KG2E \text{KG2E} KG2E使用 P e P_e Pe和 P r P_r Pr的内积来衡量相似性,评分函数为
E ( h , r , t ) = ∫ x ∈ R k e N ( x ; u e , Σ e ) N ( x ; u r , Σ r ) d x = l o g N ( 0 ; u e − u r , Σ e + Σ r ) = 1 2 { ( u e − u r ) ⊤ ( Σ e + Σ r ) − 1 ( u e − u r ) + l o g d e t ( Σ e + Σ r ) + k e l o g ( 2 π ) } \begin{aligned} \mathcal{E}(h,r,t)&=\int_{x\in R^{k_e}}\mathcal{N}(x;u_e,\Sigma_e)\mathcal{N}(x;u_r,\Sigma_r)dx \\ &=log\mathcal{N}(0;u_e-u_r,\Sigma_e+\Sigma_r) \\ &=\frac{1}{2}\Big\{(u_e-u_r)^\top(\Sigma_e+\Sigma_r)^{-1}(u_e-u_r)+log\;det(\Sigma_e+\Sigma_r)+k_elog(2\pi)\Big\} \end{aligned} E(h,r,t)=∫x∈RkeN(x;ue,Σe)N(x;ur,Σr)dx=logN(0;ue−ur,Σe+Σr)=21{(ue−ur)⊤(Σe+Σr)−1(ue−ur)+logdet(Σe+Σr)+kelog(2π)}
KG2E \text{KG2E} KG2E的优化目标与 TransE \text{TransE} TransE相似。
六、TransG
-
动机
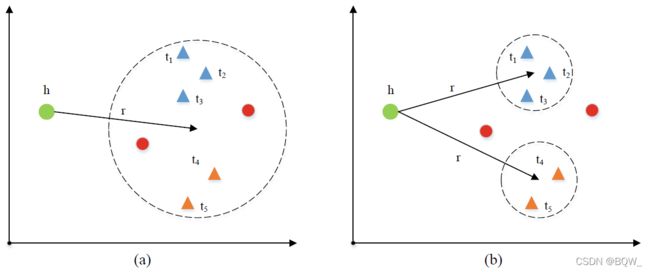
知识图谱中存在着一些像 location_contains \text{location\_contains} location_contains或者 has_part \text{has\_part} has_part这样复杂的、包括子含义的关系。这种复杂的关系可以是一些其他关系的组合,因此也可以被分割成几个更精确的关系。为了解决这种问题, CTransR \text{CTransR} CTransR通过为每个关系 r r r的实体对 ( h , t ) (h,t) (h,t)进行聚类。 TransG \text{TransG} TransG通过引入生成模型来更优雅的解决这个问题。
-
方法
TransG \text{TransG} TransG假设不同的语义组件嵌入向量遵循高斯混合模型。整个生成过程如下:
- 对于每个实体 e ∈ E e\in E e∈E, TransG \text{TransG} TransG设定了一个标准正态分布 u e ∼ N ( 0,I ) \textbf{u}_e\sim\mathcal{N}(\textbf{0,I}) ue∼N(0,I);
- 对于任一三元组 ⟨ h , r , t ⟩ \langle h,r,t \rangle ⟨h,r,t⟩, TransG \text{TransG} TransG使用 CRP(Chinese Restaurant Process) \text{CRP(Chinese Restaurant Process)} CRP(Chinese Restaurant Process)来自动检测语义组件(例如关系中的子含义): π r , n ∼ C P R ( β ) \pi_{r,n}\sim CPR(\beta) πr,n∼CPR(β);
- 利用正态分布 h ∼ N ( u h , σ h 2 I ) \textbf{h}\sim\mathcal{N}(\textbf{u}_h,\sigma_h^2\textbf{I}) h∼N(uh,σh2I)获取头实体嵌入;
- 利用正态分布 t ∼ N ( u t , σ t 2 I ) \textbf{t}\sim\mathcal{N}(\textbf{u}_t,\sigma_t^2\textbf{I}) t∼N(ut,σt2I)获取尾实体嵌入;
- 构造关系嵌入向量 u r , n = t-h ∼ N ( u t − u h , ( σ h 2 + σ t 2 ) I ) \textbf{u}_{r,n}=\textbf{t-h}\sim\mathcal{N}(\textbf{u}_t-\textbf{u}_h,(\sigma_h^2+\sigma_t^2)\textbf{I}) ur,n=t-h∼N(ut−uh,(σh2+σt2)I);
其中, u \textbf{u} u是嵌入向量的均值, σ \sigma σ是方差。最终的评分函数是
E ( h , r , t ) ∝ ∑ n = 1 N r π r , n N ( u t − u h , ( σ h 2 + σ t 2 ) I ) \mathcal{E}(h,r,t)\propto \sum_{n=1}^{N_r}\pi_{r,n}\mathcal{N}(\textbf{u}_t-\textbf{u}_h,(\sigma_h^2+\sigma_t^2)\textbf{I}) E(h,r,t)∝n=1∑Nrπr,nN(ut−uh,(σh2+σt2)I)
其中, N r N_r Nr是 r r r语义组件的数量, π r , n \pi_{r,n} πr,n是由 CRP \text{CRP} CRP生成的第 i i i个组件的权重。
引用文献
[1]. Zhiyuan Liu, Yankai Lin and Maosong SUn. Representation Learning for Natural Language Processing.