用广搜和动态规划写个路径规划程序

GitHub项目地址：https://github.com/HarmoniaLeo/Search-Map

设计内容要求

在生活中常常遇到需要得出从一个起点出发，在最短的路程内经过所有目的地的方案。比如，在货运物流和邮政当中，需要得出一辆运货载具从发货点出发，经过所有目的地的最短路程，以便节约成本；对于一个景区，往往需要向游客提供一次性游览所有景点的最短线路，从而让游客有最佳的游览体验。

然而，常规导航软件只能得出两个点之间的最短路径，远远无法达到我们的要求。正因如此，旨在解决实际地图上连接多点的最短路径问题的多点最短路径规划系统的研发显得尤为重要。

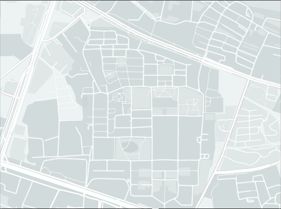
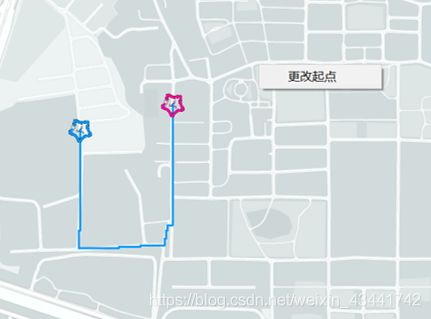
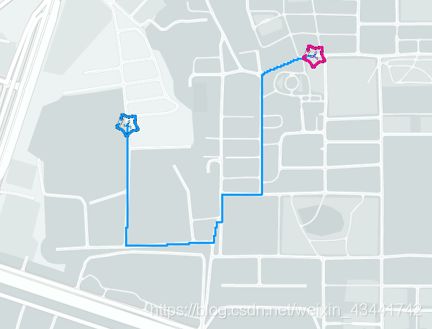
本软件便实现了在真实世界地图的基础上，对于用户给出的起点和若干个目标点，生成最短路径并在真实世界地图上绘出的功能。

设计步骤和原理

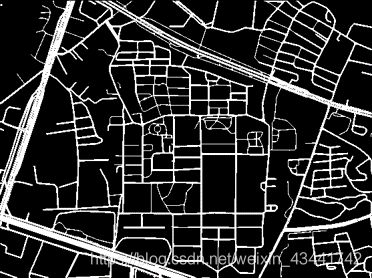
1. 地图二值化
   首先使用OpenCv库，读取被拖入的行政区划图每个像素点的色彩信息，针对被拖入的行政区划图进行“非0即255”的二值化，将底图转化为黑白图像，其中白色的部分被作为可以通行的道路，黑色的部分则是障碍物。

   在这种情况下，整张地图就可以被存为一个bool型的二维数组，用于之后的广度优先搜索。
   二值化前的图像
   二值化后的图像

2. 添加起点和目标点
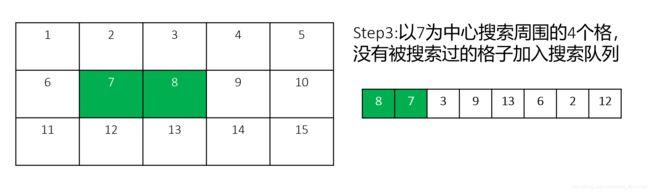
   因为不能把点添加在不可通过的位置，所以每次添加点时均要用广度优先搜索找到指定位置附近最近的可通过位置。
   在添加目标点的时候，还需要从目标点开始利用广度优先搜索寻找地图上其他的点，连接路径并用二维数组（边矩阵）储存地图上任意两点之间的路径，包括经过的像素以及长度，以用于之后的动态规划寻找最佳路径。
   每次添加点，都从起点开始使用动态规划法规划连接所有点的最短路径，并把经过的所有像素在地图上标注出来。

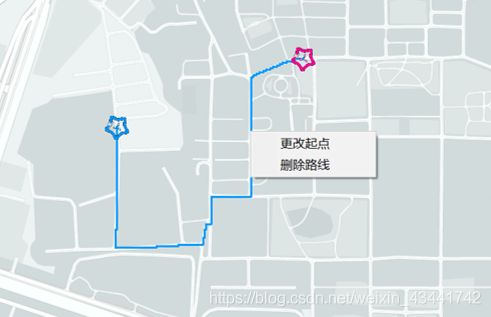
3. 删除目标点
   删除有关目标点的信息，包括边矩阵当中从目标点连出连向其他点的所有边，和其他点连向目标点的边，重新从起点开始使用动态规划法规划连接所有点的最短路径。

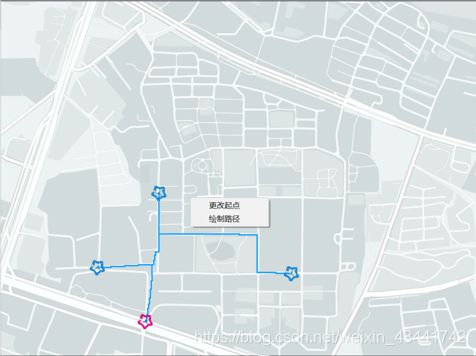
4. 动态展示路径
   绘制每条路径时加入分段绘制功能，每次调用时只绘制一部分像素点。通过按顺序每间隔一小段时间绘制起点、目标点以及连接它们的路径来完成路径的动态展示。

算法讲解

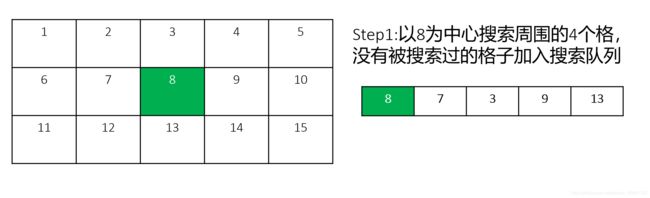
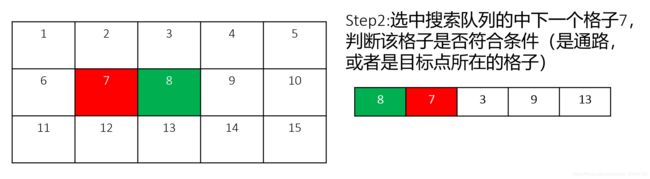
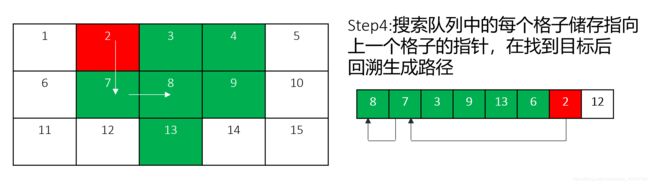
1. 广度优先搜索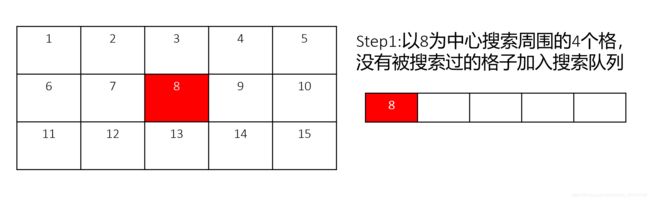

2. 动态规划解TSP问题

部分图片转载自博客：https://www.cnblogs.com/dddyyy/p/10084673.html

2.1 TSP问题介绍

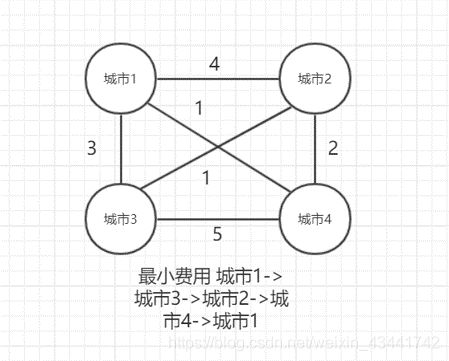
一个售货员必须访问n个城市，这n个城市是一个完全图，售货员需要恰好访问所有城市的一次，并且回到最终的城市，城市于城市之间有一个旅行费用，售货员希望旅行费用之和最少。

• 完全图：完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。
  

2.2 分支定界法

把所有的解列出来，形成一棵树，利用剪枝深度优先进行遍历（DFS），遍历的过程记录和寻找最优解

• 剪枝就是把一条再深搜下去也不是最优解的分支剪去。若当前正在搜索的分支深度已经大于目前最小深度，则该分支一定不是最优解

一定程度上解决了问题，但复杂度高，为o(n!)

2.3 动态规划法

将原问题拆分为子问题，原问题的解为所有子问题解的最优解。

原问题：从城市1出发经过[2,3,4]这几个城市，再回到城市1，使总花费最少
子问题：
从1出发，到2，然后再从2出发，经过[3,4]这几个城市，然后回到1，使得花费最少
从1出发，到3，然后再从3出发，经过[2,4]这几个城市，然后回到1，使得花费最少
从1出发，到4，然后再从4出发，经过[2,3]这几个城市，然后回到1，使得花费最少

运用递推，得出状态转移方程：
$$dp[1][\{2,3,4\}]=min\{D_{12}+dp[2][\{3,4\}]，D_{13}+dp[3][\{2,4\}]，D_{14}+dp[4][\{2,3\}]\}$$

对于第一个子问题，有子子问题：
从2出发，到3，然后再从3出发，经过[4]这几个城市，然后回到1，使得花费最少
从2出发，到3，然后再从3出发，经过[4]这几个城市，然后回到1，使得花费最少

运用递推，得出状态转移方程：
$$dp[2][\{3,4\}]=min\{D_{23}+dp[3][\{4\}]D_{24}+dp[4][\{3\}]\}$$

用二维数组表示该状态转移方程，就可以利用循环打表的方式得出结果：

用二进制来表示横坐标上的数值。例如{2,3,4}表示为111，{2,3}表示为110

从右下到左上循环打表：

for(int i=0;pow(2,i)<=8(111);i++)
	for(int j=4;j>1;j--)
		if(pow(2,j)&i==1)//枚举的起点包含在已经经过的城市中
			continue;//该位置值不存在
		else 从先前情况中推出该位置值;

从先前情况中推出该位置值：

for (int p = 0; pow(2, p) <= i; p++)//p用于枚举已经经过的城市
	if (p == j||pow(2,p)&i==0)  continue;//p不能与起点相同，且p枚举的城市必须已经经过
	else 
		如果本次枚举值小于该位置值，则更新该位置值：
		dp[j][i]=D[j][p]+D[p][i-pow(2,p)] 

表格最左上的值便是该TSP问题最优解，枚举起点的时间复杂度为o(n)枚举已经经过城市所有情况的时间复杂度为$o(2^n)$，枚举已经经过的城市的时间复杂度为o(n)，总时间复杂度为$o(n^2\cdot 2^n)$

本问题由于不需要回到起点，实际情况比标准TSP问题更为复杂，需要分别枚举起点和终点，建立状态转移矩阵dp[i][k][j]来求解，时间复杂度为$o(n^3\cdot 2^n)$

其中i代表起点，j代表终点，k代表经过的城市的二进制状态，i’表示第二个点

状态转移方程为：
$$dp[i[k][j]=mindp[i][0][i’]+dp[i’][k-pow(2,j)][j]$$
dp[n][0][m]：初始状态，表示从n到m期间一个点都没经过，也就是m到n的边权
min{dp[0][111……1-pow(2,终点)][终点]}：所求的结果

状态转移矩阵的每个位置可以追溯其起点和终点，但同时也要记录第二个点，也就是起点与到已经过城市状态的接口。得出路径采用递推的策略，从0开始，先将0设为当前点，枚举第二个点，将当前点加入路径，再将第二个点设为当前点，枚举第二个点，以此类推，直到找不到第二个点时，将终点加入路径。

软件使用说明

1. 初始化
   将任意bmp地图拖入对话框，完成软件初始化。

2. 添加起点：
   鼠标右键菜单中选择添加起点命令。
   
   

3. 添加目标点：
   鼠标左键点击地图上的一个位置。
   

4. 删除目标点：
   右击图片上有目标点的位置弹出右键菜单，选择删除目标点命令。
   
   

5. 更改起点：
   在地图上一点处右击，弹出右键菜单，选择更改起点。
   
   

6. 删除路线：
   右击图片上有路线的位置弹出右键菜单，选择删除路线命令，则所有点和边都会被删除。
   

7. 动态展示路线：
   右击图片上无路径的位置弹出右键菜单，选择绘制路径命令，则会开始路线的动态展示。